Sudoku

Z Wikipedii

Sudoku (jap. 数独, sūdoku; od sūji wa dokushin ni kagiru, czyli cyfry muszą być pojedyncze) – łamigłówka, której celem jest wypełnienie diagramu 9x9 w taki sposób, aby w każdym wierszu, w każdej kolumnie i w każdym dziewięciopolowym kwadracie 3x3 znalazło się po jednej cyfrze od 1 do 9.

Zasady przypominają trochę kwadrat łaciński, wymyślony i badany przez średniowiecznych matematyków z terenów Arabii (XIII wiek). W Sudoku, w przeciwieństwie do kwadratu łacińskiego, cyfry nie mogą się powtarzać nie tylko w żadnym wierszu i kolumnie, ale także w małym kwadracie 3x3.

W obecnej postaci Sudoku stało się popularne na świecie dzięki dołączaniu go do wielu gazet.

Spis treści 1 Historia 2 Metody rozwiązywania 2.1 Metoda 1 2.2 Metoda 2 2.3 Metoda 3 3 Odmiany 4 Popularność w mediach 5 Mistrzostwa Polski i świata w sudoku 6 Liczba możliwych plansz 7 Zobacz też 8 Linki zewnętrzne 9 Przypisy

[edytuj] Historia

Łamigłówka przeszła wiele mutacji. Dzisiejsze sudoku pojawiło się po raz pierwszy w Japonii w 1986 roku, jednak międzynarodową sławę zyskało dopiero w 2005 roku.

[edytuj] Metody rozwiązywania

W przeciwieństwie do innych łamigłówek sudoku nie wymaga od gracza wykonywania żadnych rachunków matematycznych, dzięki czemu wydaje się banalna. W rzeczywistości bez cierpliwości oraz umiejętności logicznego myślenia rozwiązanie diagramu nie jest możliwe.

Do diagramu cyfry wpisywać należy jedynie w miejsca, gdzie cyfra na pewno powinna się znajdować. Niepewne miejsca można tylko zanotować lub zaznaczyć, by uniknąć kreślenia i poprawek.

Poniżej przedstawione są podstawowe metody rozwiązywania Sudoku:

[edytuj] Metoda 1

Polega na znajdowaniu miejsca, gdzie w obrębie małego kwadratu 3x3 pasuje dana cyfra na zasadzie eliminacji rzędów i kolumn, w których ta cyfra znajduje się w innych kwadratach.

Diagram 1 - cyfrę 4 wpisać można tylko w jedno pole środkowego dolnego kwadratu (oba pozostałe rzędy są już zajęte).

Diagram 2 - bardziej skomplikowany przypadek, znalezienie miejsca dla cyfry 3. Cyfra 3 pasuje w dwa miejsca w środkowym dolnym kwadracie. Pozwala to na wyeliminowanie tego rzędu (cyfra 3 musi znaleźć się w tym rzędzie, niezależnie czy na polu po lewej czy po prawej), więc w prawym dolnym kwadracie dwa rzędy są zajęte. Jedną kolumnę zajmuje wpisana już cyfra 3, więc pozostaje jedyne pole gdzie można wpisać cyfrę 3.(to obok 8)

Diagram 1

Diagram 2

[edytuj] Metoda 2

Polega na dopełnianiu rzędu, kolumny lub kwadratu 3x3 cyframi od 1 do 9.

Diagram 3 - w dolnym rzędzie brakuje już tylko dwóch cyfr, Łatwo sprawdzić, że są to 1 i 7. Do drugiego pustego pola od lewej pasuje tylko cyfra 1, ponieważ w tej kolumnie już znajduje się cyfra 7. Cyfra 7 natomiast powinna się znaleźć w pierwszym pustym polu po lewej.

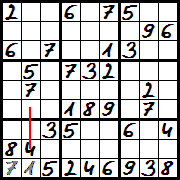
Diagram 4 - w pewnym momencie można dopełnić cały kwadrat, dla przykładu lewy dolny. Cyfra 2 pasuje tylko do środkowej kolumny, cyfra 6 tylko do środkowego rzędu. Do tego gdzie umiejscowić cyfrę 9 można w tym przypadku dojść na dwa sposoby:

• bo jest to ostatnia cyfra jaka pozostała do wpisania w tym kwadracie
• bo nie można tam wpisać ani cyfry 2 ani cyfry 6

Diagram 3

Diagram 4

[edytuj] Metoda 3

Jest to metoda wymagająca "bazgrania" po diagramie. Polega ona na stawianiu w odpowiednim miejscu kratki kropek-podpowiedzi. Kropki stawia się tak, by jasno określić cyfrę - patrz Diagram 5.

Diagram 5

Diagram 6 - rozwiązując Sudoku często spotykamy się z sytuacją, kiedy w kwadracie 3x3 dana cyfra może znaleźć się dokładnie w dwóch miejscach. Zaznaczamy wtedy oba te miejsca kropką, postawioną w odpowiednim punkcie kratki.

Diagram 7 i 8 - kiedy później, w trakcie rozwiązywania, jedno z tych miejsc zostanie zapełnione jakąś cyfrą inną niż wskazuje kropka, to w drugie miejsce można automatycznie wpisać cyfrę wskazaną przez kropkę.

Diagram 6

Diagram 7

Diagram 8

[edytuj] Odmiany

Istnieją również inne odmiany sudoku:

• Sudoku samurai składa się z pięciu kwadratów połączonych ze sobą w kształcie litery X
• W sudoku diagonalnym cyfry nie mogą się powtarzać również po przekątnych kwadratu.
• Sudoku trójwymiarowe, w kształcie kostki sześciennej o wymiarach 9x9x9
• Killer Sudoku - początkowa plansza nie ma żadnych wpisanych cyfr, ale zamiast tego ma zaznaczone obszary obejmujące od 2 do 7 pól, dla których podana jest suma cyfr zawartych w nich.
• W sudoku magnetycznym niedozwolone jest stykanie się rogami takich samych cyfr.
• Sudoku na większej planszy, z większą liczbą symboli (np. plansza 12×12 podzielona na prostokąty 3×4 i 12 różnych symboli do rozmieszczenia, plansza 16x16 podzielona na 16 kwadratów po 16 liczb do rozmieszczenia).

[edytuj] Popularność w mediach

W 2004 oraz 2005 r. sudoku stało się niezwykle popularne w Wielkiej Brytanii dzięki publikacjom łamigłówki w tamtejszych gazetach. Modę na sudoku zapoczątkował „The Times” 12 grudnia 2004 r. W Polsce sudoku (pod obecną nazwą) jako pierwszy opublikował tygodnik „Polityka” (15 czerwca 2005 r.), kolejne były „Angora”, „Przyjaciółka” , „Gazeta Wyborcza”, „Przegląd”, „Wiedza i Życie” oraz „Obrazki logiczne”. Gra ta jednak ukazywała się już wcześniej w polskiej prasie m.in. w „Wiedzy i Życiu” pod nazwą „Dziewięć na dziewięć”.

[edytuj] Mistrzostwa Polski i świata w sudoku

Pierwsze mistrzostwa Polski w sudoku, zorganizowane przez tygodnik „Polityka”, zakończyły się 5 listopada 2005 roku. Zwycięzcą został Michał Karwański, tytuł I wicemistrza zdobył Łukasz Bożykowski, a II wicemistrza Katarzyna Ślósarczyk.

Tytuł pierwszego mistrza świata w sudoku zdobyła we włoskim miasteczku Lucca w 2006 r. Jana Tylová z Czech.

[edytuj] Liczba możliwych plansz

W 2005 matematycy Bertram Felgenhauer z Politechniki w Dreźnie oraz Frazer Jarvis z Uniwersytetu w Sheffield udowodnili, że istnieje 6 670 903 752 021 072 936 960 (słownie - sześć tryliardów sześćset siedemdziesiąt trylionów dziewięćset trzy biliardy siedemset pięćdziesiąt dwa biliony dwadzieścia jeden miliardów siedemdziesiąt dwa miliony dziewięćset trzydzieści sześć tysięcy dziewięćset sześćdziesiąt) różnych poprawnych plansz sudoku. Po utożsamieniu wersji różniących się permutacją cyfr, wierszy, lub kolumn, oraz powstałych przez odbicia i obroty, pozostaje 1 472 730 538 plansz.^[1]

[edytuj] Zobacz też

Kakuro

[edytuj] Linki zewnętrzne

• James F. Crook. A Pencil-and-Paper Algorithm for Solving Sudoku Puzzles. „Notices of the AMS”. Volume 56, Number 4 (4 2009) (en). [dostęp 24 marca 2009].  – algorytm rozwiązania dowolnego sudoku (w języku angielskim)

[edytuj] Przypisy

1. ↑ Źródło: Muy interesante, kwiecień 2007, Madryt, str. 106