Zjawisko Halla
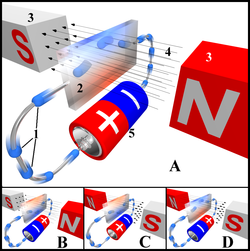
1. elektrony, 2. element Halla, 3. magnesy, 4. pole magnetyczne, 5. źródło zasilania
Zjawisko Halla, efekt Halla – zjawisko fizyczne polegające na wystąpieniu różnicy potencjałów w przewodniku, w którym płynie prąd elektryczny, gdy przewodnik znajduje się w poprzecznym do płynącego prądu polu magnetycznym. Ta różnica potencjałów, zwana napięciem Halla, pojawia się między płaszczyznami ograniczającymi przewodnik, prostopadle do płaszczyzny wyznaczanej przez kierunek prądu i wektor indukcji magnetycznej[1]. Jest ona spowodowana działaniem siły Lorentza na ładunki poruszające się w polu magnetycznym.
Zjawisko zostało odkryte w 1879 roku przez Edwina Halla (wówczas doktoranta).
Wyprowadzenie[edytuj | edytuj kod]
Niech przewodnik będzie prostopadłościanem o bokach Jeśli wzdłuż przewodnika (równolegle do ) płynie prąd o natężeniu (nadając nośnikom prądu prędkość unoszenia ), zaś prostopadle do powierzchni przewodnika (równolegle do ) skierowane jest pole magnetyczne o indukcji to na nośniki prądu o ładunku w kierunku działa siła Lorentza:
odchylając te ładunki do jednej ze ścianek. W ten sposób między tą ścianką a ścianką do niej przeciwną wytwarza się różnica gęstości ładunków, a więc i pole elektryczne o natężeniu które może być wyrażone przez różnicę potencjałów. Na kolejne nośniki zatem działa także siła kulombowska. Wypadkowa siła jest równa:
W stanie równowagi, kiedy siła Lorentza i kulombowska się równoważą, zachodzi równanie:
lub
gdzie:
- – koncentracja nośników,
- – ładunek nośnika prądu (elektrony lub dziury),
- – grubość płytki, wymiar w kierunku pola magnetycznego,
- – natężenie prądu,
- – stała zależna od materiału (tzw. stała Halla),
- – wartość indukcji magnetycznej.
Napięcie powstałe pomiędzy ściankami przewodnika, nazywane jest napięciem Halla.
Stałą Halla wyraża się przeważnie przez m³/C, Ω·cm/Gs lub jednostkach pokrewnych.
Detekcja[edytuj | edytuj kod]
W materiałach wytwarzających niewielkie napięcie Halla, rzędu 10 μV, do jego pomiaru stosuje się metody pośrednie. Przykładowo, badany materiał umieszcza się w stałym polu magnetycznym i podłącza do źródła prądu zmiennego. Prąd ten, płynący wzdłuż próbki, wywołuje powstanie zmiennego napięcia Halla między brzegami próbki w kierunku poprzecznym. Ma ono taką samą częstotliwość jak prąd podłużny. Napięcie to wzmacnia się wzmacniaczem selektywnym i bada detektorem fazoczułym, który porównuje fazę napięcia Halla z fazą prądu podłużnego i rejestruje jedynie prąd o fazie zgodnej z prądem podłużnym[2].
Zjawiska analogiczne[edytuj | edytuj kod]
Pod nazwą efektu Halla kryją się również inne zjawiska o analogicznych skutkach (czyli gromadzenie ładunku na krawędziach próbki), lecz o zasadniczo różnych przyczynach fizycznych. Mówi się zatem o tzw. anomalnym efekcie Halla, w którym napięcie Halla jest proporcjonalne do namagnesowania próbki magnetycznej, przez którą płynie prąd. Znany jest również tzw. spinowy efekt Halla, w którym nie pojawia się elektryczne napięcie Halla, ale na krawędziach próbki akumulują się nośniki o dwóch różnych kierunkach spinu. Mechanizm tego zjawiska nie jest do końca poznany.
Efekty towarzyszące[edytuj | edytuj kod]
Przy wyprowadzaniu wzoru na napięcie Halla dla uproszczenia założono, że wszystkie elektrony mają tę samą prędkość. W rzeczywistości prędkości elektronów w ciele stałym mają pewien rozkład, który w przewodniku opisuje statystyka Fermiego-Diraca (w półprzewodniku można przybliżyć ten rozkład rozkładem Maxwella-Boltzmanna). Oznacza to, że część elektronów ma prędkość większą, a część mniejszą od średniej. Na szybsze, a więc bardziej energetyczne elektrony, większy wpływ ma siła Lorentza (w węższym znaczeniu – tylko oddziaływanie magnetyczne), na wolniejsze siła Coulomba. To powoduje, że szybsze i wolniejsze elektrony są odchylane ku przeciwnym końcom ciała w kierunku poprzecznym do kierunku prądu. Obecność bardziej energetycznych elektronów powoduje wzrost temperatury w tym obszarze ciała. To oznacza powstanie gradientu temperatury i dyfuzję elektronów od końca cieplejszego do chłodniejszego. To sprawia, że rzeczywiste napięcie Halla jest mniejsze od wyliczonego – jest to tak zwane zjawisko Ettingshausena.
Zastosowanie[edytuj | edytuj kod]
Efekt Halla umożliwia pomiar znaku ładunków poruszających się w przewodniku oraz ich koncentrację.
Dla znanych materiałów pomiar napięcia Halla pozwala określić wartość indukcji pola magnetycznego. Przyrządy wykorzystujące efekt Halla do pomiaru tej indukcji nazywają się hallotronami. Są one powszechnie wykorzystywane w różnych czujnikach, na przykład ABS, ESP, padach do gier[3].
Zjawisko Halla jest również podstawą działania silnika Halla.
Przypisy[edytuj | edytuj kod]
- ↑ Halla zjawisko, [w:] Encyklopedia PWN [dostęp 2021-07-22].
- ↑ Metody doświadczalne w fizyce ciała stałego. Praca zbiorowa pod red. Mieczysława Subotowicza. Lublin: Uniwersytet Marii Curie-Skłodowskiej, Wydział Matematyki, Fizyki i Chemii, Zakład Fizyki Doświadczalnej, 1976, s. ?.
- ↑ Efekt Halla w padach do gier - koniec z dryfowaniem [online], www.it-manuals.info, 20 marca 2023 [dostęp 2023-07-26] (pol.).


















