Prawo Hardy’ego-Weinberga
Prawo Hardy’ego-Weinberga – prawo określające stosunki pomiędzy frekwencją alleli a częstością genotypów w populacji oraz warunki, w jakich stosunki te będą zachowane.
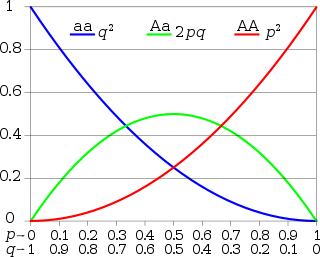
Proporcje genotypów w populacji spełniającej założenia prawa Hardy’ego-Weinberga określa się jako rozkład Hardy’ego-Weinberga (dla genu z dwoma allelami proporcje te odpowiadają rozwinięciu kwadratu sumy frekwencji alleli). Gdy genotypy w określonym locus występują z częstościami przewidzianymi na podstawie tego prawa, mówimy, że locus (gen) jest w równowadze Hardy’ego-Weinberga.
Prawo zostało sformułowane przez matematyka Godfreya H. Hardy’ego i, niezależnie od niego, przez lekarza Wilhelma Weinberga[1]. Prawo, sformułowane początkowo dla pojedynczego locus dwuallelicznego, można uogólnić dla wielu loci, dla loci wieloallelicznych oraz systemów poliploidalnych. Prawo stanowi jeden z fundamentów teorii genetyki populacji organizmów płciowych. Ma duże znaczenie dla zrozumienia procesu ewolucji i związanych z nim zmian częstości alleli i genotypów w populacjach.
Definicja
[edytuj | edytuj kod]
Jeżeli populacja mendlowska spełnia określone, podane niżej założenia, i w danym locus – w którym dwa allele, i występują z częstościami odpowiednio i to:
1) częstość alleli w populacji nie zmienia się z pokolenia na pokolenie,
2) częstość genotypów zależy tylko od częstości alleli genów i ustala się w kolejnych pokoleniach, niezależnie od początkowej częstości genotypów, w proporcjach odpowiadających rozwinięciu dwumianu gdzie odpowiada częstości homozygot – częstości heterozygot a – częstości homozygot
Proporcję tę (dla locus z dwoma allelami – ) określa się mianem rozkładu Hardy’ego-Weinberga częstości genotypów. Gdy genotypy w danym locus występują z częstościami przewidzianymi przez rozkład Hardy’ego-Weinberga, to locus znajduje się w równowadze Hardy’ego-Weinberga[3][4].
Założenia prawa Hardy’ego-Weinberga
[edytuj | edytuj kod]Częstości alleli i genotypów w populacji będą kształtować się zgodnie z przewidywaniami prawa Hardy’ego-Weinberga, jeżeli[5][6]:
- osobniki w populacji są diploidalne,
- osobniki rozmnażają się wyłącznie płciowo (z wykorzystaniem męskich i żeńskich gamet),
- pokolenia nie zachodzą na siebie,
- kojarzenia w populacji są losowe (panmiksja),
- liczebność populacji jest nieskończenie wielka,
- nie ma migracji,
- nie zachodzą mutacje,
- nie działa dobór naturalny.
Konsekwencje niespełnienia założeń
[edytuj | edytuj kod]Jeżeli któreś z wymienionych założeń nie jest spełnione, frekwencje alleli i genotypów będą odbiegać od przewidywanych. Zależnie od tego, które z założeń jest niespełnione, wpływ na frekwencje alleli i genotypów jest odmienny.
Prawo Hardy’ego-Weinberga ma zastosowanie do populacji mendlowskich, czyli takich, które rozmnażają się płciowo, produkując gamety męskie i żeńskie, w związku z czym materiał genetycznych tworzących je osobników składa się na wspólną pulę genową. Jeżeli w populacji osobniki rozmnażają się bezpłciowo, klonalnie, każdy z klonów (ramet) jest izolowany płciowo i nie dochodzi do mieszania genów, a więc częstości genotypów nie osiągną równowagi H-W[7].
Całkowicie losowe kojarzenie pomiędzy osobnikami (panmiksja) oznacza, że prawdopodobieństwo skojarzenia się dowolnego osobnika z dowolnym osobnikiem płci przeciwnej jest takie samo. W rezultacie np. osobniki podobne do siebie pod względem cech fenotypowych czy genetycznych nie mają tendencji do częstszego kojarzenia się wzajemnie w pary niż z osobnikami odmiennymi, podobnie osobniki zasiedlające jeden płat siedliska nie kojarzą się częściej ze sobą niż z osobnikami w innym płacie siedliska[8]. Jeżeli kojarzenia w populacji nie są losowe (np. wskutek chowu wsobnego), częstości genotypów w kolejnych pokoleniach będą odbiegać od przewidywanych na podstawie prawa Hardy’ego-Weinberga – w przypadku chowu wsobnego następuje wzrost homozygotyczności w populacji[9].
Prawo H-W jest w pełni spełnione tylko dla populacji o bardzo dużej liczbie osobników, teoretycznie bliskiej nieskończoności, jednak w praktyce już populacja licząca powyżej kilkuset osobników może znajdować się w równowadze H-W. Im mniejsza liczebność osobników w populacji, tym większy wpływ na kształtowanie frekwencji alleli i genotypów będą miały zdarzenia losowe (zob. dryf genetyczny, ewolucja neutralna) zmieniające zarówno częstości alleli, jak i genotypów[8].
Jeżeli osobniki populacji różnią się względem siebie pod względem rozrodczości lub przeżywalności, to niektóre genotypy (i allele) będą częściej eliminowane lub będą zostawiały mniej potomstwa niż inne, w rezultacie ich udział w populacji zmaleje (efekt działania doboru naturalnego), co wpłynie na zmianę frekwencji alleli i genotypów w następnych pokoleniach[6].
Brak imigracji oznacza, że do populacji nie dostają się osobniki z innych populacji, w których występują inne allele lub w których frekwencje alleli są inne, ani też osobniki o różnych genotypach nie różnią się od siebie pod względem tendencji do emigrowania z populacji, ponieważ taki przepływ genów może zmienić częstości alleli i genotypów w rozważanej populacji[8][10].
Prawo H-W zakłada, że w opisywanej teoretycznie populacji geny nie mutują z jednego w allelu w drugi ani nie powstają nowe allele, bo z definicji zmienia to ich częstości występowania. Presja mutacyjna jest słabą siłą ewolucyjną, w niewielkim tylko stopniu wpływającą na częstości alleli w populacjach i na równowagę H-W[6][11].
W sytuacji, gdy nie jest spełnione więcej niż jedno z założeń dotyczących mutacji, doboru, migracji, wielkości populacji, ich sumaryczny wpływ na częstości genotypów w populacji może się równoważyć, wówczas proporcje genotypów w populacji mogą (choć nie muszą) pozostawać w zgodzie z przewidywaniami prawa H-W[6].
Przykład: locus MN u człowieka
[edytuj | edytuj kod]W populacji ludzkiej istnieje zmienność białek występujących na powierzchni erytrocytów. Jedno z takich białek jest kodowane przez locus MN. W badaniach elektroforetycznych można wyróżnić dwa allele występujące w tym locus (M i N) oraz trzy genotypy (MM, MN, NN). Badając grupy krwi u osób zamieszkujących Wielką Brytanię Race i Sanger (1975) stwierdzili, że wśród przebadanych 1000 osób grupę krwi M (genotyp MM) miało 298, grupę krwi MN (genotyp MN) – 489, i 213 miało grupę krwi N (genotyp NN). Aby sprawdzić, czy badany locus jest w równowadze H-W należy:
1) obliczyć częstości alleli w próbie:
- częstość allelu M: [a],
- częstość allelu N:
2) obliczyć częstości genotypów przewidywane na podstawie prawa H-W (przyjmując obserwowane w próbce częstości alleli za reprezentatywne dla populacji):
- częstość genotypu MM:
- częstość genotypu MN:
- częstość genotypu NN:
Ponieważ wielkość próby wynosi 1000 osobników, oczekiwane na podstawie prawa H-W ilości osobników o tych genotypach wynoszą odpowiednio MM = 294,3; MN = 496,4; NN = 209,3.
| Genotyp | Suma | |||
| MM | MN | NN | ||
| Obserwowana liczebność | 298 | 489 | 213 | 1000 |
| Obserwowana częstość genotypów | 0,298 | 0,489 | 0,213 | 1 |
| Oczekiwana częstość genotypów (na podstawie rozkładu H-W) |
0,2943 | 0,4964 | 0,2093 | 1 |
| Oczekiwana liczebność (częstość oczekiwana×liczebność próby) |
294,3 | 496,4 | 209,3 | – |
3) sprawdzić za pomocą testu statystycznego, czy nie ma istotnych różnic między obserwowanymi i przewidywanymi liczebnościami poszczególnych genotypów (zob. też Weryfikacja hipotez statystycznych). Najłatwiej uczynić to można za pomocą testu chi-kwadrat. Statystykę tego testu oblicza się ze wzoru:
gdzie:
- – liczba osobników o danym genotypie stwierdzonych w próbie,
- – liczba osobników o danym genotypie oczekiwanych, w tym przypadku na podstawie prawa H-W.
Liczba stopni swobody (df) dla testu chi-kwadrat wynosi
- df = (ilość klas obiektów w danych) – (ilość parametrów) – 1,
w danym przypadku df = 3 – 1 – 1 = 1. Na podstawie statystyki i liczby stopni swobody z tablic statystycznych odczytuje się wartość, określającą prawdopodobieństwo odrzucenia hipotezy zakładającej brak różnic pomiędzy porównywanymi rozkładami liczebności genotypów. W tym przypadku dla i df = 1 wynosi ono P = 0,67. Ponieważ jest ono większe niż krytyczna wartość prawdopodobieństwa oznacza to, że hipotezy o braku różnic pomiędzy obserwowanymi i oczekiwanymi liczebnościami genotypów nie można odrzucić (niewielkie różnice są wynikiem przypadku). Stąd wniosek, że ten locus w populacji brytyjskiej jest w równowadze H-W[12].
Wyprowadzenie
[edytuj | edytuj kod]Sposób Hardy’ego
[edytuj | edytuj kod]Oto jaki sposób argumentowania zastosował G.H. Hardy:
Z wielką niechęcią wtrącam się do dyskusji na tematy, w których nie jestem ekspertem, tym bardziej że spodziewam się, że pewne moje proste spostrzeżenia, które chciałbym ogłosić, powinny być już znane biologom. Jednakże pewne stwierdzenia Pana Udny Yule’go, na które zwrócił moją uwagę Pan R.C. Punnett, sugerują, że mimo wszystko zaprezentowanie mych uwag może być korzystne. (...) Załóżmy, że to para jednostek dziedziczenia (alleli), z których jest dominujące, i że w każdej generacji liczebność dominujących fenotypów heterozygot i fenotypów recesywnych pozostaje w proporcji Dodatkowo, załóżmy że liczebności są wystarczająco duże, tak że kojarzenia są losowe, że płci są równo reprezentowane pomiędzy fenotypami, i że wszystkie są równie płodne. Prosta matematyczna operacja, w postaci tabelki mnożenia wystarczy, aby zrozumieć, że w następnym pokoleniu liczebności osobników będą wynosiły co opiszmy jako Interesujące pytanie brzmi: w jakich okolicznościach taki rozkład pozostanie taki sam, jak w poprzednim pokoleniu? Łatwo stwierdzić, że będzie tak wtedy, gdy jest równe A skoro jest równe niezależnie od tego, jakie będą liczebności i rozkład liczebności pozostanie niezmieniony w następnych pokoleniach
Krok po kroku
[edytuj | edytuj kod]Podręcznikowy sposób wyprowadzenia zależności opisanej prawem H-W wygląda tak[c][14][4]:
Niech częstości genotypów
w diploidalnej populacji rozmnażającej się płciowo, gdzie kojarzenia są losowe, wynoszą początkowo (w pokoleniu ) odpowiednio:
a częstości alleli i odpowiednio i
tak więc:
a
i w rezultacie
Prawdopodobieństwo kojarzenia pomiędzy samicą i samcem dowolnego genotypu jest równe iloczynowi częstości genotypów reprezentowanych przez danego samca i samicę. Ponieważ krzyżówki między genotypami mogą zachodzić w obu kierunkach, częstości kojarzeń (i powstałych w ich wyniku genotypów potomstwa) wynoszą:
| Kojarzenie | Prawdopodobieństwo kojarzenia | Częstość genotypów potomstwa | ||
| – | – | |||
| [d] | – | |||
| [d] | – | – | ||
| [d] | – | |||
| – | – | |||
W rezultacie częstość każdego genotypu w potomstwie (pokolenie ) wynosi:
Jak widać, w kolejnym pokoleniu częstości alleli nie zmieniły się i dalej wynoszą i tak jak w pokoleniu a częstości genotypów zależą tylko od częstości alleli i w następnym pokoleniu nie ulegną już zmianie[4].
Sposób graficzny
[edytuj | edytuj kod]
Zależność pomiędzy częstościami alleli i genotypów w populacji, postulowaną przez prawo Hardy’ego-Weinberga można też wyprowadzić graficznie – z wykorzystaniem kwadratu (szachownicy) Punnetta[4].
Komentarz
[edytuj | edytuj kod]Warto zauważyć, że w gruncie rzeczy obliczenia te rozwijają jedynie prawidłowości, które wynikają z praw Mendla, i w podobnych postaciach, choć w mniej ogólny sposób (tzn. tylko dla konkretnych wartości częstości alleli lub genotypów) były formułowane wcześniej także przez innych naukowców: G.U. Yule’a, K. Pearsona, W.E. Castle’a[e], S. Wrighta[15][16]. To, co wyróżnia sformułowanie problemu przez Hardy’ego i Weinberga, to, oprócz formalnego dowodu, który jest w gruncie rzeczy trywialny, zwrócenie uwagi na warunki, jakie muszą być spełnione (założenia prawa), żeby częstości alleli i genotypów w populacji nie zmieniały się w kolejnych pokoleniach[16]. Weinberg ponadto pokazał, że prawo to funkcjonuje także w odniesieniu do więcej niż dwóch alleli (pomimo tego, że nie miał pojęcia o tym, czy takie wieloalleliczne układy istnieją) oraz że w takich przypadkach dojście do stanu równowagi nie będzie natychmiastowe (tj. w następnym pokoleniu), ale asymptotyczne (nastąpi po wielu pokoleniach)[1][15].
Uogólnienie modelu
[edytuj | edytuj kod]Prawo Hardy’ego-Weinberga można uogólnić dla więcej niż dwóch alleli i więcej niż jednego locus. W przypadku trzech alleli w populacji będzie występować sześć genotypów, których częstości w stanie równowagi będą odpowiadać rozwinięciu trójmianu do kwadratu [17]. Natomiast, jeszcze bardziej ogólnie, dla alleli, przyjmując, że allele występują z częstościami częstości poszczególnych genotypów wyrażać się będą kolejnymi wyrazami rozwinięcia kwadratu wielomianu:
co daje dla wszystkich homozygot:
i dla wszystkich heterozygot:
Prawo H-W może być również zastosowane do opisu zmian częstości genotypów w systemach poliploidalnych. Dla przypadku jednego locus, w którym występuje -różnych alleli częstości genotypów w równowadze H-W w populacji poliploidów odpowiadają rozwinięciu wielomianu:
gdzie określa ploidię (np. dla organizmów tetraploidalnych )[f][18][19].
Zastosowanie
[edytuj | edytuj kod]
W codziennej praktyce badaczy
[edytuj | edytuj kod]Prawo Hardy’ego-Weinberga stosuje się w badaniach genetyki populacji albo do oszacowania częstości genotypów w populacji na podstawie częstości alleli z próby, albo sprawdzając odchylenia obserwowanych częstości genotypów od częstości oczekiwanych, obliczonych na podstawie częstości alleli, przy założeniu, że populacja jest w równowadze[21]. To, czy odchylenie jest znaczące, testuje się za pomocą testów statystycznych ( test Fishera) lub z wykorzystaniem metod MCMC. Ze względu na relatywnie duże prawdopodobieństwo popełnienia błędu pierwszego rodzaju przy stosowaniu testu opracowano nowe narzędzia do testowania tego, czy populacja znajduje się w stanie równowagi H-W[22]. Testy takie dostępne są w internecie[23] i w pakietach oprogramowania służących do analiz genetyki populacyjnej[24].
Przykład: Oszacowanie częstości nosicieli fenyloketonurii
[edytuj | edytuj kod]Fenyloketonuria jest chorobą metaboliczną o podłożu genetycznym (autosomalną recesywną) – choroba rozwija się u homozygot z uszkodzonymi obydwiema kopiami genu hydroksylazy fenyloalaninowej (PAH). Występuje z częstością 1:7000 – 1:8000 osób w populacji zamieszkującej Polskę[25][26]. Znając tę częstość i zakładając, że locus odpowiedzialne za tę chorobę jest w równowadze H-W, można oszacować na podstawie prawa H-W, jaką część populacji stanowią heterozygoty – nosiciele genu odpowiedzialnego za tę chorobę, u których choroba nie rozwija się w związku z obecnością jednej nieuszkodzonej kopii genu. Skoro 1 chory przypada na 8000 zdrowych: to częstość genu odpowiedzialnego za chorobę w populacji polskiej wynosi ponieważ to Stąd częstość heterozygot – zdrowych nosicieli, wynosi (1:46). Szacuje się, że jedna na 46 osób zdrowych w populacji polskiej jest nosicielem uszkodzonej kopii genu PAH[25].
Ograniczenia zastosowania
[edytuj | edytuj kod]- Należy pamiętać, że frekwencje genów położonych na chromosomach płciowych mogą kształtować się inaczej niż genów na autosomach. Załóżmy, że gen jest sprzężony z płcią. Wówczas płeć heterogametyczna (np. samce u ssaków, samice u ptaków) ma jedną kopię genu (w związku z tym nazywana jest też hemizygotą), a płeć homogametyczna ma dwie kopie. Częstości genotypów w stanie równowagi będą wynosić i u płci heterogametycznej, i i u płci homogametycznej. Dobrym przykładem jest częstość występowania daltonizmu u poszczególnych płci w populacji ludzkiej. Daltonizm jest warunkowany przez recesywny gen sprzężony z chromosomem X. Przypadłość ta dotyczy 1 na 12 mężczyzn w Europie Zachodniej i 1 na 200 kobiet (0,005, co jest bliskie teoretycznej wartości )[27][28].
- Jeżeli proporcje alleli u obydwu płci różnią się, to do osiągnięcia równowagi nie dojdzie w następnym pokoleniu. Tym niemniej u potomków proporcje alleli wyrównają się u obydwu płci, i w kolejnym pokoleniu można się spodziewać osiągnięcia równowagi H-W (w przypadku locus z dwoma allelami)[29].
- W przypadku wielu loci dojście do stanu równowagi może nastąpić później niż w następnym pokoleniu.
- W przypadku loci sprzężonych (położonych blisko siebie na chromosomie) do osiągnięcia stanu równowagi potrzeba większej liczby pokoleń. W przypadku sprzężenia absolutnego równowaga nie będzie możliwa do osiągnięcia[30].
- W niektórych przypadkach allele heterozygoty segregują do gamet w proporcjach innych niż 1:1, co jest określane jako odchylenie mejotyczne (mejotic drive). Wówczas częstości genotypów będą odbiegać od przewidywanych na podstawie prawa H-W[4].
- Prawo H-W opisuje populacje z pokoleniami nie zachodzącymi na siebie (takimi, w których po wydaniu potomstwa rodzice giną). W stanach równowagi, gdy nie zmienia się częstość alleli, prawo będzie spełnione także w populacjach z pokoleniami zachodzącymi na siebie, gdy organizmy dają potomstwo kilka razy w swoim życiu. Jednak jeżeli częstość alleli z jakichś powodów uległa zmianie, nowy stan równowagi osiągnięty zostanie, dopiero gdy wymrze ostatni osobnik z poprzedniego pokolenia[17].
- Z rozważań teoretycznych wynika, że w pewnych specyficznych warunkach, dla szczególnych wartości częstości genotypów, równowaga H-W może być zachowana również wtedy, gdy kojarzenia w populacji nie są losowe (taką sytuację określono mianem kojarzenia pseudo-losowego) – a więc założenie o losowych kojarzeniach jest warunkiem wystarczającym, ale nie koniecznym dla zachowania rozkładu H-W[31][32].
Znaczenie
[edytuj | edytuj kod]Hardy, podsumowując swoje osiągnięcia jako czystego matematyka, stwierdził przekornie, że w swojej karierze nie zrobił nic, z czego mogłaby wynikać jakaś praktyczna korzyść („Nothing I have ever done is of the slightest practical use”)[33]. W rzeczywistości trudno o przykład prawa mającego większe konsekwencje praktyczne, niż prawo nazwane jego imieniem. Z prawa tego wynika, że, przy określonych warunkach, częstości genotypów w populacji mogą być przewidziane na podstawie częstości alleli, w rezultacie analizy mogą być przeprowadzone na podstawie częstości alleli, a nie częstości genotypów[21]. W gruncie rzeczy całe badanie ewolucji genetycznej sprowadza się do zadawania pytań, co się stanie, gdy jedno lub więcej z założeń prawa H-W nie będzie spełnione, i identyfikowanie przyczyn powodujących odchylenia w obserwowanych częstościach genotypów od przewidywanych na podstawie prawa H-W[6].
Prawo Hardy’ego-Weinberga stanowi fundament teorii genetyki populacji organizmów rozmnażających się płciowo[4][34]. Bezpośrednio zainspirowało J.B.S. Haldane’a, R.A. Fishera i S. Wrighta w ich badaniach nad relacjami pomiędzy doborem naturalnym a genetyką populacji (które doprowadziły do nowoczesnej syntezy darwinowskiej)[16]. Odkrycie praw Mendla i ich rozwinięcia w postaci prawa Hardy’ego-Weiberga wyeliminowało zarzuty wobec teorii ewolucji drogą doboru naturalnego wiążące się z przekonaniem, że mieszanie się u potomstwa cech rodziców powoduje nieuchronny spadek zmienności i uśrednianie cech[35]. Wykorzystywane jest do teoretycznych badań wpływu doboru naturalnego i innych czynników powodujących ewolucję na częstości alleli i genotypów oraz przewidywania zmian tych częstości w populacjach w naturze. Np. jeżeli jakaś populacja nie znajduje się w stanie równowagi H-W, można na tej podstawie wnioskować, że jeżeli czynnik powodujący to odchylenie przestanie działać, to w następnym pokoleniu losowe kojarzenie usunie to odstępstwo; jeżeli nastąpi mutacja, to powinna ona pozostawać w populacji w swej początkowej, niskiej częstości[4]. Prawo H-W przyniosło wyjaśnienie m.in. mechanizmów powodujących utrzymywanie w populacji ukrytej zmienności genetycznej, powodujących negatywne populacyjne efekty chowu wsobnego, stanowiło punkt wyjścia do zidentyfikowania roli przypadku i wielkości populacji dla trwałości populacji[36]. W oparciu o prawo H-W opracowano m.in. miary nasilenia kojarzeń krewniaczych w populacji (współczynnik wsobności)[37], zróżnicowania genetycznego wewnątrz- i międzypopulacyjnego (współczynnik Fst)[38], do prawa H-W odwołują się metody szacowania wielkości nierównowagi gametycznej[39] oraz siły doboru[40][41] i dryfu genetycznego[42][43].
Historia odkrycia
[edytuj | edytuj kod]Mimo ponownego „odkrycia” zapomnianych praw Mendla na początku XX wieku wielu uczonych długo pozostawało sceptycznymi wobec nich. Argumentowano na przykład, że częstość alleli dominujących zawsze będzie wzrastać w populacji. Udny Yule podczas dyskusji po wykładzie Reginalda Punnetta na forum Epidemiological Section of the Royal Society of Medicine in London w roku 1908, krytykując „szkołę mendlowską”, stwierdził, że jeśli brachydaktylia u ludzi jest determinowana przez gen dominujący i nie ma innych czynników wpływających na jej występowanie, to można się spodziewać, że będzie występować z częstością 3:1, a przecież tak nie jest. Punnett opacznie zrozumiał błędne spostrzeżenie Yule’a i uznał, że jego oponent utrzymuje, że w populacji brachydaktylia powinna się rozpowszechnić („why the nation was not slowly becoming brachydactylous” zamiast „in the course of time one would expect that in the absence of counteracting factors, to get three brachydactylous persons to one normal”)[15][16]. Punnett, który uważał, że jest to argumentacja błędna, ale nie potrafił wskazać, na czym polega błąd, zwrócił się o pomoc do swojego kolegi – matematyka Godfrey H. Hardy’ego, z którym zapoznał się podczas wspólnych meczów w krykieta. Hardy, zawołany matematyk, rozstrzygnięcie tego problemu nurtującego biologów uznał, jak się wyraził, za „bardzo proste”[15]. Do roku 1943 w świecie anglojęzycznym prawo to zwane było prawem Hardy’ego, podczas gdy publikacja Weinberga pozostawała nieznana wśród anglojęzycznych genetyków. Wówczas Stern w swoim artykule[44] zwrócił uwagę na to, że w tym samym roku, w którym opublikował swój artykuł Hardy, niemiecki lekarz Wilhelm Weinberg opublikował w niemieckojęzycznym czasopiśmie pracę, w której niezależnie od Hardy’ego sformułował i udowodnił podobne wnioski. Stern zaproponował, by prawo to nazwać prawem Hardy’ego-Weinberga. Dlatego od 1943 roku nazwa tego prawa honoruje obydwu jego odkrywców[44].
Anegdoty i komentarze
[edytuj | edytuj kod]Od lat 80. XX wieku Genetics Society of America w swoim czasopiśmie „Genetics” w okrągłe rocznice opublikowania prac, w których przedstawiono prawo H-W, zamieszcza artykuły prezentujące biogramy odkrywców prawa, tło historyczne tego odkrycia oraz komentarze i anegdoty z nimi związane[15][16][45].
Historyk nauki Edwards znajduje wielką ironię w fakcie, że do rozwiązania tak prostego problemu trzeba było zaangażować tak znakomitego matematyka, jakim był Hardy[16].
Z kolei J.F. Crow zwraca uwagę na bariery językowe, które spowodowały, że przez blisko 35 lat praca Weinberga pozostawała niezauważona przez anglojęzycznych genetyków, i ze smutkiem zauważa, że w owym czasie anglojęzyczni naukowcy ignorowali publikacje zawierające ważne naukowe odkrycia tylko dlatego, że były publikowane w językach innych niż angielski – taki był los genetycznych odkryć Mendla, Weinberga i G. Malécota (przy czym ten ostatni publikował nie w języku niemieckim, tylko we francuskim)[15].
Jedną ze spraw intrygujących ludzi zainteresowanych historią nauki jest to, dlaczego tak ważna dla biologii praca Hardy’ego, uznanego angielskiego uczonego, została opublikowana w amerykańskim czasopiśmie „Science”, a nie, w zdawałoby się bliższym, brytyjskim tygodniku „Nature”. Spekulowano, że wynikało to z tego, że Hardy chciał ukryć przed kolegami-matematykami w Anglii swe zaangażowanie w rozstrzyganie tak trywialnego problemu matematycznego. Jednakże z korespondencji przyjaciela Hardy’ego, Punnetta, wynika, że w rzeczywistości spowodowane to było negatywnym, czy wręcz wrogim, stosunkiem ówczesnych edytorów „Nature” do wszystkich koncepcji związanych z mendelizmem[16].
Uwagi
[edytuj | edytuj kod]- ↑ Ponieważ każdy osobnik miał dwa allele genu MN, cała próba zawiera 2000 kopii genu. Każda homozygota ma dwie jednakowe kopie genu, a heterozygota po jednym allelu M i N, stąd liczba alleli M w próbie wynosi 1085, alleli N – 915.
- ↑ Dla czterech równań (trzy opisujące częstości genotypów oraz ) i trzech niewiadomych zależność między nimi (warunek, który pokazał Hardy) wynika stąd: po przekształceniu dlatego
- ↑ W podobny sposób przeprowadził wywód Wilhelm Weinberg.
- ↑ a b c W związku z tym, że są 3 możliwe genotypy samic i 3 możliwe genotypy samców, w sumie możliwych jest 9 typów kojarzeń. Stąd częstości krzyżówek, w których genotypy samic i samców są różne, trzeba przemnożyć przez 2 (bo są dwa możliwe kierunki krzyżowania).
- ↑ Prawo H-W zwane jest też czasami prawem Hardy’ego-Weinberga-Castle’a.
- ↑ Rozkład genotypów w populacjach gatunków poliploidalnych nie zawsze musi stosować się do tych przewidywań, a to ze względu na skomplikowany system segregowania alleli do gamet u poliploidów, disomiczny, polisomiczny lub mieszany. Dlatego zastosowanie prawa H-W do obliczania częstości alleli i genotypów u poliploidów na podstawie fenotypów wymaga dobrej znajomości genetyki danego gatunku i zastosowania odpowiednio zmodyfikowanych modeli matematycznych.
Przypisy
[edytuj | edytuj kod]- ↑ a b Weinberg 1908 ↓.
- ↑ Krzanowska, Łomnicki i Rafiński 1982 ↓, s. 55–56.
- ↑ Krzanowska, Łomnicki i Rafiński 1982 ↓, s. 57.
- ↑ a b c d e f g Futuyma 2008 ↓, s. 197.
- ↑ Krzanowska, Łomnicki i Rafiński 1982 ↓, s. 60–62.
- ↑ a b c d e f Futuyma 2008 ↓, s. 198.
- ↑ Krzanowska, Łomnicki i Rafiński 1982 ↓, s. 52.
- ↑ a b c Krzanowska, Łomnicki i Rafiński 1982 ↓, s. 53.
- ↑ Futuyma 2008 ↓, s. 199.
- ↑ Felsenstein 2005 ↓, s. 4–21.
- ↑ Krzanowska, Łomnicki i Rafiński 1982 ↓, s. 87.
- ↑ a b Hartl i Clark 1997 ↓, s. 80–82.
- ↑ Hardy 1908 ↓.
- ↑ Krzanowska, Łomnicki i Rafiński 1982 ↓, s. 53–57.
- ↑ a b c d e f Crow 1999 ↓.
- ↑ a b c d e f g Edwards 2008 ↓.
- ↑ a b Krzanowska, Łomnicki i Rafiński 1982 ↓, s. 61.
- ↑ De Silva i in. 2005 ↓.
- ↑ Luo 2006 ↓.
- ↑ Krzanowska, Łomnicki i Rafiński 1982 ↓, s. 58.
- ↑ a b Felsenstein 2005 ↓, s. 6, 25–27.
- ↑ Wigginton 2005 ↓.
- ↑ Kalkulator równowagi Hardy’ego-Weinberga ↓.
- ↑ Peakall i Smouse 2012 ↓.
- ↑ a b Jarochowicz i Mazur 2007 ↓.
- ↑ Sendecka i Cabalska ↓.
- ↑ Wong 2010 ↓.
- ↑ Mandall 2010 ↓.
- ↑ Felsenstein 2005 ↓, s. 12–14.
- ↑ Krzanowska, Łomnicki i Rafiński 1982 ↓, s. 66.
- ↑ Li 1988 ↓.
- ↑ Stark 2005 ↓.
- ↑ Hardy G.H. 1940. A Mathematician’s Apology. Cambridge University Press, Cambridge, przekład na j. polski (M. Fedyszak).
- ↑ Krzanowska, Łomnicki i Rafiński 1982 ↓, s. 60.
- ↑ Adam Łomnicki. Spotkanie teorii Darwina z genetyką. „Kosmos. Problemy nauk biologicznych”. 58 (3–4 (284–285)), s. 315–317, 2009. Polskie Towarzystwo Przyrodników im. Mikołaja Kopernika.
- ↑ Futuyma 2008 ↓, s. 199–204, 228.
- ↑ Futuyma 2008 ↓, s. 200.
- ↑ Futuyma 2008 ↓, s. 205.
- ↑ Futuyma 2008 ↓, s. 207–208.
- ↑ Futuyma 2008 ↓, s. 275–280.
- ↑ Krzanowska, Łomnicki i Rafiński 1982 ↓, s. 67–82.
- ↑ Futuyma 2008 ↓, s. 228–233.
- ↑ Krzanowska, Łomnicki i Rafiński 1982 ↓, s. 101–106.
- ↑ a b Stern 1943 ↓.
- ↑ Crow 1988 ↓.
Bibliografia
[edytuj | edytuj kod]- J.F. Crow. Hardy, Weinberg and language impediments. „Genetics”. 152 (3), s. 821–825, 1999. [zarchiwizowane z adresu 2015-09-24]. (ang.).
- H.N. De Silva, A.J. Hall, E. Rikkerink, M.A. McNeilage i inni. Estimation of allele frequencies in polyploids under certain patterns of inheritance. „Heredity”. 95, s. 327–334, 2005.
- A.W.F. Edwards. G.H. Hardy (1908) and Hardy-Weinberg Equilibrium. „Genetics”. 179, s. 1143–1150, 2008.
- J. Felsenstein: Theoretical evolutionary genetics. [w:] Felsenstein Genome 562 course [on-line]. University of Washington, Seattle, USA, 2005. s. 393. [dostęp 2014-11-02]. (ang.).
- D.J. Futuyma: Ewolucja. Wyd. 1. Warszawa: Wydawnictwa Uniwersytetu Warszawskiego, 2008, s. 606. ISBN 978-83-235-0577-8.
- G.H. Hardy. Mendelian Proportions in a Mixed Population. „Science”. 28/706, s. 49–50, 1908. (ang.).
- D.L. Hartl, A.G. Clark: Principles of Population Genetics. Sunderland, Massachusetts. USA: Sinauer Associates, 1997, s. 542. ISBN 0-87893-306-9.
- S. Jarochowicz, A. Mazur. Fenyloketonuria – choroba metaboliczna uwarunkowana genetycznie. „Przegl. Med. Uniw. Rzesz.”. 1, s. 76–90, 2007.
- H. Krzanowska, A. Łomnicki, J. Rafiński: Wprowadzenie do genetyki populacji. Warszawa: PWN, 1982. ISBN 83-01-02225-6.
- C.C. Li. Pseudo-random mating populations. In celebration of the 80th anniversary of the Hardy-Weinberg law. „Genetics”. 119, s. 731–737, 1988.
- Z.W. Luo, Modeling population genetic data in autotetraploid species, Ze Zhang i inni, „Genetics”, 172, 2006, s. 639–646, DOI: 10.1534/genetics.105.044974.
- Ananya Mandall: Color Blindness Prevalence.. Health, 2010. [dostęp 2014-04-15]. (ang.).
- E. Sendecka, B. Cabalska: Fenyloketonuria. [w:] Klinika Pediatrii, Instytut Matki i Dziecka [on-line]. [dostęp 2014-11-02].
- A.E. Stark. On extending the Hardy-Weinberg law. „Gen. Mol. Biol.”. 28 (3), s. 485, 2005.
- Curt Stern. The Hardy–Weinberg law. „Science”. 97(2510), s. 137–138, 1943. DOI: 10.1126/science.97.2510.137. (ang.).
- W. Weinberg. Über den Nachweis der Vererbung beim Menschen. „Jahreshefte des Vereins für vaterländische Naturkunde in Württemberg”. 64, s. 368–382, 1908.
- J.E. Wigginton, D.J. Cutler, G.R. Abecasis. A note on exact tests of Hardy-Weinberg equilibrium. „Am. J. Hum. Genet.”. 76, s. 887–893, 2005.
- B. Wong. Points of View: Color Blindness. „Nature Methods”. 7, s. 775, 2010. DOI: 10.1038/nmeth1010-775a. (ang.).
Linki zewnętrzne
[edytuj | edytuj kod]- Santiago Rodriguez, Tom R. Gaunt, Ian N.M. Day: Kalkulator równowagi Hardy’ego-Weinberga. [dostęp 2014-02-03]. [zarchiwizowane z tego adresu (2017-10-08)]. (ang.).
- R. Peakall, P.E. Smouse: GeneAlEx – Genetic Analyses in Excel. 2012. [dostęp 2014-02-05]. [zarchiwizowane z tego adresu (2013-04-24)]. (ang.).
- Wigginton et al.: Składnia języków Fortran/C/C++/R/PERL dla testów na równowagę Hardy’ego-Weinberga. 2005. [dostęp 2014-11-02]. (ang.).
- Prawo Hardy’ego-Weinberga na Youtube. Centrum Fizyki Teoretycznej PAN, opowiada Alicja Puścian z Instytutu Biologii Doświadczalnej im. M. Nenckiego PAN, 2005. [dostęp 2014-11-02].















































































![{\displaystyle f_{t+1}(\mathrm {A} _{1}\mathrm {A} _{1})=f_{t}(\mathrm {A} _{1}\mathrm {A} _{1})^{2}+f_{t}(\mathrm {A} _{1}\mathrm {A} _{1})\times f_{t}(\mathrm {A} _{1}\mathrm {A} _{2})+f_{t}(\mathrm {A} _{2}\mathrm {A} _{2})^{2}/4=[f_{t}(\mathrm {A} _{1}\mathrm {A} _{1})+f_{t}(\mathrm {A} _{1}\mathrm {A} _{2})/2]^{2}=p_{t}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fa8396b7911fb2f857d412d6d7feb36df1aa213)
![{\displaystyle f_{t+1}(\mathrm {A} _{1}\mathrm {A} _{2})=f_{t}(\mathrm {A} _{1}\mathrm {A} _{1})\times f_{t}(\mathrm {A} _{1}\mathrm {A} _{2})+2f_{t}(\mathrm {A} _{1}\mathrm {A} _{1})\times f_{t}(\mathrm {A} _{2}\mathrm {A} _{2})+f_{t}(\mathrm {A} _{1}\mathrm {A} _{2})^{2}/2+f_{t}(\mathrm {A} _{1}\mathrm {A} _{2})\times f_{t}(\mathrm {A} _{2}\mathrm {A} _{2})=2[(f_{t}(\mathrm {A} _{1}\mathrm {A} _{1})+f_{t}(\mathrm {A} _{1}\mathrm {A} _{2})/2)\times (f_{t}(\mathrm {A} _{1}\mathrm {A} _{2})/2+f_{t}(\mathrm {A} _{2}\mathrm {A} _{2}))]=2p_{t}q_{t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d8161d5eac0e14d1beada62a9ca9fd493243a6b)
![{\displaystyle f_{t+1}(\mathrm {A} _{2}\mathrm {A} _{2})=f_{t}(\mathrm {A} _{2}\mathrm {A} _{2})^{2}/4+f_{t}(\mathrm {A} _{1}\mathrm {A} _{2})\times f_{t}(\mathrm {A} _{2}\mathrm {A} _{2})+f_{t}(\mathrm {A} _{2}\mathrm {A} _{2})^{2}=[f_{t}(\mathrm {A} _{1}\mathrm {A} _{2})/2+f_{t}(\mathrm {A} _{2}\mathrm {A} _{2})]^{2}=q_{t}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c2e355a50737d8663accddac13eddfefd2546e8)

































