Zbiór Mandelbrota

Zbiór Mandelbrota

Zbiór Mandelbrota

Przybliżone samopodobieństwo zbioru Mandelbrota

Zbiór Mandelbrota (żuk Mandelbrota) - podzbiór płaszczyzny zespolonej, którego brzeg jest jednym ze sławniejszych fraktali. Nazwa tego obiektu została wprowadzona dla uhonorowania jego odkrywcy, francuskiego matematyka Benoit Mandelbrota.

Konstrukcja

Zbiór tworzą te punkty $p \in \mathbb{C}$ dla których ciąg opisany równaniem rekurencyjnym:

$\left\{\begin{matrix} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! z_{0} = 0\\ z_{n+1} = z_{n}^{2} + p \end{matrix}\right.$

nie dąży do nieskończoności:

$\lim _{n \to \infty} z_{n} \not = \infty$

Można wykazać, że jest to równoważne z:

$\forall_{n \in \mathbb{N}} |z_{n}|<2$

Podsumowując jednym zdaniem:

$M = \{p \in \mathbb{C}: \forall_{n \in \mathbb{N}} |z_n|<2 \}$

Alternatywnie zbiór Mandelbrota definiuje się jako punkty, które w rodzinie zbiorów Julii dają zbiory spójne.

Obrazy przybliżone

Przybliżony (128 pierwszych wyrazów ciągu) obraz zbioru (czarny)

Dokładniejszy obraz (2048 pierwszych wyrazów ciągu)

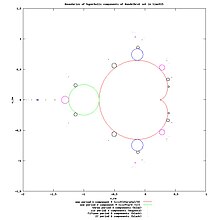
Za pomocą komputera można wykreślić przybliżone obrazy zbioru Mandelbrota. Obrazy takie przedstawiają zamieszczone rysunki.

Aby uzyskać taki obraz dla każdego punktu $p$ oblicza się pewną liczbę początkowych wyrazów ciągu $z_n$. Decyduje się, że punkt należy do zbioru jeżeli dla wszystkich (w szczególności dla ostatniego) wyrazów tego podciągu spełniony jest warunek $|z_n|<2$. Jest to tym samym obraz przybliżony. Okazuje się jednak, że efekt przybliżenia jest widoczny tylko w dużych powiększeniach. Zbiór Mandelbrota zawiera się (jest podzbiorem) każdego przybliżenia. Dla każdego z punktów nie należących do zbioru można określić liczbę $m$:

$\forall_{n \leqslant m} |z_{n}|<2$

Jest to liczba początkowych wyrazów ciągu $z_n$, które spełniają powyższy warunek. Ponieważ podczas wyznaczania obrazu przybliżonego liczba $m$ jest uzyskiwana niejako "za darmo", często wykorzystuje się ją do zabarwiania punktów nie należących do zbioru Mandelbrota. Każdej z wartości $m$ przyporządkowuje się pewien kolor.

Brzeg składowych zbioru Mandelbrota dla okresów 1-6

Punkty centralne składowych zbioru Mandelbrota dla okresów 1-8

Przykładowy program

Skrypt napisany w Matlabie generujący zbiór Mandelbrota podobny jak na górze strony:

%Zbiór Mandelbrota
 
%zakres układu współrzędnych:
x_min = -2.5;
x_max = 1.5;
y_max = 1.25;
y_min = -1.25;
 
iterations = 50;
m = input('podaj szerokość:\n'); %program wygeneruje obrazek o szerokości m pikseli i proporcji zależnej od zakresu układu wsp.
n = floor(m * (y_max - y_min)/(x_max - x_min));
unit = (x_max - x_min)/m;
Mal = zeros(n,m,3);
 
C_0 = x_min + 1i*y_max;
C = C_0;
 
%Tutaj zaczynają się parametry kolorowania
w1 = 50;
w2 = 50;
w3 = 50;
 
p1 = 2.2;
p2 = 2.2;
p3 = 2.2;
 
c1 = 1/4;
c2 = 1/2;
c3 = 3/4;
 
f1 = @(x) exp(-w1*abs(x-c1).^p1);
f2 = @(x) exp(-w2*abs(x-c2).^p2);
f3 = @(x) exp(-w3*abs(x-c3).^p3);
%koniec kolorowania
 
for i = 1:n
    C = C - real(C) + real(C_0);
    for j = 1:m
        c = checkC(0, C, iterations) / iterations;
        Mal(i,j,1) = f1(c);
        Mal(i,j,2) = f2(c);
        Mal(i,j,3) = f3(c);
        %Mal(i,j,:) = c; %gdy chcemy zbiór czarno biały
        C = C + unit;
    end
    C = C - 1i*unit;
end
 
imshow(Mal);

Użyta w skrypcie funkcja sprawdzająca zbieżność ciągu:

function [ it_used ] = checkC(z_0, C, it_max )
 
    for i = 0:it_max
        z_1 = z_0^2 + C;
        if abs(z_1) >= 2
            break;
        end
        z_0 = z_1;
    end
 
    it_used = i;
end

Zobacz też

• fraktal
• MPSolve - obliczanie punktów centralnych składowych zbioru Mandelbrota
• Mnich Mandelbrota
• zbiór Julii
• płonący statek

Linki zewnętrzne

• Zbiór Mandelbrota (ang.) w encyklopedii MathWorld
• Galeria fraktali w serwisie fraktalny.net
• Fragment żuka Mandelbrota wyświetlony przy ograniczeniu do 500 iteracji lub 2000 iteracji.

• 
• 
•