Statystyka odpornościowa
Statystyka odpornościowa[1] lub odporne metody statystyczne[2] – gałąź statystyki, obejmująca metody projektowane pod kątem odporności na niewielkie odejście od założeń modelu (szczególnie występowanie obserwacji odstających) lub rezygnacji z niektórych założeń.
Wprowadzenie[edytuj | edytuj kod]
Klasyczne metody statystyczne w dużym stopniu polegają na założeniach, które nie zawsze są spełnione w praktyce. W szczególności często zakłada się, że dane mają rozkład normalny (choćby w przybliżeniu), lub próbka jest dostatecznie duża, aby dało się zastosować centralne twierdzenie graniczne do otrzymania rozkładu normalnego błędu estymatora.
Estymatory bazujące na rozkładzie normalnym lub wielowymiarowym rozkładzie normalnym (takie jak np. współczynniki regresji liniowej, współczynnik korelacji Pearsona, czy odchylenie standardowe) mają zwykle tę cechę, iż obserwacje bardziej oddalone od średniej są bardziej wpływowe, czyli wchodzą z większą wagą do wyniku. Ma to groźną konsekwencję: w przypadku obecności w danych obserwacji odstających, czyli np. pomyłek typu przesunięcie przecinka, nawet jedna taka obserwacja może zakłócić wynik analizy.
Ponadto normalność rozkładu jest zawsze tylko przybliżeniem – realne dane są zawsze skwantowane (dyskretne) i ograniczone, a tymczasem zgodnie z rozkładem normalnym każda liczba rzeczywista ma dodatnie prawdopodobieństwo wystąpienia, czyli rozkład ten przewiduje np. istnienie ludzi o ujemnym wzroście lub ujemną wielkość galaktyki. Naturalnie przybliżenie to jest często tak dobre, że mimo to opłaca się je wykorzystywać, czasem jednak dane wyraźnie różnią się od rozkładu normalnego i standardowe metody statystyczne mogą dawać wątpliwe wyniki.
Istnieją miary „odporności” (ang. robustness) danej metody na naruszenie założeń modelu. Najczęściej używane są punkt załamania (ang. breakdown point) i funkcja wpływu (ang. influence function), opisane dalej.
Spora część odpornych metod statystycznych zastępuje rozkład normalny z metod klasycznych, rozkładem Studenta z niewielką liczbą stopni swobody, czyli dużą skośnością (w praktyce wykorzystuje się rozkłady z 4-6 stopniami swobody), lub stosuje kombinację dwóch lub większej liczby rozkładów.
Przykład: prędkość światła[edytuj | edytuj kod]
Gelman z zespołem w Bayesian Data Analysis (2004) rozważali zbiór danych związany z pomiarami prędkości światła wykonanymi przez Simona Newcomba[3].
Choć rozkład większości obserwacji wygląda na mniej więcej normalny, są też dwie oczywiste obserwacje odstające. Te obserwacje mają duży wpływ na średnią przyciągając ją do siebie i odciągając od średniej pozostałych. W ten sposób jeśli użyjemy średniej jako miary położenia rozkładu, wynik będzie obciążony.
Rozkład średniej zgodnie z centralnym twierdzeniem granicznym zbiega do rozkładu normalnego wraz ze wzrostem liczebności próbki do nieskończoności. Obserwacje odstające mogą jednak sprawić, że rozkład średniej nie będzie normalny nawet dla bardzo dużych prób. Ponadto obserwacje odstające, jeśli stanowią pewien stały procent próby, mogą zmienić parametry granicznego rozkładu normalnego.
Estymacja położenia[edytuj | edytuj kod]
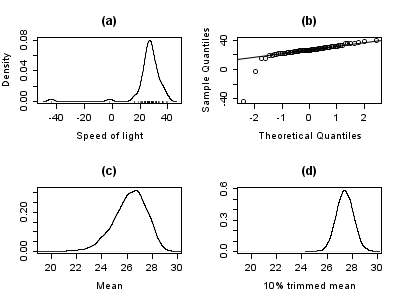
Wykresy poniżej przedstawiają gęstość prawdopodobieństwa dla rozkładu prędkości światła w danych (wykres (a)). Pokazany jest również wykres kwantylowo-kwantylowy. Obserwacje odstające są łatwe do zauważenia.
Wykresy (c) i (d) pokazują bootstrapowy rozkład średniej arytmetycznej (c) i średniej ucinanej w 10%. Średnia ucinana jest prostym odpornym estymatorem położenia, który bazuje na danych z odciętą częścią (tu 10%) skrajnych obserwacji, obliczając dla pozostałych zwykłą średnią arytmetyczną. Analiza była wykonana dla 10000-elementowej próby bootstrap, zarówno w przypadku średniej arytmetycznej, jak i uciętej.
Jak w oczywisty sposób wynika z wykresu, rozkład średniej jest szerzej rozrzucony (czyli ma większy błąd normalny) w przypadku średniej arytmetycznej. Co więcej rozkład średniej uciętej jest w przybliżeniu normalny, podczas gdy rozkład średniej arytmetycznej jest mocno skośny. W tej próbie 66 obserwacji tylko dwie obserwacje odstające sprawiły, że centralne twierdzenie graniczne nie daje się zastosować (wymagałoby o wiele większej liczby obserwacji).
Odporne metody statystyczne, których przykładem jest średnia ucinana, mają dawać lepsze od metod klasycznej statystyki rezultaty w sytuacjach występowania obserwacji odstających, lub ogólniej, gdy założenia modeli parametrycznych nie do końca są spełnione.
Chociaż średnia ucinana lepiej spisuje się w tym przykładzie od średniej arytmetycznej, istnieją jeszcze lepsze odporne estymatory. Średnia, mediana i średnia ucinana są szczególnymi przypadkami M-estymatorów, omówionych dalej w artykule.
Estymacja skali[edytuj | edytuj kod]
Obserwacje odstające w danych na temat prędkości światła wpłynęły nie tylko na średnią. Na ogół w celu estymacji skali (rozrzutu danego rozkładu wokół średniej) używane jest odchylenie standardowe, które jest w znacznie większym stopniu podatne na obserwacje odstające, ze względu na drugie potęgi we wzorze, które sprawiają, że obserwacje odstające są bardziej wpływowe.
Wykresy poniżej pokazują rozkład bootstrap odchylenia standardowego, odchylenia medianowego (MAD) i kwantylowego estymatora skali Qn (Rousseeuw i Croux, 1993). Wykresy opierają się na próbie bootstrap liczącej 10000 obserwacji, do której dodano pewien szum o rozkładzie normalnym (tzw. wygładzany bootstrap, ang. smoothed bootstrap). Wykres (a) pokazuje rozkład odchylenia standardowego, wykres (b) rozkład MAD, a wykres (c) rozkład Qn.
Rozkład odchylenia standardowego jest obciążony i rozproszony w wyniku obecności obserwacji odstających. MAD zachowuje się lepiej, a Qn jest nawet bardziej efektywne od MAD. Ten prosty przykład pokazuje, że w obecności obserwacji odstających odchylenie standardowe nie powinno być stosowane jako estymator skali.
Ręczne wyszukiwanie obserwacji odstających[edytuj | edytuj kod]
Tradycyjnie statystycy ręcznie wyszukiwali obserwacje odstające w danych i usuwali je, potwierdzając ewentualnie w źródle danych, czy faktycznie są to pomyłki. Faktycznie, w naszych danych o prędkości światła łatwo znaleźć dwie obserwacje odstające i usunąć je przed wykonaniem jakichkolwiek dalszych analiz. Jednakże w dzisiejszych czasach zbiory danych często składają się ze zbyt wielu zmiennych i obserwacji aby coś takiego było możliwe. Ponadto może pojawić się zarzut braku obiektywnych kryteriów takiego usuwania.
Jedne obserwacje odstające czasami maskują inne. Niech w zbiorze danych będzie jedna obserwacja odstająca, bardzo daleka od średniej i druga znacznie bliższa. Ponieważ obserwacja daleka zwiększy wartość odchylenia standardowego, więc bazując na odchyleniu nie zauważymy, że obserwacja bliższa także jest odstająca. Jeśli jednak usuniemy dalszą obserwację odstającą, wówczas odchylenie zmniejszy się i bliższa obserwacja odstająca stanie się łatwa do odróżnienia. Problem maskowania jest coraz bardziej dotkliwy, gdy zwiększa się złożoność danych.
Odporne metody statystyczne pozwalają na automatyczną detekcję obserwacji odstających, a następnie zmniejszenie ich wagi i oflagowanie lub usunięcie, w znaczący sposób upraszczając proces analizy.
Miary odporności[edytuj | edytuj kod]
Podstawowymi narzędziami używanymi do opisu i pomiaru odporności na obserwacje odstające, są punkt załamania (ang. breakdown point), funkcja wpływu (ang. influence function) i krzywa wrażliwości (ang. sensitivity curve).
Punkt załamania[edytuj | edytuj kod]
Intuicyjnie, punkt załamania estymatora jest proporcją niepoprawnych obserwacji (np. dowolnie dużych obserwacji odstających), które estymator jest w stanie wytrzymać, zanim zacznie dawać dowolnie duże wyniki. Na przykład mając próbę losową, czyli niezależnych zmiennych losowych i odpowiednie ich realizacje możemy użyć wzoru do estymacji średniej w populacji. Taki estymator ma punkt załamania zero, gdyż można uczynić średnią dowolnie dużą za pomocą zmiany jednej wartości
Im wyższy jest punkt załamania estymatora, tym bardziej estymator jest odporny. Punkt załamania nie może przekroczyć 50%, gdyż jeśli ponad połowa obserwacji jest wybranych z innej populacji, nie ma powodu aby traktować tę „inną” populację jako odstającą (obserwacje odstające z definicji stanowią mniejszość, w przeciwnym wypadku to reszta odstaje od nich). Istnieją estymatory, które osiągają ten maksymalny pułap (np. mediana ma punkt załamania równy 0.5). Średnia ucinana na poziomie X% (odcięte X% obserwacji z każdej strony rozkładu) ma punkt załamania X%[4].
Przykład: dane o prędkości światła[edytuj | edytuj kod]
W przykładzie prędkości światła, usunięcie dwóch najniższych wyników powoduje, że średnia wzrasta z 26.2 do 27.75 (zmiana o 1.55). Estymacja skali stworzona metodą Qn wynosi 6.3. Dzieląc to przez pierwiastek z wielkości próby możemy uzyskać odporny estymator błędu standardowego, wynoszący tutaj 0.78. Tak więc zmiana średniej związana z dwiema obserwacjami odstającymi jest tu prawie dwa razy większa od błędu standardowego.
Średnia ucinana na poziomie 10% wynosi tu 27.43. Usuwając dwie najmniejsze obserwacje uzyskujemy za jej pomocą 27.67 (zmiana o 0.24). Ewidentnie średnia ucinana jest mniej wrażliwa na obserwacje odstające, co wiąże się z jej wyższym punktem załamania.
Empiryczna funkcja wpływu[edytuj | edytuj kod]
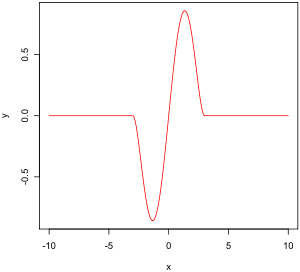
Empiryczna funkcja wpływu pokazuje, w jaki sposób estymator zachowuje się, gdy zmieniamy jedną obserwację w próbie i nie bierzemy pod uwagę ewentualnego pogwałcenia założeń modelu. Ilustracja przedstawia dwuwagową funkcję Tukeya pewnego dobrze zachowującego się estymatora.
Oznaczenia:
- to przestrzeń probabilistyczna,
- to przestrzeń mierzonych stanów
- to przestrzeń parametrów wymiaru
- to przestrzeń pomiarów
- to funkcja symbolizująca pomiar
- to zbiór wszystkich możliwych rozkładów na
Na przykład:
- to przestrzeń probabilistyczna
- jest zdefiniowana jako
Definicja empirycznej funkcji wpływu:
Niech i są niezależnymi zmiennymi losowymi o identycznym rozkładzie, a jest próbą statystyczną z tych zmiennych. jest estymatorem. Niech Empiryczna funkcja wpływu obserwacji jest zdefiniowana jako:
Funkcja ta pokazuje zatem zależność od wyników estymatora po zastąpieniu i-tej obserwacji przez
Funkcja wpływu i krzywa wrażliwości[edytuj | edytuj kod]
W drugim podejściu zamiast sprawdzać wpływ zmiany pojedynczej obserwacji na wynik estymacji, badany będzie wpływ punktowego zaburzenia na rozkład.
Niech będzie asymptotycznie nieobciążonym estymatorem pewnego parametru rozkładu spełniającego założenia modelu.
Niech będzie pewnym rozkładem który nie spełnia założeń modelu statystycznego, różni się jednak nieznacznie od
Wpływ na estymator przejścia z na jest wyrażony wzorem:
który jest pochodną kierunkową w punkcie w kierunku
Niech będzie miarą prawdopodobieństwa o masie 1 skupionej w punkcie Wybieramy Funkcja wpływu jest zdefiniowana przez:
Wzór ten opisuje wpływ infinitezymalnej zmiany w punkcie na poszukiwaną estymatę, standaryzowany masą zaburzenia (asymptotyczne obciążenie estymatora spowodowane przez zanieczyszczenie obserwacji).
Pożądane właściwości[edytuj | edytuj kod]
Właściwości funkcji wpływu, charakteryzujące najbardziej odporne estymatory:
- skończony punkt odrzucenia (ang. rejection point)
- mała maksymalna wrażliwość na błędy (ang. gross-error sensitivity)
- mała wrażliwość na lokalne przesunięcie (ang. local-shift sensitivity)
Punkt odrzucenia[edytuj | edytuj kod]
Maksymalna wrażliwość[edytuj | edytuj kod]
Wrażliwość na lokalne przesunięcia[edytuj | edytuj kod]
Ten wzór, podobny do definicji stałej Lipschitza, opisuje efekt przesunięcia obserwacji z punktu do pobliskiego punktu czyli innymi słowy dodania obserwacji w punkcie przy jednoczesnym usunięciu z
M-estymatory[edytuj | edytuj kod]
Powstało wiele rozmaitych podejść do konstrukcji odpornych estymatorów, w szczególności R-estymatory i L-estymatory. Obecnie tę dziedzinę zdominowały M-estymatory jako najbardziej ogólne, posiadające wysoki punkt załamania i wysoką efektywność (zobacz Huber (1981)).
M-estymatory są uogólnieniem estymatorów największej wiarygodności (MLE). Od MLE oczekujemy maksymalizacji prawdopodobieństwa czyli (równoważnie) minimalizacji W 1964 Huber zaproponował uogólnienie tego podejścia poprzez minimalizację wyrażenia gdzie jest pewną funkcją. MLE są tym samym szczególnym przypadkiem M-estymatorów. Nazwa ta pochodzi od ang. Maximum likelihood type estimators, czyli estymatory typu największej wiarygodności.
Minimalizacja często może być wykonana przez różniczkowanie i rozwiązanie równania gdzie oczywiście pod warunkiem, że jest różniczkowalne.
Zostało zaproponowanych wiele funkcji Wykresy poniżej pokazują cztery funkcje i odpowiadające im
Funkcja opisująca błąd kwadratowy rośnie coraz szybciej, podczas gdy dla błędów bezwzględnych rośnie liniowo. Stosując winsoryzację obserwujemy mieszaninę tych dwóch efektów: dla małych wartości x rośnie z kwadratem x, a kiedy zostanie osiągnięty określony próg (w przykładzie 1,5), wzrost staje się liniowy.
Funkcja Tukeya (ang. Tukey’s biweight) zachowuje się początkowo w podobny sposób, jak funkcja błędu kwadratowego, ale dla większych błędów staje się płaska.
Właściwości M-estymatorów[edytuj | edytuj kod]
Zostało pokazane, że M-estymatory mają asymptotycznie rozkład normalny, więc o ile można obliczyć ich błąd standardowy, dla dużych prób da się stosować metody wnioskowania statystycznego oparte na rozkładzie normalnym.
Dla małych prób ich rozkład może znacząco różnić się od normalnego, lepiej więc stosować inne metody wnioskowania statystycznego, jak bootstrap. Należy jednak ostrożnie projektować schematy badań bootstrap, aby nie przekroczyć (jakkolwiek wysokiego) punktu załamania estymatora.
Funkcja wpływu M-estymatora[edytuj | edytuj kod]
Można pokazać, że funkcja wpływu M-estymatora jest proporcjonalna do (Huber, 1981 (i 2004), s. 45), co oznacza, że właściwości takiego estymatora (takie jak jego punkt załamania, sumaryczną wrażliwość i wrażliwość na lokalne przesunięcie) można wyprowadzić znając jego funkcję
z danym przez:
Wybór i [edytuj | edytuj kod]
W wielu praktycznych sytuacjach wybór funkcji nie jest krytycznym warunkiem uzyskania dobrej odpornej estymaty, i wiele różnych funkcji da podobny odporny rezultat, znacząco lepszy w obecności obserwacji ostających od estymacji metodami klasycznymi (Huber, 1981).
Parametryczne estymatory odporne[edytuj | edytuj kod]
M-estymatory niekoniecznie są związane z funkcją gęstości i tym samym nie są rozwiązaniem w pełni parametrycznym. W pełni parametryczne podejście do odpornego modelowania i wnioskowania statystycznego, zarówno bayesowskiego, jak i największej wiarygodności, zwykle polega na zastosowaniu rozkładów takich jak rozkład t-Studenta z „ciężkimi ogonami”.
Dla rozkładu t Studenta z stopniami swobody, zachodzi:
Dla rozkład t sprowadza się do rozkładu Cauchy’ego. Liczba stopni swobody jest czasem nazywana parametrem kurtozy. Ten właśnie parametr steruje wielkością „ogonów” rozkładu. Generalnie, może być estymowany z próby jak każdy inny parametr. W praktyce jest to utrudnione, gdyż występuje wiele lokalnych maksimów gdy zezwolimy na zmienność Tak więc na ogół ustala się ten parametr sztywno na wartość w okolicach 4 lub 6. Wykres poniżej pokazuje, funkcję dla 4 różnych wartości
Przykład: prędkość światła[edytuj | edytuj kod]
Dla przykładu prędkości światła, uwalniając parametr kurtozy i maksymalizując wiarygodność, uzyskujemy:
Ustalając i maksymalizując wiarygodność, uzyskamy
Przypadki szczególne[edytuj | edytuj kod]
Jakkolwiek ten artykuł wiąże się z ogólnymi zasadami dotyczącymi jednowymiarowych metod statystycznych, dedykowane metody odporne istnieją dla problemów regresyjnych, GLM i estymacji parametrów różnych rozkładów.
Zobacz też[edytuj | edytuj kod]
Przypisy[edytuj | edytuj kod]
- ↑ Polska nazwa za dr. hab. Antonim L. Dawidowiczem ([1], s. 4) oraz słownikiem ISI.
- ↑ Elżbieta Pleszczyńska. Odporne metody statystyczne („Robust Statistics”). „Wiadomości statystyczne”. 1-12, s. 20, 1976. Główny Urząd Statystyczny.
- ↑ Dane te dostępne są wraz z materiałami uzupełniającymi książki Robust Regression and Outlier Detection (Rousseeuw i Leroy, 1986) na stronie Uniwersytetu w Kolonii.
- ↑ Huber (1981), Maronna et al (2006).
Bibliografia[edytuj | edytuj kod]
- Frank R. Hampel, Elvezio M. Ronchetti, Peter J. Rousseeuw, Werner A. Stahel: Robust Statistics – The Approach Based on Influence Functions. Wiley, 1986. (ponownie opublikowane w 2005 w miękich okładkach)
- Peter. J. Huber: Robust Statistics. Wiley, 1981. (ponownie opublikowane w 2004 w miękich okładkach)
- Peter J. Rousseeuw, Annick M. Leroy: Robust Regression and Outlier Detection. Wiley, 1987.(ponownie opublikowane w 2003 w miękich okładkach)
- Ricardo Maronna, Doug Martin, Victor Yohai: Robust Statistics – Theory and Methods. Wiley, 2006.
- Andrew Gelman, John B. Carlin, Hal S. Stern, Donald B. Rubin: Bayesian Data Analysis. Chapman & Hall/CRC, 2004.
- P.J. Rousseeuw, C. Croux. Alternatives to the Median Absolute Deviation. „Journal of the American Statistical Association”, s. 88, 1993.
Linki zewnętrzne[edytuj | edytuj kod]
- Justyna Majewska: Estymatory odporne zmienności w modelu Blacka-Scholesa. [dostęp 2008-05-23]. [zarchiwizowane z tego adresu (2007-07-08)].
- Olfa Nasraoui: A Brief Overview of Robust Statistics. [dostęp 2008-05-23]. [zarchiwizowane z tego adresu (2008-04-30)]. (ang.).
- B.D. Ripley: Robust Statistics. [dostęp 2008-05-23]. [zarchiwizowane z tego adresu (2012-10-21)]. (ang.).