Funkcja błędu

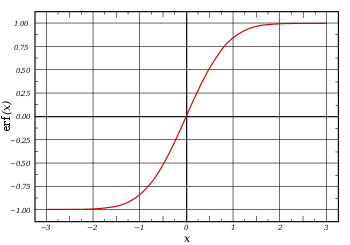
Funkcja błędu (funkcja błędu Gaussa) - funkcja nieelementarna oznaczana symbolem $\operatorname {erf}$ , zdefiniowana za pomocą całki

\operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,\mathrm {d} t.

Funkcja błędu występuje w rachunku prawdopodobieństwa, statystyce oraz w teorii równań różniczkowych cząstkowych.

Zespolona funkcja błędu

Definiuje się zespoloną funkcję błędu $w(x),$ nazywaną także funkcją Faddiejewej:

w(x)=e^{-x^{2}}[1-\operatorname {erf} (-ix)]

Najważniejsze własności i zastosowania

Tw. 1 Funkcja błędu jest nieparzysta, tj.

\operatorname {erf} (-z)=-\operatorname {erf} (z).

Tw. 2 Prawdziwa jest zależność

\operatorname {erf} (z^{*})=[\operatorname {erf} (z)]^{*},

gdzie $z^{*}$ oznacza sprzężenie zespolone liczby $z.$

Czyli: Wartość funkcji błędu obliczonej dla sprzężenia zespolonego $z^{*}$ liczby $z$ jest równa sprzężeniu zespolonemu wartości tej funkcji obliczonej dla liczby $z$ .

Tw. 3 (wartości w nieskończonościach)

a). W nieskończonościach na osi rzeczywistej mamy wartości graniczne

\operatorname {erf} (\pm \infty )=\pm 1

b). W nieskończonościach na osi urojonej mamy

\operatorname {erf} (\pm i\infty )=\pm i\infty

Tw. 4 Funkcja błędu jest ściśle związana z rozkładem normalnym Gaussa. Można to zauważyć, wyliczając pochodną i funkcję pierwotną funkcji błędu:

{\frac {d}{dz}}\operatorname {erf} (z)={\frac {2}{\sqrt {\pi }}}e^{-z^{2}},

F(z)=z\,\operatorname {erf} (z)+{\frac {e^{-z^{2}}}{\sqrt {\pi }}}.

Rozwinięcia w szeregi potęgowe

(1) Przez zapisanie prawej strony definicji jako szereg Taylora i całkowanie, można dowieść, że

{\begin{aligned}\operatorname {erf} (x)&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)n!}}\\&={\frac {2}{\sqrt {\pi }}}\left(x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{10}}-{\frac {x^{7}}{42}}+{\frac {x^{9}}{216}}-\ \ldots \right)\end{aligned}}

dla każdego rzeczywistego $x.$

(2) Dla $|x|\ll 1$ wartość funkcji błędu można wyliczyć z dużą dokładnością z rozwinięcia (ograniczając się do początkowych kilkunastu wyrazów)

{\begin{aligned}\operatorname {erf} (x)&={\frac {2}{\sqrt {\pi }}}e^{-x^{2}}\sum _{n=0}^{\infty }{\frac {2^{n}}{(2n+1)!!}}x^{2n+1}\\&={\frac {2}{\sqrt {\pi }}}e^{-x^{2}}\left(x+{\frac {2x^{3}}{1\cdot 3}}+{\frac {4x^{5}}{1\cdot 3\cdot 5}}+{\frac {8x^{7}}{1\cdot 3\cdot 5\cdot 7}}+\ldots \right),\end{aligned}}

gdzie $k!!$ oznacza silnię podwójną liczby $k.$

(3) Dla $|x|\gg 1$ wartość funkcji błędu można wyliczyć z dużą dokładnością z rozwinięcia ${\begin{aligned}\operatorname {erf} (x)&=1-{\frac {e^{-x^{2}}}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n-1)!!}{2^{n}}}x^{-2n-1}\\&=1-{\frac {e^{-x^{2}}}{\sqrt {\pi }}}\left({\frac {1}{x}}-{\frac {1}{2x^{3}}}+{\frac {1\cdot 3}{4x^{5}}}-{\frac {1\cdot 3\cdot 5}{8x^{7}}}+\ldots \right).\end{aligned}}$

ograniczając się do początkowych kilkunastu wyrazów

Przybliżenia za pomocą funkcji elementarnych

(1) Funkcje błędu można dobrze przybliżyć przez podobnie wyglądające funkcje cyklometryczne i funkcje hiperboliczne typu tangens, tzn. $\operatorname {arctg} (x)$ i $\operatorname {tgh} (x){:}$

\operatorname {erf} (x)\approx {\frac {2}{\pi }}\operatorname {arctg} [2x(1+x^{4})]

oraz

\operatorname {erf} (x)\approx \operatorname {sgn}(x)\operatorname {tgh} [1{,}152|x|+0{,}064|x|^{4}].

Są one więc także odwracalne poprzez rozwiązanie zredukowanego równania czwartego i piątego stopnia.

(2) Także bardzo dokładne i odwracalne przybliżenie funkcji błędu (błąd poniżej 0,00035) można uzyskać poprzez deformacje odjęcia funkcji Gaussa od jedynki:

\operatorname {erf} (x)\approx \operatorname {sgn}(x){\sqrt {1-e^{-\alpha (x)x^{2}}}},

gdzie:

\alpha (x)={\frac {{\frac {4}{\pi }}+ax^{2}}{1+ax^{2}}}

jest przybliżeniem Padégo rzędu $(2,2)$ zmieniającej się szerokości funkcji Gaussa; $a={\tfrac {8(\pi -3)}{3\pi (4-\pi )}}\approx 0{,}140012$ .

(3) Przybliżenie to można jeszcze poprawić, redukując błąd do $1{,}5\times 10^{-5}$

\operatorname {erf} (x)\approx \operatorname {sgn}(x)\left[{\sqrt {1-e^{-\alpha (x)x^{2}}}}-0{,}0026P(7{,}13|x|+0{,}0001,\lambda )\right],

gdzie $P(x)$ $(x>0)$ jest uciąglonym przy pomocy wzoru Stirlinga rozkładem Poissona dla $\lambda =10{,}2$

P(x,\lambda )=e^{-{\lambda }}\lambda ^{x}{\frac {1}{\sqrt {2\pi x}}}\left({\frac {e}{x}}\right)^{x}.

Uzupełniająca funkcja błędu erfc

Z funkcją błędu związana jest uzupełniająca funkcj błędu $\operatorname {erfc} {:}$

{\begin{aligned}\operatorname {erfc} (x)&\equiv 1-\operatorname {erf} (x)\\&={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t.\end{aligned}}

Tablica wartości

x	erf(x)	erfc(x)	x	erf(x)	erfc(x)
0,00	0,0000000	1,0000000	1,30	0,9340079	0,0659921
0,05	0,0563720	0,9436280	1,40	0,9522851	0,0477149
0,10	0,1124629	0,8875371	1,50	0,9661051	0,0338949
0,15	0,1679960	0,8320040	1,60	0,9763484	0,0236516
0,20	0,2227026	0,7772974	1,70	0,9837905	0,0162095
0,25	0,2763264	0,7236736	1,80	0,9890905	0,0109095
0,30	0,3286268	0,6713732	1,90	0,9927904	0,0072096
0,35	0,3793821	0,6206179	2,00	0,9953223	0,0046777
0,40	0,4283924	0,5716076	2,10	0,9970205	0,0029795
0,45	0,4754817	0,5245183	2,20	0,9981372	0,0018628
0,50	0,5204999	0,4795001	2,30	0,9988568	0,0011432
0,55	0,5633234	0,4366766	2,40	0,9993115	0,0006885
0,60	0,6038561	0,3961439	2,50	0,9995930	0,0004070
0,65	0,6420293	0,3579707	2,60	0,9997640	0,0002360
0,70	0,6778012	0,3221988	2,70	0,9998657	0,0001343
0,75	0,7111556	0,2888444	2,80	0,9999250	0,0000750
0,80	0,7421010	0,2578990	2,90	0,9999589	0,0000411
0,85	0,7706681	0,2293319	3,00	0,9999779	0,0000221
0,90	0,7969082	0,2030918	3,10	0,9999884	0,0000116
0,95	0,8208908	0,1791092	3,20	0,9999940	0,0000060
1,00	0,8427008	0,1572992	3,30	0,9999969	0,0000031
1,10	0,8802051	0,1197949	3,40	0,9999985	0,0000015
1,20	0,9103140	0,0896860	3,50	0,9999993	0,0000007

Zobacz też

rozkład normalny

Linki zewnętrzne

Eric W.E.W. Weisstein Eric W.E.W., Erf, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2023-05-31].
Probability integral (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-05-31].

[1] unkcji elementarnych

[a]