Szablon:Rozkład prawdopodobieństwa infobox

{{{nazwa}}}

{{Rozkład prawdopodobieństwa infobox/typ {{{typ}}}}} [[Plik:{{{wykres}}}|250x250px| class=mw-no-invert| alt=Ilustracja|{{{opis wykresu}}}]] {{{opis wykresu}}}
Dystrybuanta [[Plik:{{{wykres_dystrybuanty}}}|250x250px| class=mw-no-invert| alt=Ilustracja|{{{opis wykresu dystrybuanty}}}]] {{{opis wykresu dystrybuanty}}}
Parametry	{{{parametry}}}
Nośnik	{{{nośnik}}}
{{Rozkład prawdopodobieństwa infobox/typ {{{typ}}}}}	{{{prawdopodobieństwo}}}
Dystrybuanta	{{{dystrybuanta}}}
Wartość oczekiwana (średnia)	{{{wartość_oczekiwana}}}
Mediana	{{{mediana}}}
Moda	{{{moda}}}
Wariancja	{{{wariancja}}}
Współczynnik skośności	{{{skośność}}}
Kurtoza nadwyżkowa (eksces)	{{{kurtoza}}}
Entropia	{{{entropia}}}
Funkcja tworząca momenty	{{{momenty}}}
Funkcja charakterystyczna	{{{char}}}
Odkrywca	{{{odkrywca}}}

 Dokumentacja szablonu[zobacz] [edytuj] [historia] • [odśwież] • § podstrony

Użycie

• Przed wstawieniem szablonu zapoznaj się z informacją o roli infoboksu w artykule.

{{Rozkład prawdopodobieństwa infobox
 |nazwa = 
 |typ = 
 |wykres = 
 |opis wykresu =
 |wykres_dystrybuanty = 
 |opis wykresu dystrybuanty =
 |parametry = 
 |nośnik = 
 |prawdopodobieństwo = 
 |dystrybuanta = 
 |wartość_oczekiwana = 
 |mediana = 
 |moda = 
 |wariancja = 
 |skośność = 
 |kurtoza = 
 |entropia = 
 |momenty = 
 |char = 
 |odkrywca = 
}}

Opis parametrów

typ

ciągły / dyskretny

wykres

wykres gęstości lub masy prawdopodobieństwa

nośnik, prawdopodobieństwo, dystrybuanta, wartość_oczekiwana, mediana, moda, wariacja, skośność, kurtoza, entropia, momenty, char

stosujemy znacznik math (Pomoc:Wzory)

prawdopodobieństwo

wzór funkcji masy lub gęstości prawdopodobieństwa

momenty

wzór funkcji tworzącej momenty

char

wzór funkcji charakterystycznej

odkrywca

Imię Nazwisko (data)

Przykład

Rozkład Pareta

Gęstość prawdopodobieństwa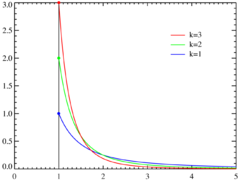 Gęstość prawdopodobieństwa rozkładu Pareta dla różnych k oraz xm = 1. Oś odciętych odpowiada parametrowi x. Dla k dążącego do nieskończoności rozkład zbiega do δ(x − xm) gdzie δ to delta Diraca.
Dystrybuanta Dystrybuanta rozkładu Pareta dla różnych k  oraz xm = 1. Oś odciętych odpowiada parametrowi x.
Parametry	$x_{\mathrm {m} }>0$ parametr skali (liczba rzeczywista) $k>0$ parametr kształtu (liczba rzeczywista)
Nośnik	$x\in [x_{\mathrm {m} };+\infty )$
Gęstość prawdopodobieństwa	${\frac {k\,x_{\mathrm {m} }^{k}}{x^{k+1}}}$
Dystrybuanta	$1-\left({\frac {x_{\mathrm {m} }}{x}}\right)^{k}$
Wartość oczekiwana (średnia)	${\frac {k\,x_{\mathrm {m} }}{k-1}}$ dla $k>1$
Mediana	$x_{\mathrm {m} }{\sqrt[{k}]{2}}$
Moda	$x_{\mathrm {m} }$
Wariancja	${\frac {x_{\mathrm {m} }^{2}k}{(k-1)^{2}(k-2)}}$ dla $k>2$
Współczynnik skośności	${\frac {2(1+k)}{k-3}}\,{\sqrt {\frac {k-2}{k}}}$ dla $k>3$
Kurtoza nadwyżkowa (eksces)	${\frac {6(k^{3}+k^{2}-6k-2)}{k(k-3)(k-4)}}$ dla $k>4$
Entropia	$\ln \left({\frac {k}{x_{\mathrm {m} }}}\right)-{\frac {1}{k}}-1$
Funkcja tworząca momenty	nieokreślona
Funkcja charakterystyczna	$k(-ix_{\mathrm {m} }t)^{k}\Gamma (-k,-ix_{\mathrm {m} }t)$
Odkrywca	Vilfredo Pareto

{{Rozkład prawdopodobieństwa infobox
 |nazwa               = Rozkład Pareta
 |typ                 = ciągły
 |wykres              = Pareto distributionPDF.png
 |opis wykresu        = Gęstość prawdopodobieństwa rozkładu Pareta dla różnych ''k''  oraz ''x''<sub>m</sub> = 1. Oś odciętych odpowiada parametrowi ''x''. Dla ''k'' dążącego do nieskończoności rozkład zbiega do δ(''x'' − ''x''<sub>m</sub>) gdzie δ to [[delta Diraca]].
 |wykres_dystrybuanty = Pareto distributionCDF.png
 |opis wykresu dystrybuanty = Dystrybuanta rozkładu Pareta dla różnych ''k''  oraz ''x''<sub>m</sub> = 1. Oś odciętych odpowiada parametrowi ''x''.
 |parametry           = <math>x_\mathrm{m}>0</math> [[parametr skali]] ([[Liczby rzeczywiste|liczba rzeczywista]])<br /><math>k>0</math> [[parametr kształtu]] (liczba rzeczywista)
 |nośnik              = <math>x \in [x_\mathrm{m}; +\infty)</math>
 |prawdopodobieństwo  = <math>\frac{k\,x_\mathrm{m}^k}{x^{k+1}}</math>
 |dystrybuanta        = <math>1-\left(\frac{x_\mathrm{m}}{x}\right)^k</math>
 |wartość_oczekiwana  = <math>\frac{k\,x_\mathrm{m}}{k-1}</math> dla <math>k>1</math>
 |mediana             = <math>x_\mathrm{m} \sqrt[k]{2}</math>
 |moda                = <math>x_\mathrm{m}</math>
 |wariancja           = <math>\frac{x_\mathrm{m}^2k}{(k-1)^2(k-2)}</math> dla <math>k>2</math>
 |skośność            = <math>\frac{2(1+k)}{k-3}\,\sqrt{\frac{k-2}{k}}</math> dla <math>k>3</math>
 |kurtoza             = <math>\frac{6(k^3+k^2-6k-2)}{k(k-3)(k-4)}</math><br />dla <math>k>4</math>
 |entropia            = <math>\ln\left(\frac{k}{x_\mathrm{m}}\right) - \frac{1}{k} - 1</math>
 |momenty             = nieokreślona
 |char                = <math>k(-ix_\mathrm{m}t)^k\Gamma(-k,-ix_\mathrm{m}t)</math>
 |odkrywca            = [[Vilfredo Pareto]]
}}

Błędy

Błędy należy zgłaszać na stronie Wikipedia:Kawiarenka/Kwestie techniczne.

Parametry szablonu (strukturyzacja VE)

Rozkład prawdopodobieństwa infobox

Parametry szablonu[Zarządzaj dokumentacją szablonu]

Ten szablon ma niestandardowe formatowanie.

Parametr		Opis	Typ	Status
Nazwa	nazwa	brak opisu	Ciąg znaków	wymagany
Typ	typ	Ciągły / dyskretny	Ciąg znaków	wymagany
Wykres	wykres	Wykres gęstości lub masy prawdopodobieństwa	Treść	wymagany
Wykres dystrybuanty	wykres_dystrybuanty	brak opisu	Treść	wymagany
Parametry	parametry	brak opisu	Treść	wymagany
Nośnik	nośnik	brak opisu	Ciąg znaków	wymagany
Opis wykresu	opis wykresu	brak opisu	Treść	wymagany
Opis wykresu dystrybuanty	opis wykresu dystrybuanty	brak opisu	Ciąg znaków	wymagany
Prawdopodobieństwo	prawdopodobieństwo	Wzór funkcji masy lub gęstości prawdopodobieństwa	Ciąg znaków	wymagany
Dystrybuanta	dystrybuanta	brak opisu	Treść	wymagany
Wartość oczekiwana	wartość_oczekiwana	brak opisu	Ciąg znaków	wymagany
Mediana	mediana	brak opisu	Ciąg znaków	wymagany
Moda	moda	brak opisu	Treść	wymagany
Wariancja	wariancja	brak opisu	Ciąg znaków	wymagany
Skośność	skośność	brak opisu	Ciąg znaków	wymagany
Kurtoza	kurtoza	brak opisu	Ciąg znaków	wymagany
Entropia	entropia	brak opisu	Treść	wymagany
Momenty	momenty	Wzór funkcji tworzącej momenty	Ciąg znaków	wymagany
Char	char	Wzór funkcji charakterystycznej	Ciąg znaków	wymagany
Odkrywca	odkrywca	Imię Nazwisko (data)	Treść	wymagany

Powyższy opis jest dołączany ze strony Szablon:Rozkład prawdopodobieństwa infobox/opis. (edytuj | historia)

Zobacz wszystkie podstrony tej strony.

Kategorie należy dodawać do podstrony /opis.