Przenikalność magnetyczna
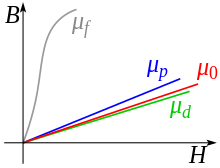
Przenikalność magnetyczna – wielkość określająca zdolność danego materiału (ośrodka) do zmiany indukcji magnetycznej przy zmianie natężenia pola magnetycznego[1].
W próżni[edytuj | edytuj kod]
Przenikalność magnetyczna próżni, zgodnie z danymi opublikowanymi w 2002 roku przez Komitet Danych dla Nauki i Techniki (CODATA), jest skalarem, który oznacza się symbolem μ0 i którego wartość wynosi w układzie SI:
Dla próżni doskonałej spełnione jest więc równanie:
W paramagnetykach i diamagnetykach[edytuj | edytuj kod]
W próżni doskonałej brak jest jakichkolwiek atomów lub cząsteczek, które mogłyby wpłynąć na zależność Wobec tego w każdym ośrodku materialnym powyższe równanie będzie zmodyfikowane w związku z pojawieniem się przenikalności magnetycznej tego ośrodka. Jeśli ośrodkiem jest paramagnetyk lub diamagnetyk przenikalność magnetyczna jest również skalarem i można zapisać:
gdzie:
- – względna przenikalność magnetyczna ośrodka (liczba bezwymiarowa) określana jako stosunek przenikalności magnetycznej (bezwzględnej μ) danego ośrodka do przenikalności magnetycznej próżni.
Dla próżni przenikalność względna jest równa dokładnie 1. Dla paramagnetyków przenikalność względna jest niewiele większa od 1, dla diamagnetyków jest niewiele mniejsza od jedności – dla obydwu tych typów ośrodków różnica jest na tyle niewielka, że w zastosowaniach technicznych często się ją zaniedbuje przyjmując wartość równą 1.
W ferromagnetykach[edytuj | edytuj kod]

W przypadku ferromagnetyków przenikalność względna nie może zostać opisana jedną liczbą (skalarem). Dla jednoosiowego przemagnesowania przenikalność względna ferromagnetyków określana jest nieliniową funkcją:
Podczas projektowania obwodów magnetycznych stosuje się uproszczenie polegające na tym, że przenikalność ma jedną wartość w danym punkcie pracy urządzenia. W takim przypadku konkretną wartość przenikalności oblicza się jako:
gdzie:
- – szczytowa wartość przebiegu indukcji magnetycznej,
- – szczytowa wartość przebiegu natężenia pola magnetycznego.
Funkcja ta ma pewną początkową wartość, zazwyczaj dużo większą od 1, zwaną przenikalnością początkową, następnie osiąga maksimum, po czym dla bardzo wysokich wartości pola magnetycznego, w miarę zbliżania się do nasycenia magnetycznego, wartość ta zbliża się do jedności (przenikalność względna materiału zbliża się do wartości przenikalności próżni).
Jest to bardzo uproszczone podejście stosowane w ogólnie elektrotechnice i praktyce projektowania obwodów magnetycznych, gdzie niezbędne jest określenie wartości reluktancji. W ścisłym, fizycznym opisie przenikalność może przyjąć nawet postać tensora.
Tabela przenikalności magnetycznej względnej[2][3][edytuj | edytuj kod]
| Materiał | Przenikalność początkowa | Przenikalność maksymalna |
|---|---|---|
| Próżnia | 1 | 1 |
| Powietrze | 1,00000037 | (brak informacji) |
| Aluminium | 1,000020 | (brak informacji) |
| Miedź | 0,99999 | (brak informacji) |
| Izotropowa blacha elektrotechniczna (Fe96Si4) | 250 | 7 000 |
| Anizotropowa blacha elektrotechniczna (Fe97Si3) | (brak informacji) | 100 000 |
| Permendur (Co50Fe50) | (brak informacji) | 5 000 |
| Supermaloj (Ni79Fe15Mo5) | (brak informacji) | 1 000 000 |
| Monokrystaliczny stop (Fe97Si3) | (brak informacji) | 3 800 000 |
| Blacha transformatorowa | 600 | 7 600 |
| Żelazo elektrolityczne | 600 | 15 000 |
| Stop nikiel-żelazo | 2 700 | 20 000 |
| Bizmut | 0,999824 | (brak informacji) |
| Szkło | 0,999987 | (brak informacji) |
| Woda | 0,999991 | (brak informacji) |
| Wodór | 0,999999937 | (brak informacji) |
| Tlen | 1,0000019 | (brak informacji) |
| Wolfram | 1,000176 | (brak informacji) |
Warto zwrócić uwagę, że przenikalność ciał ferromagnetycznych zależy w dużym stopniu od rodzaju stopu i od sposobu obróbki. Wartość przenikalności wzrasta do pewnej granicy wraz z natężeniem pola.
Czynniki wpływające na przenikalność w ferromagnetykach[edytuj | edytuj kod]
Wartości przenikalności względnej w ferromagnetykach zależą nie tylko od składu chemicznego materiału, ale również od bardzo wielu innych czynników. Na przykład przenikalność względna nieznacznie rośnie ze wzrostem rozciągających naprężeń mechanicznych wywołanych wzdłuż kierunku magnesowania, ale silnie maleje dla naprężeń ściskających, ponieważ prowadzi to do zmian w strukturze domenowej.
Bardzo ważnym czynnikiem jest więc odpowiednia obróbka mechaniczna materiału, jak również obróbka termiczna, za pomocą której można usuwać niepożądane wewnętrzne naprężenia mechaniczne powstałe podczas produkcji materiału. Z drugiej strony, wprowadzając odpowiednio ukształtowane naprężenia mechaniczne można znacznie zwiększyć przenikalność. Metoda taka jest stosowana np. w wysokiej jakości anizotropowych blachach elektrotechnicznych (używanych np. do produkcji transformatorów), gdzie użycie odpowiedniej powłoki izolującej połączonej z wprowadzeniem precyzyjnie umieszczonych lokalnych naprężeń mechanicznych (za pomocą naświetlania promieniem lasera lub rolując powierzchnię materiału przy pomocy bardzo utwardzonych kul stalowych) następuje polepszenie magnetycznej struktury domenowej skutkującej obniżeniem strat mocy i zwiększeniem przenikalności.
Bardzo ważnym czynnikiem jest również temperatura pracy materiału – im bliżej jest ona temperatury Curie tym szybciej maleje przenikalność ferromagnetyka.
Zastosowanie praktyczne[edytuj | edytuj kod]
Najczęściej wykorzystywane są dwa aspekty względnej przenikalności magnetycznej:
- Liniowość przenikalności dla paramagnetyków i diamagnetyków
- wykorzystuje się między innymi w różnych indukcyjnych czujnikach magnetycznych (np. cewka Rogowskiego), dla których można łatwo wyliczyć zależność pomiędzy przenikającym polem magnetycznym i napięciem indukowanym na cewce czujnika. Przemienne lokalne pole magnetyczne można zmierzyć za pomocą zwykłej cewki nawiniętej na dowolnym niemagnetycznym rdzeniu, przy znajomości parametrów cewki, lub jej uprzednim skalibrowaniu. Nie ma praktycznego znaczenia czy rdzeń jest paramagnetyczny czy diamagnetyczny – obie wartości przenikalności są bardzo bliskie jedności i popełniany błąd jest zaniedbywalny. Dodatkową zaletą jest również to, że dla bardzo wysokich wartości pola magnetycznego funkcja przenikalności pozostaje stała (brak nasycenia magnetycznego), co umożliwia uzyskanie bardzo dużych indukcji (nawet rzędu 100 T). W teorii tak dużą indukcję można również uzyskać dla ferromagnetyków, jednak przy przemagnesowaniu przemiennym straty mocy byłyby bardzo duże, za to przemagnesowanie dia- i paramagnetyków jest bezstratne (jeśli nie są one przewodnikami).
- Duża wartość przenikalności dla ferromagnetyków
- wykorzystywana jest w różnego typu urządzeniach odpowiedzialnych za transformację energii pomiędzy różnymi poziomami tej samej energii (transformator) lub zamianę z jednego rodzaju energii na inny (prądnica, silnik elektryczny). Pomimo tego, że w ferromagnetycznym rdzeniu występują pewne straty mocy, to jednak skupienie energii w rdzeniu ferromagnetycznym jest o wiele bardziej korzystne i umożliwia uzyskanie tego same efektu przy znacznie mniejszych prądach magnesujących (czyli mniejszych stratach mocy w uzwojeniach elektrycznych takiego obwodu). Praktycznie często zakłada się, że wartość przenikalności magnetycznej jest stała dla ferromagnetyków do wartości magnetyzacji nasycenia, lub w danym punkcie pracy. Przenikalność względna ferromagnetyków jest co najmniej kilka tysięcy razy większa niż innych materiałów – oznacza to, że o tyle razy łatwiej jest uzyskać taką samą gęstość energii magnetycznej w ferromagnetyku, niż w innym materiale.
Rodzaje przenikalności[edytuj | edytuj kod]
Dla ośrodków nieliniowych jakimi są ferromagnetyki przenikalność magnetyczna danego ośrodka nie jest wartością stałą, lecz zależy od wielu czynników dlatego definiuje się szczególne współczynniki określające przenikalność w zadanych warunkach. Wyróżnić można między innymi:
- przenikalność początkową (definiowana dla H dążącego do zera):
- przenikalność maksymalną (opisana powyżej):
- przenikalność powrotną (w punkcie pracy):
- przenikalność rewersyjną:
- przenikalność impulsową.
Zobacz też[edytuj | edytuj kod]
Przypisy[edytuj | edytuj kod]
- ↑ Przenikalność magnetyczna, [w:] Encyklopedia PWN [dostęp 2021-07-23].
- ↑ Tomasz Szymczyk, Tablice matematyczne, fizyczne, chemiczne, astronomiczne, Warszawa: Świat Książki, 2003, ISBN 83-7391-162-6, OCLC 749236015 [dostęp 2022-06-02].
- ↑ Tablice matematyczne, fizyczne, chemiczne i astronomiczne, Warszawa: Wydawnictwa Szkolne i Pedagogiczne, 1984, ISBN 83-02-00763-3.
Bibliografia[edytuj | edytuj kod]
- B. Jaworski, A. Dietłaf, L. Miłkowska, G. Siergiejew, Kurs fizyki. Elektryczność i magnetyzm, t. 2, Państwowe Wydawnictwo Naukowe, Warszawa 1984, wyd.8, ISBN 83-01-01265-X.













