Regresja logistyczna

Regresja logistyczna – jedna z metod regresji używanych w statystyce w przypadku, gdy zmienna objaśniana jest na skali dychotomicznej (przyjmuje tylko dwie wartości).

Zwykle wartości zmiennej objaśnianej wskazują na wystąpienie, lub brak wystąpienia pewnego zdarzenia, które chcemy prognozować. Regresja logistyczna pozwala wówczas na obliczanie prawdopodobieństwa tego zdarzenia (tzw. prawdopodobieństwo sukcesu).

Formalnie model regresji logistycznej jest uogólnionym modelem liniowym (GLM), w którym użyto logitu jako funkcji wiążącej.

Szansa

Regresja logistyczna opiera się na specyficznym sposobie wyrażania prawdopodobieństwa, zwanym szansą (ang. odds).

Zamiast określać prawdopodobieństwo klasycznie, za pomocą stosunku liczby sukcesów do liczby wszystkich prób, oblicza się szansę, czyli stosunek liczby sukcesów do liczby porażek.

Można ją łatwo wyliczyć ze zwykłego prawdopodobieństwa:

$Odds=\frac{p}{1-p}$

Istnieje też odwrotne przekształcenie:

$p=\frac{Odds}{1+Odds}$

Szansa ma pewną zaletę w porównaniu ze zwykłym zapisem prawdopodobieństwa — przyjmuje dla $0<p<1$ wartości z zakresu $(0,+\infty)$ a jej logarytm wartości z zakresu $(-\infty,\infty)$.

Dzięki temu można stosować do szacowania logarytmu szansy metody regresji nie ograniczone do przedziału [0,1] (np. regresję liniową).

Funkcja logit

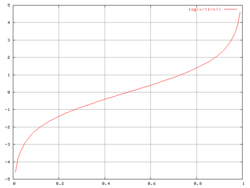
Funkcja przekształcająca prawdopodobieństwo na logarytm szansy zwana jest logitem:

$\operatorname{logit}(p)=\operatorname{ln} \frac{p}{1-p}=\operatorname{ln}(p)-\operatorname{ln}(1-p)$

Funkcja odwrotna:

$p=\frac{e^{\operatorname{logit}(p)}}{1+e^{\operatorname{logit}(p)}}=\frac{1}{1+e^{-\operatorname{logit}(p)}}$

Model regresji logistycznej

Regresja logistyczna zakłada, że zmienna objaśniana ma rozkład dwupunktowy:

$Y_i \ \sim B(p_i,n_i),$ dla $i=1,\dots ,m$

gdzie liczba prób w procesie Bernoulliego $n_i$ jest znana, a prawdopodobieństwo sukcesu $p_i$ jest nieznane. Przykładem tej sytuacji jest rozkład odsetka kwiatów, które zakwitną, wśród $n_i$ sadzonek.

Model zakłada, że dla każdej próby Bernoulliego (wartość $i$), istnieje zbiór $k$ zmiennych objaśniających, które niosą pewną informację na temat prawdopodobieństwa sukcesu. Te zmienne objaśniające można uważać za $k$-elementowy wektor losowy $X_i$. Model przyjmuje wówczas postać:

$p_i = \operatorname{E}\left(\left.\frac{Y_i}{n_{i}}\right|X_i \right). \,\!$

Logit nieznanego prawdopodobieństwa sukcesu $p_i$ jest modelowany jako liniowa funkcja $X_i$:

$\operatorname{logit}(p_i)=\ln\left(\frac{p_i}{1-p_i}\right) = \beta_1 x_{1,i} + \cdots + \beta_k x_{k,i}.$

Do modelu można wprowadzić stałą, tworząc zmienną objaśniającą, mającą wszędzie wartość 1, czyli ustawiając $x_{j,i}=1$ dla pewnego $j$ i wszystkich $i$. Nieznane parametry $\beta_j$ są zwykle estymowane metodą największej wiarygodności.

Interpretacją estymowanego parametru $\beta_j$ jest addytywny wpływ, jaki ma jednostkowa zmiana zmiennej $j$ na logarytm odds ratio

W przypadku zmiennych objaśniających na skali dychotomicznej (np. płeć), $e^\beta$ jest estymacją szansy, powiedzmy, mężczyzn w porównaniu z kobietami.

Model posiada równoważne sformułowanie w postaci:

$p_i = \frac{1}{1+e^{-(\beta_1 x_{1,i} + \cdots + \beta_k x_{k,i})}}. \,\!$

Ta forma funkcjonalna jest znana jako perceptron lub jednowarstwowa sieć neuronowa.

Rozszerzenia

Istnieją rozszerzenia modelu, pozwalające na użycie także zmiennych objaśniających na skali nominalnej oraz porządkowej.

Inne rozszerzenie pozwala na zmienną objaśnianą przyjmującą więcej niż dwie wartości (tzw. multinomial logit)

Odmianą jest regresja probitowa, w której zamiast funkcji logit stosuje się odwrotną dystrybuantę rozkładu normalnego (tzw. probit)

Zobacz też

• sieć neuronowa
• eksploracja danych
• liniowa analiza dyskryminacyjna
• perceptron
• probit

Linki zewnętrzne

• Internetowy kalkulator regresji logistycznej (ang.)
• Pakiet Javy o nazwie Mallet, zawiera moduł regresji logistycznej (ang.)

Bibliografia

• Alan. Agresti: Categorical Data Analysis. Wiley-Interscience, Nowy Jork, 2002. ISBN 0-471-36093-7.
• T. Amemiya: Advanced Econometrics. Harvard University Press, 1985. ISBN 0-674-00560-0.
• N. Balakrishnan: Handbook of the Logistic Distribution. Marcel Dekker, Inc., 1991. ISBN 978-0-8247-8587-1.
• William H. Green: Econometric Analysis, fifth edition. Prentice Hall, 2003. ISBN 0-13-066189-9.
• David W. Hosmer: Applied Logistic Regression, 2nd ed.. Chichester, Wiley, Nowy Jork, 2000. ISBN 0-471-35632-8.