Szereg Fouriera

Szereg Fouriera – szereg pozwalający rozłożyć funkcję okresową, spełniającą warunki Dirichleta, na sumę funkcji trygonometrycznych. Nauka na temat szeregów Fouriera jest gałęzią analizy Fouriera. Szeregi Fouriera zostały wprowadzone w 1807 roku przez Josepha Fouriera w celu rozwiązania równania ciepła dla metalowej płyty. Doprowadziło to jednak do przewrotu w matematyce i wprowadzenia wielu nowych teorii. Dziś mają one wielkie znaczenie między innymi w fizyce, teorii drgań oraz przetwarzaniu sygnałów obrazu (kompresja jpeg) i dźwięku (kompresja mp3).

Definicja

Niech dana będzie funkcja okresowa $f\colon \mathbb {R} \to \mathbb {R}$ o okresie $T\in \mathbb {R} ^{+},$ bezwzględnie całkowalna w przedziale $\left[{\frac {-T}{2}},{\frac {T}{2}}\right].$

Trygonometrycznym szeregiem Fouriera funkcji $f$ nazywamy szereg funkcyjny następującej postaci:

$S(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left(a_{n}\cos \left({\frac {2n\pi }{T}}x\right)+b_{n}\sin \left({\frac {2n\pi }{T}}x\right)\right)$

(1.1)

o współczynnikach określonych następującymi wzorami:

$a_{n}={\frac {2}{T}}\int \limits _{-{\frac {T}{2}}}^{\frac {T}{2}}f(x)\cos \left({\frac {2n\pi }{T}}x\right)dx,\quad n=0,1,2,\dots ,$

(1.2)

$b_{n}={\frac {2}{T}}\int \limits _{-{\frac {T}{2}}}^{\frac {T}{2}}f(x)\sin \left({\frac {2n\pi }{T}}x\right)dx,\quad n=1,2,3,\dots$

(1.3)

Powyższe wzory po raz pierwszy ujrzały światło dzienne w pracach Jeana-Baptiste Josepha Fouriera. Niemniej jednak po raz pierwszy wyprowadził je Leonhard Euler (prac na ten temat nie opublikował). Z tego względu wzory te noszą nazwę wzorów Eulera-Fouriera.

W fizyce i technice często spotykane jest następujące oznaczenie ($T$ oznacza okres funkcji) $\omega ={\frac {2\pi }{T}}.\ {}$ $\omega$ nosi nazwę pulsacji lub częstości kołowej. Przy zastosowaniu takiego oznaczenia powyższe wzory przyjmują postać:

$S(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left(a_{n}\cos \left(n\omega x\right)+b_{n}\sin \left(n\omega x\right)\right),$

(1.1a)

$a_{n}={\frac {2}{T}}\int \limits _{-{\frac {T}{2}}}^{\frac {T}{2}}f(x)\cos \left(n\omega x\right)dx,\quad n=0,1,2,\dots ,$

(1.2a)

$b_{n}={\frac {2}{T}}\int \limits _{-{\frac {T}{2}}}^{\frac {T}{2}}f(x)\sin \left(n\omega x\right)dx,\quad n=1,2,3,\dots$

(1.3a)

Własności

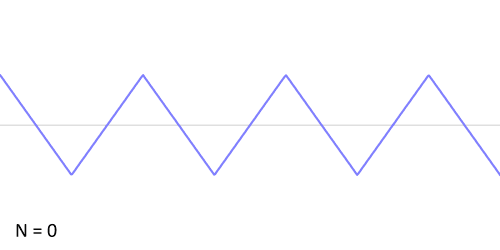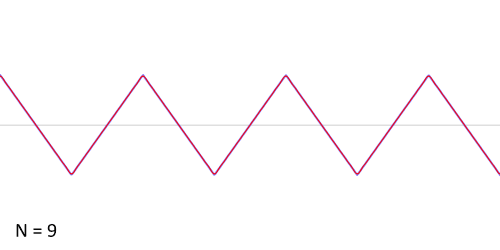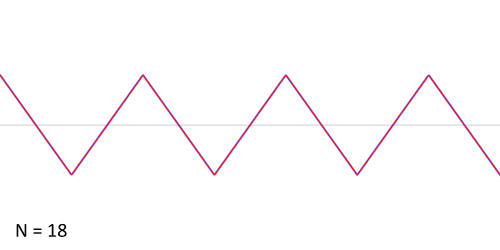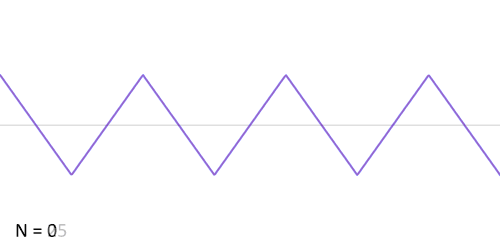
Aproksymacja fali prostokątnej szeregiem Fouriera

Aproksymacja fali piłokształtnej szeregiem Fouriera

Aproksymacja fali trójkątnej szeregiem Fouriera

Poniższe twierdzenia dot. rozwijalności funkcji w szereg Fouriera. W dalszym ciągu zakładamy, że okres funkcji wynosi 2T.

Lemat I (całki pomocnicze)

• $n$ jest liczbą całkowitą

$\int \limits _{-T}^{T}\cos n\omega xdx=\left\{{\begin{aligned}&0&&{\text{gdy}}~~n\neq 0\\&2T&&{\text{gdy}}~~n=0\end{aligned}}\right.,$

$\int \limits _{-T}^{T}\sin n\omega xdx=0.$

• $m,\ n$ są liczbami naturalnymi

$\int \limits _{-T}^{T}\cos n\omega x\cos m\omega xdx=\left\{{\begin{aligned}&0&&{\text{gdy}}~~n\neq m\\&T&&{\text{gdy}}~~n=m\end{aligned}}\right.,$

$\int \limits _{-T}^{T}\sin n\omega x\sin m\omega xdx=\left\{{\begin{aligned}&0&&{\text{gdy}}~~n\neq m\\&T&&{\text{gdy}}~~n=m\end{aligned}}\right.,$

$\int \limits _{-T}^{T}\sin n\omega x\cos m\omega xdx=0.$

Lemat II

${\frac {1}{2}}+\sum _{n=1}^{N}\cos n\alpha ={\frac {\sin \left(N+{\frac {1}{2}}\right)\alpha }{2\sin {\frac {1}{2}}\alpha }}$

Dowód

${\begin{aligned}&\;{\frac {1}{2}}+\sum _{n=1}^{N}\cos n\alpha \\=&\ \Re \left(-{\frac {1}{2}}+\sum _{n=0}^{N}e^{in\alpha }\right)\\=&\ \Re \left(-{\frac {1}{2}}+{\frac {1-e^{i(N+1)\alpha }}{1-e^{i\alpha }}}\right)\\=&-{\frac {1}{2}}+{\frac {1}{|1-e^{i\alpha }|^{2}}}\Re ((1-e^{i(N+1)\alpha })(1-e^{-i\alpha }))\\=&-{\frac {1}{2}}+{\frac {1}{(1-\cos \alpha )^{2}+\sin ^{2}\alpha }}\Re (1-e^{-i\alpha }-e^{i(N+1)\alpha }+e^{iN\alpha })\end{aligned}}$

więc mamy (biorąc cześć rzeczywistą i stosując podstawowe wzory trygonometryczne):

${\begin{aligned}&{\frac {1}{2}}+\sum _{n=1}^{N}\cos n\alpha \\=&-{\frac {1}{2}}+{\frac {1-\cos \alpha -\cos(N+1)\alpha +\cos N\alpha }{2(1-\cos \alpha )}}\\=&\;{\frac {\cos N\alpha -\cos(N+1)\alpha }{2(1-\cos \alpha )}}\\=&\;{\frac {2\sin \left(N+{\frac {1}{2}}\right)\alpha \sin {\frac {1}{2}}\alpha }{4\sin ^{2}{\frac {1}{2}}\alpha }}\\=&\;{\frac {\sin \left(N+{\frac {1}{2}}\right)\alpha }{2\sin {\frac {1}{2}}\alpha }}\end{aligned}}$

q. e. d.

Lemat III

Jeżeli $f$ jest funkcją ciągłą w przedziale $[a,b]$ z wyjątkiem co najwyżej skończonej ilości punktów i bezwzględnie całkowalną w tym przedziale to

$\lim _{n\to \infty }\int \limits _{a}^{b}f(x)\sin nx\,{\text{d}}x=0.$

Twierdzenie (Eulera–Fouriera)

Jeżeli szereg o postaci (1.1) jest jednostajnie zbieżny do funkcji $f$ to współczynniki $a_{k},\ b_{k}$ wyrażają się wzorami (1.2), (1.3).

Dowód

$f(x)={\frac {a_{0}}{2}}+\sum _{k=1}^{\infty }\left(a_{k}\cos k\omega x+b_{k}\sin k\omega x\right).$

Mnożąc powyższą równość przez $\cos n\omega x,$ całkując szereg w granicach od $-T$ do $T$ (uwzględniając zbieżność jednostajną szeregu stosujemy twierdzenie o całkowaniu szeregu wyraz po wyrazie) otrzymujemy:

$\int \limits _{-T}^{T}f(x)\cos n\omega x{\text{d}}x={\frac {a_{0}}{2}}\int \limits _{-T}^{T}\cos n\omega x{\text{d}}x+\sum _{k=1}^{\infty }\left(a_{k}\int \limits _{-T}^{T}\cos n\omega x\cos k\omega x{\text{d}}x+b_{k}\int \limits _{-T}^{T}\cos n\omega x\sin k\omega x{\text{d}}x\right).$

Na mocy lematu I zerują się wszystkie całki po prawej stronie takie że $n\neq k$ (gdy $n=0$ zeruje się cała suma uogólniona). W związku z tym mamy:

$\int \limits _{-T}^{T}f(x)\cos n\omega x{\text{d}}x=a_{n}T.$

Stąd otrzymujemy wzór (1.2).

Dowód wzoru (1.3) przebiega analogicznie (tym razem mnożymy przez $\sin n\omega x$)

Twierdzenie (o rozwijalności funkcji w szereg Fouriera)

Jeżeli funkcja f(x) jest różniczkowalna w punkcie $x_{0},$ to jej szereg Fouriera jest zbieżny do wartości funkcji w tym punkcie. Innymi słowy: w punktach różniczkowalności funkcję da się rozwinąć w szereg Fouriera.

Dowód

Niech $x_{0}$ będzie punktem, w którym funkcja f(x) jest różniczkowalna; mamy:

${\begin{aligned}&\;a_{n}\cos n\omega x_{0}+b_{n}\sin n\omega x_{0}\\=&\;{\frac {1}{T}}\int \limits _{-T}^{T}f(x)\cos n\omega xdx\cos n\omega x_{0}+{\frac {1}{T}}\int \limits _{-T}^{T}f(x)\sin n\omega xdx\sin n\omega x_{0}\\=&\;{\frac {1}{T}}\int \limits _{-T}^{T}f(x)(\cos n\omega x\cos n\omega x_{0}+\sin n\omega x\sin n\omega x_{0})dx\\=&\;{\frac {1}{T}}\int \limits _{-T}^{T}f(x)\cos n\omega (x-x_{0})dx.\end{aligned}}$

Suma cząstkowa szeregu Fouriera przedstawia się w następujący sposób:

${\begin{aligned}S_{N}&={\frac {1}{2T}}\int \limits _{-T}^{T}f(x)dx+\sum _{n=1}^{N}{\frac {1}{T}}\int \limits _{-T}^{T}f(x)\cos n\omega (x-x_{0})dx\\&={\frac {1}{T}}\int \limits _{-T}^{T}f(x)\left({\frac {1}{2}}+\sum _{n=1}^{N}\cos n\omega (x-x_{0})\right)dx.\end{aligned}}$

Stosując do tego wyrażenia lemat II, otrzymujemy następujący wzór:

$S_{N}={\frac {1}{T}}\int \limits _{-T}^{T}f(x){\frac {\sin \omega \left(N+{\frac {1}{2}}\right)(x-x_{0})}{2\sin \omega {\frac {1}{2}}(x-x_{0})}}dx.$

Funkcja podcałkowa w powyższym wzorze jest funkcją o okresie 2T, możemy więc dokonać przesunięcia w dziedzinie i otrzymujemy:

$S_{N}={\frac {1}{T}}\int \limits _{-T}^{T}f(x+x_{0}){\frac {\sin \omega \left(N+{\frac {1}{2}}\right)x}{2\sin \omega {\frac {1}{2}}x}}dx.$

Funkcja tożsamościowo równa 1 na całym zbiorze liczb rzeczywistych jest rozwijalna w szereg Fouriera w każdym punkcie, kładąc $f(x)=1,$ mamy:

$1={\frac {1}{T}}\int \limits _{-T}^{T}{\frac {\sin \omega \left(N+{\frac {1}{2}}\right)x}{2\sin \omega {\frac {1}{2}}x}}dx.$

Mnożąc powyższą równość przez $f(x_{0})$ i odejmując obustronnie od równania przedstawiającego sumę cząstkową szeregu, otrzymujemy:

$S_{N}-f(x_{0})={\frac {1}{T}}\int \limits _{-T}^{T}(f(x+x_{0})-f(x_{0})){\frac {\sin \omega \left(N+{\frac {1}{2}}\right)x}{2\sin \omega {\frac {1}{2}}x}}dx.$

(2)

Rozważmy następującą granicę:

$\lim _{x\to 0}{\frac {f(x+x_{0})-f(x_{0})}{2\sin \omega {\frac {1}{2}}x}}=\lim _{x\to 0}{\frac {f(x+x_{0})-f(x_{0})}{x}}{\frac {x}{2\sin \omega {\frac {1}{2}}x}}={\frac {f'(x_{0})}{\omega }},$

przy obliczaniu której korzystamy z różniczkowalności funkcji f(x) w punkcie $x_{0}.$

Możemy określić następującą funkcję:

$\phi (x)=\left\{{\begin{aligned}&{\frac {f(x+x_{0})-f(x_{0})}{2\sin \omega {\frac {1}{2}}x}}&&{\text{gdy}}~~x\neq 0\\&{\frac {f'(x_{0})}{\omega }}&&{\text{gdy}}~~x=0\end{aligned}}\right..$

Mając na uwadze fakt, iż zmiana skończonej ilości wartości funkcji podcałkowej nie wpływa na wartość całki, wzór (2) możemy zapisać w postaci:

$S_{N}-f(x_{0})={\frac {1}{T}}\int \limits _{-T}^{T}\phi (x)\sin \omega \left(N+{\frac {1}{2}}\right)xdx.$

Funkcja podcałkowa spełnia założenia lematu Riemanna, tak więc:

$\lim _{N\to \infty }(S_{N}-f(x_{0}))=\lim _{N\to \infty }{\frac {1}{T}}\int \limits _{-T}^{T}\phi (x)\sin \omega \left(N+{\frac {1}{2}}\right)xdx=0,$

czyli:

$\lim _{N\to \infty }S_{N}=f(x_{0}).$

q. e. d.

Linki zewnętrzne

Polskojęzyczne

• Materiały dydaktyczne DSP AGH. dsp.agh.edu.pl. [zarchiwizowane z tego adresu (2013-12-17)].

Anglojęzyczne

• Eric W.E.W. Weisstein Eric W.E.W., Fourier Series, [w:] MathWorld [online], Wolfram Research [dostęp 2020-12-12]  (ang.).
• Aplet Java obrazujący idee szeregu Fouriera
• Grant Sanderson, But what is a Fourier series? From heat flow to circle drawings, kanał 3blue1brown na YouTube, 30 czerwca 2019 [dostęp 2021-03-15].