Przeszukiwanie w głąb
| Przeszukiwanie w głąb | ||||||||
|---|---|---|---|---|---|---|---|---|
 |
||||||||
| Podstawowe informacje | ||||||||
|
h-długość najdłuższej prostej ścieżkiNiniejszy artykuł jest częścią cyklu teoria grafów.
 |
|
Najważniejsze pojęcia Wybrane klasy grafów Algorytmy grafowe Zagadnienia przedstawiane jako problemy grafowe Inne zagadnienia |
Przeszukiwanie w głąb (ang. Depth-first search, w skrócie DFS) – jeden z algorytmów przeszukiwania grafu. Przeszukiwanie w głąb polega na badaniu wszystkich krawędzi wychodzących z podanego wierzchołka. Po zbadaniu wszystkich krawędzi wychodzących z danego wierzchołka algorytm powraca do wierzchołka, z którego dany wierzchołek został odwiedzony[1].
Spis treści |
Przykład [edytuj]
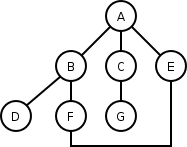
Gdybyśmy podany na obrazku graf chcieli przejść wykorzystując algorytm przeszukiwania w głąb, zaczynająć od wierzchołka A, to węzły zostałyby odwiedzone w następującej kolejności (w nawiasach podano wierzchołki do których algorytm powraca): A, B, D, (B), F, E, (F), (B), (A), C, G, (C), (A).
Algorytm [edytuj]
funkcja VisitNode(u):
kolor[u] = SZARY
czas = czas + 1
poczatek[u] = czas
dla każdego wierzchołka v na liście sąsiedztwa u:
jeżeli v jest biały:
rodzic[v] = u
VisitNode(v)
kolor[u] = CZARNY
czas = czas + 1
koniec[u] = czas
function DepthFirstSearch(Graf G):
dla każdego wierzchołka u z grafu G:
kolor[u] = BIAŁY
poczatek[u] = koniec[u] = 0
rodzic[u] = NIL
czas = 0
dla każdego wierzchołka u z grafu G:
jeżeli u jest biały:
VisitNode(u)
Właściwości [edytuj]
Złożoność pamięciowa [edytuj]
Złożoność pamięciowa przeszukiwania w głąb w przypadku drzewa jest o wiele mniejsza niż przeszukiwania wszerz, gdyż algorytm w każdym momencie wymaga zapamiętania tylko ścieżki od korzenia do bieżącego węzła, podczas gdy przeszukiwanie wszerz wymaga zapamiętywania wszystkich węzłów w danej odległości od korzenia, co zwykle rośnie wykładniczo w funkcji długości ścieżki.
Złożoność czasowa [edytuj]
Złożoność czasowa algorytmu jest uzależniona od liczby wierzchołków oraz liczby krawędzi. Algorytm musi odwiedzić wszystkie wierzchołki oraz wszystkie krawędzie, co oznacza, że złożoność wynosi O(|V|+|E|)[1].
Zupełność (kompletność) [edytuj]
Algorytm jest zupełny (czyli znajduje rozwiązanie lub informuje, że ono nie istnieje) dla drzew skończonych. Grafy skończone wymagają oznaczania już odwiedzonych wierzchołków. Dla grafów nieskończonych nie jest zupełny.
Zastosowania algorytmu [edytuj]
Algorytm stosowany jest[1]:
- do wyznaczania silnych spójnych składowych grafu skierowanego
- w algorytmie sortowania topologicznego skierowanego grafu acyklicznego
- sprawdzania, czy istnieje ścieżka między dwoma wierzchołkami w grafie (badanie spójności grafu).
Ponadto algorytm ten jest często spotykany w rozwiązaniach typu brute force problemów z innych dziedzin. Bazuje na nim zdecydowana większość algorytmów służących do przeglądania drzewa gry, np. min-max, czy też alpha-beta[potrzebne źródło].
Implementacja [edytuj]
Przypisy
- ↑ 1,0 1,1 1,2 Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Wprowadzenie do algorytmów.. Wyd. 8. Wydawnictwa Naukowo-Techniczne, 2007, s. 549-558. ISBN 978-83-204-3328-9.
