Graf regularny

Niniejszy artykuł jest częścią cyklu teoria grafów.

Najważniejsze pojęcia graf drzewo podgraf cykl klika stopień wierzchołka stopień grafu dopełnienie grafu obwód grafu pokrycie wierzchołkowe liczba chromatyczna indeks chromatyczny izomorfizm grafów homeomorfizm grafów więcej... Wybrane klasy grafów graf pełny graf spójny drzewo graf dwudzielny graf regularny graf eulerowski graf hamiltonowski graf planarny więcej... Algorytmy grafowe A* Bellmana-Forda Dijkstry Fleury'ego Floyda-Warshalla Johnsona Kruskala Prima przeszukiwanie grafu – wszerz – w głąb najbliższego sąsiada Zagadnienia przedstawiane jako problemy grafowe problem komiwojażera problem chińskiego listonosza problem marszrutyzacji problem kojarzenia małżeństw Inne zagadnienia kod Graya diagram Hassego kod Prüfera

Graf regularny stopnia $n$ to graf, w którym wszystkie wierzchołki są stopnia $n$, czyli z każdego wierzchołka grafu regularnego wychodzi $n$ krawędzi. Graf regularny stopnia $n$ określa się dla wygody mianem grafu $n$-regularnego. Szczególnym przypadkiem grafów regularnych są grafy kubiczne (grafy $3$-regularne).

• 

  graf 0-regularny

• 

  graf 1-regularny

• 

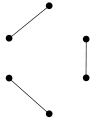
  graf 2-regularny

Znane grafy i klasy grafów regularnych

• grafy kubiczne, żmirłacze
• grafy pełne
• grafy silnie regularne
• graf Petersena

Graf silnie regularny

Graf silnie regularny to graf regularny w którym wszystkie pary sąsiadujących ze sobą wierzchołków mają tyle samo wspólnych sąsiednich wierzchołków, i wszystkie pary niesąsiadujacych ze sobą wierzchołków też mają tyle samo wspólnych wierzchołków sąsiednich.

Znane grafy i klasy grafów silnie regularnych

• graf Petersena

Linki zewnętrzne

• Grafy regularne - MathWorld
• Grafy silnie regularne - Math World