Graf (matematyka)
Graf – podstawowy obiekt rozważań teorii grafów[1][2], struktura matematyczna służąca do przedstawiania i badania relacji między obiektami[3][4]. W uproszczeniu graf to zbiór wierzchołków, które mogą być połączone krawędziami w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków[5].
Wierzchołki grafu mogą być numerowane i czasem stanowią reprezentację jakichś obiektów, natomiast krawędzie mogą wówczas obrazować relacje między takimi obiektami[6]. Wierzchołki należące do krawędzi nazywane są jej końcami[7]. Krawędzie mogą mieć wyznaczony kierunek, a graf zawierający takie krawędzie nazywany jest grafem skierowanym[8] lub orgrafem[9]. Krawędź grafu może posiadać wagę, to znaczy przypisaną liczbę, która określa na przykład odległość między wierzchołkami (jeśli np. graf jest reprezentacją połączeń między miastami)[10]. W grafie skierowanym wagi mogą być zależne od kierunku przechodzenia przez krawędź (np. jeśli graf reprezentuje trud poruszania się po jakimś terenie, to droga pod górkę będzie miała przypisaną większą wagę niż z górki)[11].
Za pierwszego teoretyka i badacza grafów uważa się[12] szwajcarskiego matematyka i fizyka Leonarda Eulera, który rozstrzygnął zagadnienie mostów królewieckich. Pierwsze użycie określenia „graf” przypisywane jest Jamesowi Josephowi Sylvesterowi – matematykowi angielskiego pochodzenia[13].
Zastosowanie grafów[edytuj | edytuj kod]
Za najstarszy przykład zastosowania grafów w rozwiązaniu zadanego problemu uznaje się[12] zagadnienie mostów królewieckich, opis którego opublikował w 1736 roku Leonhard Euler[15]:
Grafy mogą służyć do praktycznych zastosowań (także z pomocą komputerów)[16] w wielu różnorodnych problemach[8][17], np.: sieć dróg z wierzchołkami reprezentującymi skrzyżowania i krawędziami przedstawiającymi ulice[8], sieć pomieszczeń i korytarzy w budynkach[18], dzięki czemu możliwe jest komputerowe wynajdywanie najlepszej drogi ze swojego obecnego położenia do pożądanego celu. Algorytmy grafowe stanowią istotną część programów obsługujących urządzenia GPS[19]. System sztucznej inteligencji w niektórych grach komputerowych musi odszukać dla sterowanych przez program postaci najlepszą drogę, która pozwoli zaatakować przeciwnika. Zagadnienie to może być rozwiązane w oparciu o własności grafów[20]. Przedstawienie w formie grafów sieci komputerowych pozwala na stworzenie oprogramowania usprawniającego trasowanie w Internecie. W dużych organizacjach realizację zlecanych przez klientów zadań można przedstawić w postaci grafów, dzięki czemu możliwe jest zwiększenie wydajności: wierzchołki mogą reprezentować pracowników, a krawędzie grafu – przepływ zadań[21]. Za pomocą związanych z grafami pojęć można opisywać też m.in. rysunki obwodów, schematy blokowe, ponieważ przedstawiają one połączenia lub relacje, zachodzące między różnymi fragmentami wykresu[8].
Drzewa grafowe przydatne są w praktycznej reprezentacji różnego rodzaju hierarchii[22]. Mistrzostwa sportowe czy drzewo genealogiczne mogą być w przejrzysty sposób opisane przez drzewa binarne[19]. Do tworzenia kodów Huffmana można wykorzystać drzewa binarne z wagami[23]. Idea działania danego niedeterministycznego automatu skończonego może być w przejrzysty sposób pokazana przez odpowiedni graf[24].
Wzrasta również znaczenie i wykorzystanie teorii grafów w dziedzinach takich, jak chemia, lingwistyka, geografia, architektura i inne[16].
Definicje[edytuj | edytuj kod]




Różni autorzy stosują bardzo odmienne sposoby definiowania i oznaczania elementów grafu[7][27].
Graf[edytuj | edytuj kod]
Jedną z definicji grafu jest: graf (nieskierowany) składa się z dwóch zbiorów: oraz przy czym jest niepustym zbiorem, którego elementy nazywane są wierzchołkami, a jest rodziną dwuelementowych podzbiorów zbioru wierzchołków zwanych krawędziami[28]: Definicja ta nie wymaga, by i były skończone. W praktyce rozważa się także grafy o nieskończonej liczbie wierzchołków – wtedy liczba krawędzi może być zarówno skończona, jak i nieskończona[7].
Graf skierowany[edytuj | edytuj kod]
Graf skierowany lub inaczej digraf[8] składa się z dwóch zbiorów – niepustego zbioru wierzchołków oraz rodziny par uporządkowanych elementów zbioru zwanych krawędziami lub łukami grafu skierowanego. Kolejność wierzchołków w parze wyznacza kierunek krawędzi – w przypadku pary łuk biegnie z wierzchołka do wierzchołka [29]. Podobnie, jak w przypadku grafu nieskierowanego, definicja ta ma sens zarówno wtedy, gdy zbiory lub są skończone, jak i nieskończone[30].
Graf mieszany[edytuj | edytuj kod]
Graf mieszany to uporządkowana trójka grafu gdzie zbiory są zdefiniowane jak wyżej, czyli zawiera jednocześnie krawędzie skierowane i nieskierowane[31].
Grafy z wagami[edytuj | edytuj kod]
Przez zdefiniowanie funkcji z lub w pewien zbiór można przypisać krawędziom lub wierzchołkom etykiety, służące do przechowywania dodatkowych informacji[32]. Etykiety liczbowe są często nazywane wagami[33], a graf grafem z wagami (grafem z ważeniem, grafem ważonym).
W grafie ważonym krawędziowo zbiór tworzący graf jest rozszerzony o funkcję taką, że dla każdej krawędzi jest wagą danej krawędzi[11].
Grafem ważonym wierzchołkowo nazywa się graf w którym jest funkcją przypisującą każdemu wierzchołkowi pewną liczbę naturalną nazywaną wagą wierzchołka. Graf taki oznacza się przez (lub po prostu a to, że jest ważony wynika z kontekstu), natomiast wagę wierzchołka oznacza się przez [34].
Warianty definicji[edytuj | edytuj kod]
W wielu zastosowaniach podstawowe definicje grafów nie są wystarczające, dlatego wprowadza się pewne modyfikacje[7]. Na przykład aby wprowadzić pętlę, czyli krawędź, której oba końce są tym samym wierzchołkiem, w definicji grafu nieskierowanego należy dopuścić zbiory jednoelementowe [27] albo użyć dwuelementowego multizbioru W grafie skierowanym pętla jest naturalnie reprezentowana przez parę [7].
Czasami potrzebna jest możliwość połączenia dwóch wierzchołków przy pomocy więcej niż jednej krawędzi (w przypadku grafu skierowanego chodzi o łuki o takim samym zwrocie). Graf, który na to pozwala, nazywany jest multigrafem[35]. Uzyskuje się go np. przez zdefiniowanie lub jako multizbioru[7].
- Przykłady odmiennych sposobów definiowania grafu
Graf może być też określony jako niepusty zbiór wierzchołków i dana na nim relacja binarna taka, że dla dowolnych wierzchołków i zachodzi wtedy i tylko wtedy, gdy istnieje krawędź łącząca i [30]. Dla grafów nieskierowanych relacja ta jest symetryczna[36].
Graf nieskierowany można też definiować[7] jako trójkę gdzie jest niepustym zbiorem, którego elementy nazywają się wierzchołkami, jest rodziną dwuelementowych podzbiorów zbioru wierzchołków zwanych krawędziami: a jest funkcją ze zbioru w zbiór wszystkich podzbiorów jedno- lub dwuelementowych zbioru Wówczas jeżeli jest krawędzią grafu, to kończy się ona wierzchołkami gdy i jest pętlą wierzchołka gdy
Graf skierowany określa się też jako trójkę gdzie zbiory i są zdefiniowane analogicznie do grafów nieskierowanych a jest funkcją ze zbioru krawędzi w zbiór uporządkowanych par (kwadrat kartezjański, czyli iloczyn kartezjański zbioru ze sobą) wierzchołków – Jeśli jest krawędzią grafu oraz to nazywane jest początkiem krawędzi a – końcem krawędzi i mówi się, że biegnie od do [30].
Inne typy grafów[edytuj | edytuj kod]
Grafy nieskończone[edytuj | edytuj kod]
Formalne definicje grafu nie wymagają, by zbiory krawędzi czy wierzchołków były skończone, jednak w literaturze źródłowej zazwyczaj przyjmuje się uproszczenie, że zbiory oraz są skończone[30][38].
W przypadku nieskończonego zbioru wierzchołków przy skończonej ilości krawędzi otrzymuje się graf o nieskończonej ilości wierzchołków izolowanych. W przypadku skończonej ilości wierzchołków i nieskończonej ilości krawędzi otrzyma się graf o nieskończonej ilości pętli lub krawędzi wielokrotnych. W obu przypadkach są to grafy skończone. Graf nieskończony składa się z nieskończonego zbioru wierzchołków oraz nieskończonej rodziny krawędzi grafu. Gdy zarówno jak i są przeliczalne, graf nazywa się grafem przeliczalnym. Wiele pojęć z zakresu własności grafów (np. ścieżka[37], planarność, spójność[38]) można z powodzeniem rozszerzyć na grafy nieskończone. Do grafów nieskończonych należą m.in.:
- graf lokalnie skończony – graf nieskończony, którego każdy wierzchołek posiada skończony stopień,
- graf lokalnie przeliczalny – graf nieskończony, którego każdy wierzchołek ma przeliczalny stopień[38].
Graf abstrakcyjny[edytuj | edytuj kod]
Jeśli nazwać węzłami elementy niepustego zbioru to dla każdej pary węzłów zachodzi jeśli są elementami iloczynu kartezjańskiego (są wtedy nierozróżnialne). Gdy są elementami zbioru wtedy wprowadza się między nimi rozróżnienie. Dodatkowo niech będzie zbiorem, który może być pusty, a którego elementy nazywane będą połączeniami. Abstrakcyjny graf (ukierunkowany lub nieukierunkowany) jest zadany strukturą matematyczną ze zbiorami węzłów połączeń oraz odwzorowaniem incydentnym zdefiniowanym pomiędzy połączeniami oraz parami nierozróżnialnych węzłów lub rozróżnialnych [39].
Graf geometryczny[edytuj | edytuj kod]
Dla każdego grafu istnieje nieskończenie wiele[40] przedstawiających go rysunków[41], gdyż klasyczne definicje grafów nie uwzględniają pojęć z zakresu geometrii, takich jak miara kątów, długości odcinków itp[40]. Czasami jednak rozważane są w przypadku grafów własności stricte geometryczne (współrzędne geometryczne wierzchołków, tylko proste krawędzie, zmieszczenie się w pewnej przestrzeni itp.)[40][42]. Grafy, rozpatrywane jako figury w przestrzeni (w której są one „zanurzone” i która nadaje im cechy charakterystyczne dla danej przestrzeni), nazywa się grafami geometrycznymi[40][43]. Nadanie grafom właściwości geometrycznych może odbyć się, na przykład, poprzez wprowadzenie długości krawędzi jako spełniającej postulaty metryki dwuargumentowej funkcji ze zbioru krawędzi grafu w zbiór dodatnich liczb rzeczywistych[44].
Pojęcia służące do opisu grafów[edytuj | edytuj kod]





Alfabetyczna lista definicji[edytuj | edytuj kod]
- Acentryczność wierzchołka grafu – maksymalna odległość wierzchołka do innych wierzchołków grafu[48] lub inaczej długość najdłuższej ścieżki prostej zaczynającej się w danym wierzchołku[49].
- Automorfizm grafu – wzajemnie jednoznaczne przekształcenie zbioru wierzchołków grafu prostego w ten sam zbiór takie, że wierzchołki oraz są sąsiednie wtedy i tylko wtedy, gdy i są sąsiednie[50].
- Centrum grafu – wierzchołek grafu spójnego taki, że największa z odległości od centrum do innych wierzchołków grafu jest najmniejsza[51].
- Cykl – zamknięta droga prosta taka że krawędź kończy się w początkowym wierzchołku drogi[52].
- Droga – wyznaczona przez krawędzie trasa, polegająca na podróżowaniu od wierzchołka do wierzchołka po łączących je krawędziach[52]. Jeżeli przez oznaczy się -tą krawędź grafu, to droga może być jednoznacznie zapisana jako [53][54].
- Droga prosta – droga niezawierająca dwóch tych samych krawędzi[55].
- Długość drogi/ścieżki – liczba krawędzi/wierzchołków, tworzących daną drogę/ścieżkę[56].
- Droga acykliczna – droga, niezawierająca cyklu[52].
- Drzewo spinające grafu – spójny, acykliczny podgraf danego grafu, zawierający wszystkie jego wierzchołki[53].
- Gęstość grafu – stosunek liczby krawędzi do największej możliwej liczby krawędzi[57]. Używa się również określeń: graf gęsty, jeżeli ma on dużo krawędzi w stosunku do liczby wierzchołków, i podobnie graf rzadki, jeżeli ma on mało krawędzi w stosunku do liczby wierzchołków, przy czym znaczenie słów mało i dużo może zależeć od kontekstu[58].
- Klika – podzbiór wierzchołków danego grafu wraz z krawędziami je łączącymi, takich, że każde dwa wierzchołki tego podzbioru są sąsiadami[59][60] (czyli podgraf pełny[61]).
- Kolorowanie grafu – nadanie każdemu wierzchołkowi koloru tak, by żadne sąsiadujące ze sobą wierzchołki nie były pokolorowane tym samym kolorem[62].
- Krawędzie sąsiednie – krawędzie kończące się w jednym wierzchołku[63]. W przypadku grafów skierowanych zazwyczaj wymagana jest zgodność kierunków krawędzi, tj. dwie krawędzie są sąsiednie, jeżeli odpowiednio kończą się i zaczynają w tym samym wierzchołku[52].
- Krawędź/wierzchołek krytyczny – krawędź/wierzchołek, po usunięciu której/którego ze zbioru pokrywającego zmniejsza się indeks pokrycia krawędziowego/wierzchołkowego[64].
- Liczba chromatyczna – najmniejsza liczba kolorów potrzebna do prawidłowego pokolorowania grafu[62].
- Most – krawędź, po usunięciu której wzrasta liczba spójnych składowych grafu[65].
- Nadgraf grafu – taki graf, że jest jego podgrafem[66].
- Odległość – liczba krawędzi w najkrótszej ścieżce łączącej dane dwa wierzchołki.
- Pętla – krawędź zaczynająca i kończąca się w tym samym wierzchołku[7].
- Podgraf grafu – graf uzyskany poprzez usunięcie części wierzchołków z wraz z kończącymi się w nich krawędziami[67].
- Rozmiar grafu – liczbę krawędzi grafu, oznaczonych [68].
- Rząd grafu – liczba wierzchołków grafu, oznaczonych [68].
- Graf r-regularny – graf, w którym każdy wierzchołek grafu jest stopnia [69].
- Sąsiad – dwa wierzchołki są sąsiadami, jeśli istnieje krawędź pomiędzy nimi[52].
- Spójna składowa grafu – możliwie największy spójny podgraf grafu Graf spójny ma jedną spójną składową[46].
- Stopień wierzchołka – liczba kończących się w wierzchołku krawędzi[70]. Oznaczenie: [70]. W przypadku grafów skierowanych mówi się o stopniach wejściowym i wyjściowym – [71]
- Ściana – obszar zamknięty, wyznaczony przez krawędzie grafu (tzw. krawędzie tworzące ścianę)[47]. Z pojęciem ściany ściśle powiązane jest twierdzenie Eulera[72]. Za ścianę uważa się też nieskończony obszar znajdujący się na zewnątrz grafu (a więc każdy graf ma co najmniej jedną ścianę)[47].
- Ścieżka – intuicyjnie jest bardzo podobna do drogi, z tym, że jest wyznaczona przez wierzchołki, tj. można ją opisać poprzez ciąg wierzchołków [56][73].
- Ścieżka prosta – ścieżka wyznaczona tak, by żaden wierzchołek na trasie nie powtarzał się[74].
- Ścieżka zamknięta – ścieżka czyli kończąca się w początkowym wierzchołku[67].
- Usunięcie wierzchołka – wymazanie wierzchołka oraz wszystkich kończących się w nim krawędzi z danego grafu[75].
- Waga krawędzi – wartość przypisana każdej krawędzi. Często od grafu reprezentującego np. sieć połączeń komunikacyjnych oczekuje się nie tylko informacji o istniejącym połączeniu (krawędzi lub ścieżki), ale też np. o długości połączenia[10]. Graf taki można wykorzystać np. do wyznaczenia optymalnej ścieżki – w sensie przejechanych kilometrów trasy – lub ogólniej do rozwiązania problemu komiwojażera – wyznaczenia optymalnego rozłożenia kabli w sieci[17], koordynowania wysyłania plików metodą peer-to-peer itp.[2]
- Wierzchołek izolowany – wierzchołek o stopniu czyli niebędący końcem żadnej krawędzi[76].
- Wierzchołek pokrywający krawędź – wierzchołek pokrywa krawędź jeżeli kończy się w W analogiczny sposób definiuje się krawędź pokrywającą dany wierzchołek – krawędź kryje wierzchołek gdy się w nim kończy. Minimalny pokrywający podzbiór krawędzi/wierzchołków – możliwie najmniejszy podzbiór krawędzi/wierzchołków grafu taki, że pokrywają one wszystkie wierzchołki/krawędzie danego grafu. Liczność minimalnego zbioru pokrywającego krawędzi/wierzchołków nazywa się indeksem pokrycia wierzchołkowego/krawędziowego. Wszystkie podzbiory o tej liczności i własności nazywa się pokryciem minimalnym.
- Wierzchołek rozcinający – wierzchołek, po usunięciu którego zwiększa się liczba spójnych składowych grafu[77]. Nazywany przegubem tworzy tzw. wąskie gardło grafu, tj. istnieją w grafie dwa wierzchołki takie, że każda łącząca je droga musi przejść przez wierzchołek rozcinający[78].
Oznaczenia formalne[edytuj | edytuj kod]
Często dla danego grafu stosuje się skrócone oznaczenia oparte na alfabecie greckim oraz łacińskim[79][80]:
- lub – liczba wierzchołków [8][80],
- lub – liczba krawędzi [30][80],
- – najmniejszy stopień wierzchołka w [81],
- – największy stopień wierzchołka w [80],
- – liczba chromatyczna [82],
- – indeks chromatyczny [82],
- – liczba spójnych składowych [80].
- Przykład dla grafu nieskierowanego

Przykładową ścieżką prostą może być a cyklem – Stopnie wierzchołków są następujące:
Krawędź jest sąsiednia z ale nie jest z Graf ma trzy ściany – zewnętrzną oraz dwie wyznaczone odpowiednio przez ścieżki np. i Graf jest spójny, czyli ma jedną spójną składową. Natomiast podgraf grafu składający się z wierzchołków i incydentnych z nimi krawędziami ma dwie spójne składowe – cykl i wierzchołek izolowany
Izomorfizm i homeomorfizm grafów[edytuj | edytuj kod]


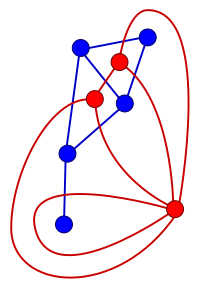
Graficzna reprezentacja grafów (w postaci kropek i łączących je krzywych) jest tylko sposobem przedstawienia relacji zachodzących między wierzchołkami. Dla każdego grafu istnieje nieskończenie wiele[40] przedstawiających go jednoznacznie wykresów, rysunków[41]. Właściwości grafów są niezależne od sposobu numerowania wierzchołków, kolejności ich rysowania itp. Grafy różniące się tylko sposobem ich przedstawienia lub indeksami nadanymi wierzchołkom nazywają się izomorficznymi[84].
Dwa grafy są homeomorficzne, jeśli z jednego grafu można otrzymać drugi, zastępując wybrane krawędzie łańcuchami prostymi lub łańcuchy proste pojedynczymi krawędziami[85].
Klasy grafów[edytuj | edytuj kod]
Grafy można podzielić ze względu na różne własności, zazwyczaj zachowane w obrębie izomorfizmów danego grafu[2][41]. Niektóre klasy grafów to:
- drzewo – spójny graf acykliczny[18],
- graf acykliczny – graf niezawierający żadnej drogi zamkniętej[89],
- graf cykliczny – regularny graf spójny, którego każdy wierzchołek jest stopnia drugiego[86],
- graf dwudzielny – graf, którego wierzchołki mogą być podzielone na dwa zbiory, tak by w obrębie jednego zbioru żaden wierzchołek nie był połączony z innym[90],
- graf dwudzielny pełny – graf dwudzielny taki, że każdy wierzchołek z jednego zbioru jest połączony krawędzią z każdym wierzchołkiem ze zbioru drugiego. Pełny graf dwudzielny o wierzchołkach oznacza się [90],
- graf eulerowski – graf, posiadający drogę prostą, przechodzącą przez każdą krawędź[91]; niebędącym grafem eulereowskim jest graf półeulerowski, w którym istnieje droga, zawierająca każdą krawędź danego grafu,
- graf genusu – graf, który można narysować bez przecięć (czyli w formie grafu płaskiego) na powierzchni genusu ale nie można narysować go bez przecięć na powierzchni genusu [92].
- graf hamiltonowski – graf, posiadający ścieżkę prostą, przechodzącą przez każdy wierzchołek[91],
- graf k-dzielny – graf, którego zbiór wierzchołków można podzielić na parami rozłącznych podzbiorów takich, że żadne dwa węzły, należące do tego samego zbioru, nie są połączone krawędzią[93],
- graf k-dzielny pełny – graf, którego zbiór wierzchołków dzieli się na niepołączonych między sobą podzbiorów wierzchołków, oraz każdy wierzchołek z -tego przedziału jest połączony z każdym wierzchołkiem z każdego z przedziałów poza [93],
- graf k-spójny – graf, posiadający spójnych składowych[94],
- graf komórkowy – graf płaski, którego wszystkie ściany są utworzone przez drogi zamknięte tej samej długości[95],
- graf krytyczny – graf, którego każdy wierzchołek/krawędź jest krytyczny/krytyczna[78],
- graf kubiczny – specjalne określenie dla grafów regularnych stopnia [96],
- graf liniowy – graf, otrzymany poprzez usunięcie jednej krawędzi z grafu cyklicznego[86],
- graf pełny – graf, którego każdy wierzchołek jest połączony bezpośrednio krawędzią z każdym innym[97]; graf pełny o wierzchołkach oznacza się [86][69],
- graf planarny – graf, dla którego istnieje graf izomorficzny i który można przedstawić na płaszczyźnie tak, by żadne krawędzie się nie przecinały[98]. Kazimierz Kuratowski udowodnił, że grafy pełne i są nieplanarne oraz że każdy inny graf nieplanarny musi posiadać podgraf homeomorficzny z którymś z tych grafów[83],
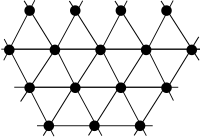
- graf platoński – grafy, utworzone z krawędzi i wierzchołków wielościanów foremnych[99],
- graf płaski – izomorficzne przedstawienie grafu takie, że żadne dwie krawędzie się nie przecinają[100],
- graf podstawowy grafu skierowanego – niemal ten sam, co graf płaski, ale nieskierowany, bo bez zwrotów na krawędziach[101],
- graf prosty – graf, niezawierający pętli ani krawędzi wielokrotnych[102], nazywany jest multigrafem[97]; z reguły zdanie „ jest grafem” oznacza w domyśle, że jest grafem prostym[7],
- graf przedziałowy – graf, utworzony ze zbioru odcinków na prostej poprzez przypisanie każdemu odcinkowi wierzchołka i połączenie krawędziami wierzchołków, których odcinki się nakładają[103],
- graf pusty – graf, nieposiadający krawędzi[104],
- graf r-regularny – graf, którego każdy wierzchołek jest stopnia [69],
- graf samodopełniający – graf prosty izomorficzny ze swoim własnym dopełnieniem,
- graf spójny – graf, w którym dla każdego wierzchołka istnieje droga do każdego innego wierzchołka[46],
- graf toroidalny – graf genusu [92],
- k-kostka – regularny graf dwudzielny, którego wierzchołki odpowiadają ciągom że i którego wierzchołki połączone są krawędzią wtedy i tylko wtedy, gdy różnią się jednym wyrazem odpowiadającego im ciągu[87],
- koło – graf o wierzchołkach, utworzony z grafu cyklicznego o wierzchołkach poprzez połączenie nowego wierzchołka z każdym wierzchołkiem w grafie cyklicznym[86],
- las – niespójny graf acykliczny[105],
- turniej – graf skierowany, w którym każde dwa wierzchołki łączy dokładnie jedna krawędź[106].
Operacje na grafach[edytuj | edytuj kod]
Operacje binarne[edytuj | edytuj kod]
- Suma grafów
– jeżeli dane są dwa grafy oraz to ich sumą jest graf, którego zbiór wierzchołków i krawędzi tworzą wszystkie wierzchołki i krawędzie tych grafów[108].
- Przecięcie grafów
Przecięcie grafów [109] jest definiowane analogicznie do sumy. Jeżeli dane są dwa grafy i to ich przecięciem jest graf, którego wierzchołki i krawędzie wchodzą w skład obu tych grafów[110].
- Zespolenie grafów
– zespoleniem grafów i nazywa się graf, w którym z każdego wierzchołka poprowadzono krawędzie do każdego wierzchołka [111].
Operacje unarne[edytuj | edytuj kod]
- Graf krawędziowy
Graf krawędziowy grafu prostego to graf, który dla każdej krawędzi z ma wierzchołek połączony z wierzchołkami reprezentującymi pozostałe krawędzie sąsiadujące ze sobą w [112]. Etapy konstrukcji grafu krawędziowego
- Jeśli każdej krawędzi grafu przypisać jednoznacznie węzeł grafu to
- Dwa węzły grafu oraz da się połączyć krawędzią wtedy i tylko wtedy, gdy odpowiednie krawędzie oraz w grafie są do siebie przyległe, tj. kończą się w jednym wierzchołku[113].
- Dopełnienie grafu
Dopełnieniem grafu nazywa się graf w którym dwa wierzchołki są sąsiednie wtedy i tylko wtedy, gdy nie były sąsiednie w Inaczej mówiąc, w dopełnieniu dwa wierzchołki są połączone krawędzią wtedy, gdy nie były połączone w grafie wyjściowym[87].
- Graf dualny
Graf dualny grafu – graf, którego wierzchołki odpowiadają ścianom w Wierzchołki te są połączone, jeżeli odpowiednie ściany w są sąsiednie[114].
- Domknięcie przechodnie
Domknięcie przechodnie dowolnych wierzchołków grafu następuje wtedy i tylko wtedy, gdy pomiędzy wierzchołkami grafu, posiadającego te same wierzchołki co istnieje droga[115].
Algorytmy grafowe[edytuj | edytuj kod]
Poprzez pojęcie algorytmu grafowego rozumie się zazwyczaj algorytmy rozwiązujące problemy przedstawione przy użyciu pojęcia grafu[2][116].
Przeszukiwanie grafu[edytuj | edytuj kod]
Przez przeszukiwanie lub przechodzenie grafu rozumie się ciąg czynności, polegających na odwiedzeniu w jakiś usystematyzowany sposób wszystkich wierzchołków grafu w celu zebrania potrzebnych informacji[117]. Często podczas przejścia grafu rozwiązuje się już jakiś problem, ale przeważnie jest to tylko wstęp do wykonania właściwego algorytmu grafowego[118]. Najczęściej używane metody przeszukiwania grafów:
- Przeszukiwanie wszerz
Przeszukiwanie wszerz polega na odwiedzeniu wszystkich wierzchołków, osiągalnych z danego wierzchołka[119].
- Przeszukiwanie w głąb
Przeszukiwanie w głąb polega na badaniu wszystkich krawędzi, wychodzących z podanego wierzchołka. Po zbadaniu wszystkich krawędzi wychodzących z danego wierzchołka algorytm powraca do wierzchołka, z którego dany wierzchołek został odwiedzony[120].
Sposoby prezentacji grafów[edytuj | edytuj kod]
Każdy graf może być jednoznacznie prezentowany na wiele sposobów. Dla percepcji człowieka najwygodniejszy jest rysunek grafu[121], pozostałe sposoby prezentacji wykorzystywane są w komputerach[35][122]. Każda z tych prezentacji ma swoje wady i zalety, generalnie ograniczające są dwa warunki – ilość pamięci przeznaczonej na prezentację i jej możliwości szybkiego odpowiadania na pytania, czy między wierzchołkami i jest krawędź[123]. W przypadku grafów rzadkich listy sąsiedztwa okazują się wystarczająco szybkie by zrezygnować z pamięciożernych tablic[124]. Sposobami prezentacji grafów są: rysunek, macierze sąsiedztwa, listy sąsiedztwa[118] i macierze incydencji[125].
Rysunek grafu[edytuj | edytuj kod]
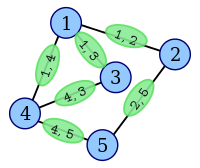
Jednym ze sposobów prezentacji grafu jest rysunek grafu, ukazujący wierzchołki i łączące je krawędzie[35]. Wierzchołki oznaczane są zazwyczaj kropkami[30] lub kołami[9], niekiedy zawierającymi indeksy bądź inne dodatkowe informacje[2][126]. Krawędzie prezentowane są krzywymi[6] bądź prostymi[5], w przypadku krawędzi ważonych waga umieszczona jest bezpośrednio nad krawędzią[127].
Rysunkiem grafu jest wykres składający się z punktów odpowiadających wierzchołkom zbioru i łuków czy odcinków odpowiadających krawędziom, tak, że jeśli to łuk dla krawędzi łączy punkty oznaczone literami i
Macierz sąsiedztwa[edytuj | edytuj kod]
Jedną ze struktur danych, umożliwiających przedstawienie skomplikowanego grafu lub jego przechowywanie w pamięci komputera, jest macierz sąsiedztwa, zawierająca dane na temat połączeń między wierzchołkami. Macierz jest rozmiaru na wyraz, leżący z -tego wiersza i -tej kolumny, zawiera wartość będącą liczbą krawędzi łączących -ty i -ty wierzchołek. W przypadku grafów prostych wyrazami w macierzy będą wartości boole’owskie – jest krawędź, bądź nie ma krawędzi[128]. Macierz sąsiedztwa pozwala na prezentację grafów, zawierających krawędzie wielokrotne oraz pętle własne. Aby dowiedzieć się, ile krawędzi łączy wierzchołki wystarczy sprawdzić wartość komórki [129]. Tak zaimplementowana komputerowa struktura danych gwarantuje, że operacje sprawdzenia, czy dodania oraz usunięcia krawędzi odbywają się w stałym czasie. Do jej wad należy duża ilość potrzebnej pamięci (asymptotyczne tempo wzrostu [130]) oraz fakt, że czas potrzebny do przejrzenia zbioru krawędzi jest proporcjonalny do kwadratu liczby wierzchołków (złożoność obliczeniowa wynosi ), zamiast do liczby krawędzi[129].
| Macierz sąsiedztwa | Rys. |
|---|---|
|
|
 |
Lista sąsiedztwa[edytuj | edytuj kod]
Drugą popularną reprezentacją grafu są tzw. listy sąsiedztwa – dla każdego wierzchołka zapamiętywana jest lista sąsiadujących z nim wierzchołków. W implementacji tej metody stosuje się listy jednokierunkowe oraz jednowymiarową tablicę wskaźników o rozmiarze gdzie -ty element tablicy jest wskaźnikiem do początku listy przechowującej sąsiadów -tego wierzchołka[131]. W odróżnieniu od macierzy sąsiedztwa lista sąsiedztwa wymaga ilości pamięci proporcjonalnej do liczby krawędzi[130], także przejrzenie całego zbioru krawędzi jest proporcjonalne do jego rozmiaru. W stosunku do macierzy sąsiedztwa większą złożoność mają jednak operacje elementarne – sprawdzenie, czy wymaga czasu proporcjonalnego do mniejszego ze stopni wierzchołków, a np. usunięcie krawędzi – do większego z nich[132][133].
| Lista sąsiedztwa | Rys. |
|---|---|
|
|
 |
Macierz incydencji[edytuj | edytuj kod]
Macierz incydencji wymiaru na zawiera informacje takie, że tylko, gdy -ta krawędź kończy się w -tym wierzchołku (czyli jest z nim incydentna)[125]. W przeciwnym wypadku [125]. Jeśli oznaczyć krawędzie przykładowego grafu tak jak na jego rysunku, to macierz incydencji o kolumnach odpowiadającym krawędziom i wierszach odpowiadającym wierzchołkom może wyglądać następująco[122]:
| Macierz incydencji | Rys. |
|---|---|
|
|
 |
Uogólnienia[edytuj | edytuj kod]

- Hipergrafy
Hipergraf jest strukturą podobną do grafu[134], z tą różnicą, że jego krawędź może łączyć więcej niż dwa wierzchołki[135].
- Grafy w teorii modeli
W teorii modeli graf jest szczególnym przypadkiem struktury matematycznej[136].
- Grafy a matroidy
Matroidy mogą być rozważane jako uogólnienie pojęcia grafu[137], a pojęcia grafowe rozważane w odniesieniu do pojęć teorii matroidów mogą być przedstawione w prostszy sposób[138]. Niech dany będzie dowolny graf Zbiór krawędzi grafu można rozważać jako nośnik matroidu. Zbiorami niezależnymi będą te jego podzbiory, które nie zawierają cyklu, tj. drzewa oraz lasy[139].
Zobacz też[edytuj | edytuj kod]
Przypisy[edytuj | edytuj kod]
- ↑ Reinhard Diestel ↓, s. 1.
- ↑ a b c d e Adrian Horzyk ↓.
- ↑ Ramsey Young, Brian Sandall ↓.
- ↑ Graphs and Networks ↓.
- ↑ a b Robin J. Wilson ↓, s. 11.
- ↑ a b Robin J. Wilson ↓, s. 12.
- ↑ a b c d e f g h i Kenneth A. Ross, Charles R.B. Wright ↓, s. 147.
- ↑ a b c d e f Kenneth A. Ross, Charles R.B. Wright ↓, s. 142.
- ↑ a b Juliusz Lech Kulikowski ↓, s. 39.
- ↑ a b Kenneth A. Ross, Charles R.B. Wright ↓, s. 373.
- ↑ a b Robin J. Wilson ↓, s. 138.
- ↑ a b Kenneth A. Ross, Charles R.B. Wright ↓, s. 140.
- ↑ Jonathan L. Gross, Jay Yellen ↓, s. 35.
- ↑ Robin J. Wilson ↓, s. 17.
- ↑ Kenneth A. Ross, Charles R.B. Wright ↓, s. 340.
- ↑ a b Robin J. Wilson ↓, s. 7.
- ↑ a b Bohdan Korzan ↓, s. 9.
- ↑ a b Kenneth A. Ross, Charles R.B. Wright ↓, s. 352.
- ↑ a b Robert Kowalczyk ↓, s. 2.
- ↑ Robert Kowalczyk ↓, s. 2–3.
- ↑ Robert Kowalczyk ↓, s. 3.
- ↑ Kenneth A. Ross, Charles R.B. Wright ↓, s. 361.
- ↑ Thomas Cormen ↓, s. 385.
- ↑ Thomas Cormen ↓, s. 968.
- ↑ Kenneth A. Ross, Charles R.B. Wright ↓, s. 386.
- ↑ Kenneth A. Ross, Charles R.B. Wright ↓, s. 148.
- ↑ a b Robin J. Wilson ↓, s. 20.
- ↑ Graf, [w:] Encyklopedia PWN [dostęp 2021-07-22].
- ↑ Robin J. Wilson ↓, s. 135.
- ↑ a b c d e f Kenneth A. Ross, Charles R.B. Wright ↓, s. 143.
- ↑ Matthias Beck ↓, s. 1.
- ↑ Peter Fletcher ↓, s. 463.
- ↑ Robin J. Wilson ↓, s. 57.
- ↑ Rafał Witkowski ↓, s. 3.
- ↑ a b c Kenneth A. Ross, Charles R.B. Wright ↓, s. 144.
- ↑ Grażyna Mirkowska ↓.
- ↑ a b c Robin J. Wilson ↓, s. 106.
- ↑ a b c Robin J. Wilson ↓, s. 105.
- ↑ Stanisław Kaprzyk ↓.
- ↑ a b c d e Juliusz Lech Kulikowski ↓, s. 71.
- ↑ a b c Teoria grafów ↓.
- ↑ Elżbieta Lewandowicz ↓, s. 269.
- ↑ Elżbieta Lewandowicz ↓, s. 271.
- ↑ Juliusz Lech Kulikowski ↓, s. 72.
- ↑ Robin J. Wilson ↓, s. 65.
- ↑ a b c Kenneth A. Ross, Charles R.B. Wright ↓, s. 342.
- ↑ a b c Robin J. Wilson ↓, s. 89.
- ↑ Małgorzata Kuchta ↓.
- ↑ Jérémie Bouttier ↓.
- ↑ Robin J. Wilson ↓, s. 34–35.
- ↑ Robin J. Wilson ↓, s. 67.
- ↑ a b c d e Kenneth A. Ross, Charles R.B. Wright ↓, s. 146.
- ↑ a b Robin J. Wilson ↓, s. 145.
- ↑ Marek Majewski, Teoria grafów i jej zastosowania ↓, s. 13–19.
- ↑ Kenneth A. Ross, Charles R.B. Wright ↓, s. 328.
- ↑ a b Kenneth A. Ross, Charles R.B. Wright ↓, s. 145.
- ↑ Graph Theory ↓.
- ↑ Agnieszka Rybarczyk ↓.
- ↑ Juliusz Lech Kulikowski ↓, s. 264.
- ↑ Jakub Wróblewski ↓.
- ↑ Dariusz Dereniowski ↓, s. 11.
- ↑ a b Robin J. Wilson ↓, s. 110.
- ↑ Kenneth A. Ross, Charles R.B. Wright ↓, s. 150.
- ↑ Kenneth A. Ross, Charles R.B. Wright ↓, s. 496.
- ↑ Robin J. Wilson ↓, s. 44.
- ↑ Paweł Wal ↓.
- ↑ a b Kenneth A. Ross, Charles R.B. Wright ↓, s. 327.
- ↑ a b Jerzy Wałaszek, Podstawowe pojęcia dotyczące grafów ↓.
- ↑ a b c Kenneth A. Ross, Charles R.B. Wright ↓, s. 334.
- ↑ a b c Kenneth A. Ross, Charles R.B. Wright ↓, s. 333.
- ↑ Kenneth A. Ross, Charles R.B. Wright ↓, s. 483.
- ↑ Robin J. Wilson ↓, s. 90.
- ↑ Jolanta Koszelew ↓, s. 1.
- ↑ Jolanta Koszelew ↓, s. 2.
- ↑ Izolda Gorgol ↓, s. 2.
- ↑ Robin J. Wilson ↓, s. 24.
- ↑ Robin J. Wilson ↓, s. 45.
- ↑ a b Konstanty Junosza-Szaniawski ↓.
- ↑ Kenneth A. Ross, Charles R.B. Wright ↓, s. wykaz oznaczeń.
- ↑ a b c d e Robin J. Wilson ↓, s. 9.
- ↑ Stopień wierzchołka ↓.
- ↑ a b Robin J. Wilson ↓, s. 10.
- ↑ a b Robin J. Wilson ↓, s. 85.
- ↑ Robin J. Wilson ↓, s. 21.
- ↑ Robin J. Wilson ↓, s. 84.
- ↑ a b c d e f g Robin J. Wilson ↓, s. 30.
- ↑ a b c Robin J. Wilson ↓, s. 33.
- ↑ Juliusz Lech Kulikowski ↓, s. 221.
- ↑ Thomas Cormen ↓, s. 115.
- ↑ a b Kenneth A. Ross, Charles R.B. Wright ↓, s. 378.
- ↑ a b Robin J. Wilson ↓, s. 14.
- ↑ a b Robin J. Wilson ↓, s. 95–96.
- ↑ a b Pojęcia wstępne teorii grafów ↓, s. 9.
- ↑ Andrzej Ruciński ↓.
- ↑ Juliusz Lech Kulikowski ↓, s. 223.
- ↑ Robin J. Wilson ↓, s. 31.
- ↑ a b Kenneth A. Ross, Charles R.B. Wright ↓, s. 278.
- ↑ Robin J. Wilson ↓, s. 15.
- ↑ Andrzej Łachwa ↓, s. 20.
- ↑ Robin J. Wilson ↓, s. 82.
- ↑ Wojciech Palacz ↓, s. 2.
- ↑ Robin J. Wilson ↓, s. 13.
- ↑ Grafy cięciwowe, grafy przedziałowe, grafy dwudzielne ↓.
- ↑ Robin J. Wilson ↓, s. 29.
- ↑ Kenneth A. Ross, Charles R.B. Wright ↓, s. 358.
- ↑ Kenneth A. Ross, Charles R.B. Wright ↓, s. 488.
- ↑ William Kocay, Daniel Neilson, Ryan Szypowski ↓.
- ↑ Robin J. Wilson ↓, s. 22.
- ↑ Andrzej Łachwa ↓, s. 6.
- ↑ Andrzej Wiśniewski ↓.
- ↑ Marek Majewski, Własności grafów ↓, s. 5–7.
- ↑ Robin J. Wilson ↓, s. 34.
- ↑ Juliusz Lech Kulikowski ↓, s. 201–202.
- ↑ Robin J. Wilson ↓, s. 99.
- ↑ Marcin Żurawski ↓, s. 46.
- ↑ Kazimierz Jakubczyk ↓, s. 147.
- ↑ Kazimierz Jakubczyk ↓, s. 154, 157.
- ↑ a b Thomas Cormen ↓, s. 526.
- ↑ Łukasz Kowalik ↓, s. 2.
- ↑ Kenneth A. Ross, Charles R.B. Wright ↓, s. 427.
- ↑ Witold Lipski, Tomasz Czajka ↓, s. 74.
- ↑ a b c d Robin J. Wilson ↓, s. 26.
- ↑ Thomas Cormen ↓, s. 526–527.
- ↑ Thomas Cormen ↓, s. 527.
- ↑ a b c Robin J. Wilson ↓, s. 27.
- ↑ Juliusz Lech Kulikowski ↓, s. 40.
- ↑ Kenneth A. Ross, Charles R.B. Wright ↓, s. 491.
- ↑ Kenneth A. Ross, Charles R.B. Wright ↓, s. 669.
- ↑ a b Jerzy Wałaszek, Teoria grafów dla początkujących ↓.
- ↑ a b Kazimierz Jakubczyk ↓, s. 153.
- ↑ Kazimierz Jakubczyk ↓, s. 152.
- ↑ Thomas Cormen ↓, s. 528.
- ↑ Witold Lipski, Tomasz Czajka ↓, s. 77.
- ↑ Thomas Cormen ↓, s. 116.
- ↑ Bohdan Korzan ↓, s. 21–22.
- ↑ Anuj Dawar ↓.
- ↑ Thomas Cormen ↓, s. 392.
- ↑ Robin J. Wilson ↓, s. 186.
- ↑ Zofia Miechowicz ↓.
Bibliografia[edytuj | edytuj kod]
- Matthias Beck i in, On Weak Chromatic Polynomials of Mixed Graphs [online], Iowa State University of Science and Technology [dostęp 2014-05-03] [zarchiwizowane z adresu 2014-05-03].
- Jérémie Bouttier, Geodesic Distance in Planar Graphs [online], Cornell University Library.
- Thomas Cormen i in: Wprowadzenie do algorytmów. Warszawa: 2013. ISBN 978-83-01-16911-4.
- Anuj Dawar, Finite Model Theory and Graph Isomorphism [online], Computer Laboratory University of Cambridge.
- Dariusz Dereniowski, Algorytmy Grafowe – wprowadzenie [online], Wydział Elektroniki, Telekomunikacji i Informatyki Politechniki Gdańskiej.
- Reinhard Diestel: Graph Theory. Nowy Jork: 2000. ISBN 0-387-95014-1.
- Peter Fletcher, Hughes Hoyle, C. Wayne Patty: Foundations of Discrete Mathematics. Boston: 1991. ISBN 0-53492-373-9.
- Izolda Gorgol, Pojęcia wstępne teorii grafów [online], Zakład Systemów Informatycznych Politechniki Lubelskiej.
- Graphs and Networks [online], Stanford University.
- Grafy cięciwowe, grafy przedziałowe, grafy dwudzielne [online], Zespół Katedr i Zakładów Informatyki Matematycznej Uniwersytetu Jagiellońskiego [dostęp 2014-04-30] [zarchiwizowane z adresu 2014-05-02].
- Graph Theory [online], Webwhompers [dostęp 2014-04-30] [zarchiwizowane z adresu 2014-05-02].
- Jonathan L. Gross, Jay Yellen: Handbook of graph theory. Warszawa: 2004. ISBN 978-1-58488-090-5.
- Adrian Horzyk, Podstawy informatyki – grafy [online], Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie.
- Kazimierz Jakubczyk, Algorytmy grafowe [online], Kazimierz Jakubczyk [zarchiwizowane z adresu 2012-01-31].
- Konstanty Junosza-Szaniawski, Teoria grafów [online], Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej.
- Stanisław Kaprzyk, Grafy abstrakcyjne i geometryczne [online], Wykłady z dyskretnej geometrii komputerowej [dostęp 2014-04-27] [zarchiwizowane z adresu 2014-04-27].
- Bohdan Korzan: Grafy, hipergrafy i sieci. Warszawa: 1980.
- Jolanta Koszelew, Podstawowe pojęcia dotyczące grafów [online], Algorytmy i struktury danych [dostęp 2014-05-01] [zarchiwizowane z adresu 2016-01-09].
- Robert Kowalczyk, Grafy i metody ich przeszukiwania. Zastosowania [online], ydział Matematyki i Informatyki Uniwersytetu Łódzkiego [dostęp 2014-05-01] [zarchiwizowane z adresu 2014-05-02].
- Łukasz Kowalik, Algorytmy grafowe [online], Wydział Matematyki, Informatyki i Mechaniki Uniwersytetu Warszawskiego.
- Malgorzata Kuchta, Teoria grafów [online], Instytut Matematyki i Informatyki Politechniki Wrocławskiej [dostęp 2014-04-30] [zarchiwizowane z adresu 2014-05-02].
- Elżbieta Lewandowicz, Drzewa grafowe w analizach dostępności [online], CeON – Centrum Otwartej Nauki.
- Witold Lipski, Tomasz Czajka: Kombinatoryka dla programistów. Warszawa: 2004. ISBN 83-204-2968-4.
- Andrzej Łachwa, Matematyka dyskretna [online], Zakład Projektowania i Grafiki Komputerowej Uniwersytetu Jagiellońskiego.
- Marek Majewski, Teoria grafów i jej zastosowania [online], Wydział Matematyki i Informatyki Uniwersytetu Łódzkiego.
- Marek Majewski, Własności grafów [online], Wydział Matematyki i Informatyki Uniwersytetu Łódzkiego [dostęp 2014-04-30] [zarchiwizowane z adresu 2014-05-02].
- Zofia Miechowicz, Kiedy zachłanność popłaca? [online], Ośrodek Kultury Matematycznej – Szkoła Matematyki Poglądowej [dostęp 2014-04-27] [zarchiwizowane z adresu 2014-04-27].
- Grażyna Mirkowska, Algorytmy grafowe [online], Polsko-Japońska Wyższa Szkoła Technik Komputerowych.
- Wojciech Palacz, Algorytmy i struktury danych 2 [online], Zakład Projektowania i Grafiki Komputerowej Uniwersytetu Jagiellońskiego [dostęp 2014-05-01] [zarchiwizowane z adresu 2014-05-02].
- Pojęcia wstępne teorii grafów [online], V rok Wydziału Matematyczno-Przyrodniczego Uniwersytetu Kardynała Stefana Wyszyńskiego [dostęp 2014-05-01] [zarchiwizowane z adresu 2014-05-02].
- Kenneth A. Ross, Charles R.B. Wright: Matematyka dyskretna. Warszawa: 2005. ISBN 83-0114-380-0.
- William Kocay, Daniel Neilson, Ryan Szypowski, Drawing Graphs on the Torus [online], University of Manitoba [dostęp 2021-06-05] [zarchiwizowane z adresu 2017-08-29].
- Juliusz Lech Kulikowski: Zarys teorii grafów. Zastosowanie w technice. Warszawa: 1986. ISBN 83-0105-277-5.
- Andrzej Ruciński: Teoria grafów 2 (TGR 430) – wiosna 2009, Cz. 4, 2-spójność, 3-spójność. Zakład Matematyki Dyskretnej Uniwersytetu im. Adama Mickiewicza.
- Agnieszka Rybarczyk, ALG – Reprezentacje grafów [online], Instytut Informatyki Politechniki Poznańskiej.
- Stopień wierzchołka [online], Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej.
- Teoria grafów [online], Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej.
- Paweł Wal, Matematyka dyskretna [online], Paweł J. Wal [dostęp 2014-04-30] [zarchiwizowane z adresu 2014-05-01].
- Jerzy Wałaszek, Podstawowe pojęcia dotyczące grafów [online], I Liceum Ogólnokształcące im. Kazimierza Brodzińskiego w Tarnowie [dostęp 2014-05-01] [zarchiwizowane z adresu 2014-05-02].
- Jerzy Wałaszek, Teoria grafów dla początkujących. Reprezentacja grafów w pamięci komputera [online], I Liceum Ogólnokształcące im. Kazimierza Brodzińskiego w Tarnowie [dostęp 2014-05-01] [zarchiwizowane z adresu 2014-05-02].
- Robin J. Wilson: Wprowadzenie do teorii grafów. Warszawa: 1998. ISBN 83-0112-641-8.
- Andrzej Wiśniewski, Logika I. Materiały do wykładu dla studentów kognitywistyki. Wykład 2. Działania na zbiorach [online], Zakład Matematyki Dyskretnej Uniwersytetu im. Adama Mickiewicza [dostęp 2014-05-01] [zarchiwizowane z adresu 2014-05-02].
- Rafał Witkowski, Multikolorowanie grafów [online], X Międzynarodowe Warsztaty Młodych Matematyków, 2007 [dostęp 2015-11-18] [zarchiwizowane z adresu 2015-11-19].
- Jakub Wróblewski, Problemy optymalizacyjne – zastosowania [online], Jakub Wróblewski.
- Ramsey Young, Brian Sandall, Graph Theory in Drama [online], University of Colorado [dostęp 2021-06-05] [zarchiwizowane z adresu 2016-04-06].
- Marcin Żurawski, Grafy [online], Marcin Żurawski.
Linki zewnętrzne[edytuj | edytuj kod]
- Chris K. Caldwell, Graph theory tutorial [online], The University of Tennessee.
- Algorithms. Tutoring web page [online]. – Aplety obrazujące niektóre algorytmy teorii grafów.
- Łukasz Kowalik, Algorytmiczne problemy ścieżkowe w grafach planarnych. Rozprawa doktorska [online], Max Planck Institut Informatik [dostęp 2014-05-01] [zarchiwizowane z adresu 2011-08-13].


























































































































































![{\displaystyle A[i,j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1a9bfca6057f52b4e5c3844ecd704962b7e426c)


![{\displaystyle A=\left[{\begin{matrix}0&1&0&1\\1&0&1&2\\0&1&0&1\\1&2&1&0\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d266d4b2ade6510fbad4abb393cb493fda356ea0)









![{\displaystyle M=\left[{\begin{matrix}1&0&0&1&0&0\\1&1&0&0&1&1\\0&1&1&0&0&0\\0&0&1&1&1&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b4ecc72d72fdd1b6675d40a696b3d92d3b89938)

