Układ współrzędnych sferycznych
Sferyczny układ współrzędnych – układ współrzędnych w trójwymiarowej przestrzeni euklidesowej.
Istnieje kilka systemów współrzędnych w przestrzeni trójwymiarowej które mogą być uważane za naturalne rozszerzenie układu biegunowego na płaszczyźnie na przestrzeń trójwymiarową. Do takich systemów zalicza się układ współrzędnych walcowych oraz dwa układy współrzędnych sferycznych, roboczo tu nazwanych „matematycznym” oraz „geograficznym”.
W obydwu tych układach istnieją współrzędne odpowiadające odległości od środka pewnej sfery i znanej z geografii długości geograficznej. Różnią się jednak trzecią współrzędną. W systemie „geograficznym” jest ona mierzona od równika (szerokość geograficzna). W systemie „matematycznym” jest ona liczona od bieguna.
W matematycznej literaturze polskojęzycznej występują obydwa typy współrzędnych sferycznych. Na przykład typ „geograficzny” jest przedstawiony w książkach Lei[1] oraz Encyklopedii szkolnej[2], a typ „matematyczny” jest wprowadzany przez Borsuka[3], Starka[4] czy Bronsztejna i Siemiendiajewa[5]. W geografii (współrzędne geograficzne) i astronomii (współrzędne astronomiczne) używa się zawsze współrzędnych opisanych poniżej jako „geograficzne”.
Rys historyczny[edytuj | edytuj kod]
Sferyczny system współrzędnych został przedstawiony i rozwinięty w literaturze matematycznej dużo później niż system biegunowy na płaszczyźnie. Zwyczajowo matematycy uznają, iż system ten był wprowadzony przez Jeana Baptista Clairauta, ale Julian Coolidge[6] ocenia jego wkład jako nieistotny.
Leonhard Euler używał tego systemu w 1748[7], a w 1771[8] podał wzory na przejście do kartezjańskiego układu współrzędnych. Podobnego systemu (i oznaczeń) użył Joseph Louis Lagrange w 1773[9].
System „geograficzny”[edytuj | edytuj kod]
Współrzędne[edytuj | edytuj kod]

Dowolnemu punktowi P przypisujemy jego współrzędne sferyczne:
- promień wodzący czyli odległość punktu P od początku układu O
- długość geograficzną czyli miarę kąta między rzutem prostokątnym wektora na płaszczyznę OXY a osią OX
- szerokość geograficzną czyli miarę kąta między wektorem a jego rzutem na płaszczyznę OXY. Przyjmujemy, że miara kąta jest dodatnia, jeśli rzut wektora na oś OZ jest z nią zorientowany zgodnie i ujemna, gdy rzut ten jest zorientowany przeciwnie do osi.
Dla uniknięcia wieloznaczności przyjmuje się, że dla punktów znajdujących się na osi OZ kąt ma miarę 0 i podobnie, wszystkie współrzędne sferyczne punktu 0 są równe 0.
Przejście do układu kartezjańskiego[edytuj | edytuj kod]
Konwersję z układu sferycznego na współrzędne kartezjańskie punktu P określają wzory:
Jakobian przejścia wynosi
Konwersję z układu kartezjańskiego na sferyczny zadają wzory:
System „matematyczny”[edytuj | edytuj kod]
Współrzędne[edytuj | edytuj kod]

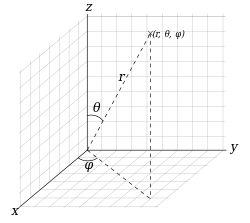
Dowolnemu punktowi M przypisujemy jego współrzędne sferyczne:
- promień wodzący czyli odległość punktu M od początku układu O,
- długość azymutalna (Bronsztejn podaje ), czyli miarę kąta między rzutem prostokątnym wektora na płaszczyznę OXY a dodatnią półosią OX.
- odległość zenitalna czyli miarę kąta między wektorem a dodatnią półosią OZ,
Dla uniknięcia wieloznaczności przyjmuje się, że dla punktów znajdujących się na osi OZ kąt ma miarę 0 i podobnie, wszystkie współrzędne sferyczne punktu O są równe 0.
Przejście do układu kartezjańskiego[edytuj | edytuj kod]
Konwersję z układu sferycznego na współrzędne kartezjańskie punktu M określają wzory:
Jakobian przejścia wynosi
Konwersja z układu kartezjańskiego na sferyczny jest zadana przez:
(Funkcja powinna być tak dobrana, aby wynik był w odpowiedniej ćwiartce ).
Oznaczenia współrzędnych[edytuj | edytuj kod]
Nie jest ustalony jeden system oznaczeń współrzędnych. Przykłady różnych podejść (według MathWorld[10]) podane są poniżej (kolejno promień wodzący, długość azymutalna i odległość zenitalna):
- – Bronsztejn, Siemiediajew 1965, s. 280,
- – Korn and Korn, 1968, s. 60,
- – Misner et al. 1973, s. 205,
- – Arfken 1985, s. 102,
- – Zwillinger 1985, s. 297–298,
- – Beyer 1987, s. 212,
- – Moon and Spencer 1988, s. 24,
- – MathWorld 2005.
Układ sferyczny w astronomii[edytuj | edytuj kod]
W astronomii układ sferyczny to umowny sposób, w jaki podaje się współrzędne na sferze niebieskiej lub na powierzchni kuli ziemskiej. Można tego dokonać wybierając koło główne oraz główne kierunki na tym kole. W takim wypadku jedna ze współrzędnych to kąt między płaszczyzną koła głównego a kierunkiem do określonego punktu należącego do powierzchni kuli, druga natomiast stanowi kąt dwuścienny pomiędzy półpłaszczyznami prostopadłymi do płaszczyzny koła głównego, z których jedna ustawiona jest w kierunku głównym, druga przechodzi przez określony punkt.
Współrzędne hipersferyczne[edytuj | edytuj kod]
Analogicznie do współrzędnych sferycznych w euklidesowej przestrzeni trójwymiarowej definiuje się system współrzędnych hipersferycznych dla dowolnej przestrzeni euklidesowej -wymiarowej, w których składowymi są
- promień wodzący czyli odległość punktu M od początku układu O,
- współrzędnych kątowych gdzie:
- zawierają się w przedziałach
- zawiera się w przedziale
Przejście do układu kartezjańskiego[edytuj | edytuj kod]
Jeśli przez oznaczy się współrzędne kartezjańskie punktu , to można je wyznaczyć w zależności od współrzędnych hipersferycznych wg wzorów[11]
Przejście do układu hipersferycznego[edytuj | edytuj kod]
Konwersję z układu współrzędnych kartezjańskich na współrzędne hipersferyczne punktu określają wzory[11]
Jeżeli dla pewnego a pozostałe współrzędne kartezjańskie są równe zeru, to gdy oraz gdy
Wzory te są jednoznaczne, poza szczególnymi przypadkami: wszystkie współrzędne będą niejednoznacznie określone, gdy wszystkie współrzędne kartezjańskie będą równe zeru; wtedy można wybrać .
Zobacz też[edytuj | edytuj kod]
Inne układy współrzędnych
Szczególne układy współrzędnych
Inne
Przypisy[edytuj | edytuj kod]
- ↑ Franciszek Leja: Geometria analityczna. Wydanie 6. Państw. Wyd. Naukowe, Warszawa 1976, s. 45.
- ↑ Encyklopedia szkolna – Matematyka, Wydawnictwa Szkolne i Pedagogiczne, Warszawa 1990, s. 299, ISBN 83-02-02551-8.
- ↑ Karol Borsuk: Geometria analityczna wielowymiarowa. „Biblioteka Matematyczna”, tom 23, wydanie 2. Państw. Wyd. Naukowe, Warszawa 1964, s. 17.
- ↑ Marceli Stark: Geometria analityczna. „Monografie Matematyczne”, tom 26. Warszawa-Wrocław 1951, s. 68. Plik pdf z Rozdziałem 2.
- ↑ Igor N. Bronsztejn, Konstantin A. Siemiendiajew: Matematyka. Poradnik encyklopedyczny, Państwowe Wydawnictwo Naukowe, Warszawa 1976, s. 280.
- ↑ Julian Coolidge: The Origin of Polar Coordinates. „The American Mathematical Monthly” 59 (1952); s. 83: this apparently is for what he might have done, not what he actually accomplished which seems to have been nothing at all.
- ↑ Euler, Leonhard: Introductio in Analysin infinitorum, tom II, 1748.
- ↑ Leonhard Euler: De solidis quorum superficies in planum explicare licet. „Novi Commentarii Petropolitanae”, 16, 1771, s. 11.
- ↑ Lagrange, Joseph Louis: Sur l’attraction des spheroides elliptiques. „Memoires de l’Academie de Berlin” 1773.
- ↑ Eric W. Weisstein, Spherical Coordinates, [w:] MathWorld, Wolfram Research [dostęp 2020-12-12] (ang.).
- ↑ a b Blumenson, L. E.. A Derivation of n-Dimensional Spherical Coordinates. „The American Mathematical Monthly”, s. 63–66, 1960. DOI: 10.2307/2308932. JSTOR: 2308932.




































![{\displaystyle [0,\pi ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0605c24bcdbdd6ec1817c257b6fb205b62d18d6)










![{\displaystyle {\begin{aligned}r&={\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}+\cdots +{x_{2}}^{2}+{x_{1}}^{2}}}\\[6pt]\varphi _{1}&=\operatorname {arcctg} {\frac {x_{1}}{\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}+\cdots +{x_{2}}^{2}}}}&&=\arccos {\frac {x_{1}}{\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}+\cdots +{x_{1}}^{2}}}}\\[6pt]\varphi _{2}&=\operatorname {arcctg} {\frac {x_{2}}{\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}+\cdots +{x_{3}}^{2}}}}&&=\arccos {\frac {x_{2}}{\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}+\cdots +{x_{2}}^{2}}}}\\[6pt]&\,\,\,\vdots &&\,\,\,\vdots \\[6pt]\varphi _{n-2}&=\operatorname {arcctg} {\frac {x_{n-2}}{\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}}}}&&=\arccos {\frac {x_{n-2}}{\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}+{x_{n-2}}^{2}}}}\\[6pt]\varphi _{n-1}&=2\operatorname {arcctg} {\frac {x_{n-1}+{\sqrt {x_{n}^{2}+x_{n-1}^{2}}}}{x_{n}}}&&={\begin{cases}\arccos {\frac {x_{n-1}}{\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}}}}&x_{n}\geq 0,\\[6pt]2\pi -\arccos {\frac {x_{n-1}}{\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}}}}&x_{n}<0.\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbe2141f7088601da670bef20f515ea4fb79c6ec)






