Powierzchnia Riemanna
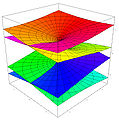
Powierzchnia Riemanna – rozmaitość dwuwymiarowa, która lokalnie wygląda jak płaszczyzna zespolona; jednowymiarowa rozmaitość zespolona. Inaczej mówiąc, na powierzchnie Riemanna można patrzeć jak na rodziny otwartych podzbiorów płaszczyzny zespolonej sklejonych ze sobą poprzez funkcje holomorficzne. Powierzchniami Riemanna po raz pierwszy zajmował się niemiecki matematyk Bernhard Riemann; od niego wzięły swoją nazwę.
Dwuwymiarowa rzeczywista rozmaitość może zostać przekształcona w powierzchnię Riemanna (zazwyczaj na kilka nierównoważnych sposobów) wtedy i tylko wtedy, gdy jest orientowalna. Wynika stąd, że sfera i torus dopuszczają struktury zespolone, natomiast wstęga Möbiusa i butelka Kleina – nie.
Wprowadzenie pojęć[edytuj | edytuj kod]
- Dwuwymiarową rozmaitość topologiczną nazywamy powierzchnią.
- Niech będzie powierzchnią spójną. Rodzinę nazywamy atlasem (zespolonym) powierzchni gdy
- zbiory są otwartymi podzbiorami
- odwzorowania są homeomorfizmami (na swój obraz)
- jeśli są takie, że to odwzorowanie zdefiniowane poniżej jest funkcją holomorficzną
- Jeśli jest atlasem zespolonym, to funkcje nazywamy lokalnymi współrzędnymi (powierzchni) natomiast, pary nazywamy natomiast lokalnymi ścieżkami.
- Dwa atlasy i nazywamy równoważnymi, gdy zbiór jest atlasem. Jest to relacja równoważności w rodzinie atlasów powierzchni Rodzinę klas abstrakcji tej relacji nazywamy strukturą zespoloną powierzchni
- Powierzchnią Riemanna nazywamy spójną powierzchnię wyposażoną w strukturę zespoloną.
Definicje[edytuj | edytuj kod]
Istnieje kilka równoważnych definicji powierzchni Riemanna.
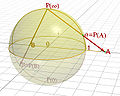
- Powierzchnia Riemanna to rozmaitość zespolona wymiaru zespolonego 1. Oznacza to, że jest hausdorffowską przestrzenią topologiczną wraz z atlasem (zbiorem map pokrywających rozmaitość topologiczną): dla każdego punktu istnieje otoczenie zawierające homeomorficzne z kołem jednostkowym na płaszczyźnie zespolonej. Przekształcenie odwzorowujące strukturę płaszczyzny zespolonej na powierzchnię Riemanna jest nazywane mapą. Dodatkowo homeomorfizmy między dwoma nakładającymi się mapami (tzn. mającymi niepuste przecięcie obrazów) mają być holomorficzne.
- Powierzchnia Riemanna to rozmaitość (rzeczywistego) wymiaru 2 – powierzchnia – wraz ze strukturą konforemną (wiernokątną). Ponownie rozmaitość oznacza, że lokalnie, w dowolnym punkcie przestrzeń ma mieć własności płaszczyzny rzeczywistej. Dodatek „Riemanna” podkreśla, że jest wyposażona w dodatkową strukturę umożliwiającą mierzenie kątów na rozmaitości, dokładniej: klasę równoważności tzw. metryk riemannowskich. Dwie takie metryki uważane są za równoważne, jeżeli kąty, które mierzą, są równe. Wybranie klasy równoważności metryk na to dodatkowa informacja o strukturze konforemnej.
Przejście od struktury zespolonej do struktury konforemnej możliwe jest poprzez wybranie standardowej metryki euklidesowej danej na płaszczyźnie zespolonej i przeniesienie jej na za pomocą map. Pokazanie, że struktura konforemna określa strukturę zespoloną jest trudniejsze.
Przykłady[edytuj | edytuj kod]
Każdy otwarty podzbiór powierzchni Riemanna będący powierzchnią sam jest również powierzchnią Riemanna.
Bibliografia[edytuj | edytuj kod]
- Hershel M. Farkas, Irwin Kra: Riemann Surfaces. Wyd. 2nd. Berlin, New York: Springer-Verlag, 1980. ISBN 978-0-387-90465-8.
- Pablo Arés Gastesi, Riemann Surfaces Book.
- Robin Hartshorne: Algebraic Geometry. Berlin, New York: Springer-Verlag, 1977. MR0463157. ISBN 978-0-387-90244-9. OCLC 13348052., esp. chapter IV.
- Jürgen Jost: Compact Riemann Surfaces. Berlin, New York: Springer-Verlag, 2006, s. 208–219. ISBN 978-3-540-33065-3.
- Carl Ludwig Siegel. Meromorphe Funktionen auf kompakten analytischen Mannigfaltigkeiten. „Nachrichten der Akademie der Wissenschaften in Göttingen. II. Mathematisch-Physikalische Klasse”, s. 71–77, 1955. ISSN 0065-5295. MR0074061.
- Hermann Weyl: The Concept of a Riemann Surface. Addison-Wesley, 1964.