Graf krawędziowy
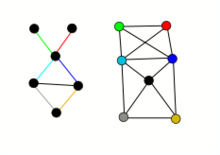
Graf krawędziowy (ang. line graph) grafu G – taki graf F=L(G), którego zbiorem wierzchołków jest zbiór krawędzi grafu G: V(F) = E(G), natomiast zbiorem krawędzi E(F) jest zbiór par elementów zbioru E(G), przy czym:
- Wierzchołki {v1, v2}, {v3, v4} grafu F są połączone wtedy i tylko wtedy, gdy v1=v3 lub v1=v4 lub v2=v3 lub v2=v4.
- Od wierzchołka (v1, v2) do wierzchołka (v3, v4) grafu F prowadzi krawędź wtedy i tylko wtedy, gdy v2=v3.
Intuicyjnie można to rozumieć tak, że krawędzie grafu G traktujemy jako wierzchołki, tworząc graf F, a wierzchołki grafu F łączymy krawędziami wtedy, gdy „istnieje przejście” pomiędzy krawędziami grafu G odpowiadającym odpowiednim wierzchołkom grafu F.
Jeśli nie powiedziano inaczej, pojęcie grafu krawędziowego odnosi się tylko do grafów nieskierowanych.
Interesującym zagadnieniem jest pytanie, czy dany graf jest grafem krawędziowym jakiegoś grafu, oraz czy każdy graf jest grafem krawędziowym jakiegoś grafu.
Lowell W. Beineke w 1968 r. pokazał, że graf jest grafem krawędziowym jakiegoś grafu wtedy i tylko wtedy, gdy nie zawiera żadnego z dziewięciu wymienionych grafów:

- Graf krawędziowy grafu spójnego jest grafem spójnym.
- indeks chromatyczny grafu jest równy liczbie chromatycznej jego grafu krawędziowego[1].
Przypisy[edytuj | edytuj kod]
- ↑ Reinhard Diestel: Graph Theory. Nowy Jork: 2000, s. 96. ISBN 0-387-95014-1.


