Kula

Definicja intuicyjna

Kula to zbiór punktów oddalonych nie bardziej niż pewna zadana odległość (promień kuli) od wybranego punktu (środek kuli).

Kula – uogólnienie pojęcia koła na więcej wymiarów, zdefiniowane dla wszystkich przestrzeni metrycznych.

Definicja formalna

Kula w danej przestrzeni metrycznej $(X,\rho )$ – zbiór elementów tej przestrzeni, zdefiniowany jako:

${\overline {K}}_{c,r}=\{p:\rho (p,c)\leqslant r\}$

dla pewnych $c\in X,\ r>0,$ które nazywamy odpowiednio środkiem i promieniem kuli.

W wielu źródłach tak zdefiniowany zbiór nazywany jest kulą domkniętą dla odróżnienia od zbioru określanego jako kula otwarta (inaczej kula bez brzegu) i definiowanego następująco:

$K_{c,r}=\{p:\rho (p,c)<r\}.$

Informacja ogólna

Kula w przestrzeni euklidesowej

Kula o środku $P(2;1{,}5)$ i promieniu $r=1$ w metryce Manhattan na zbiorze $\mathbb {R} ^{2}.$

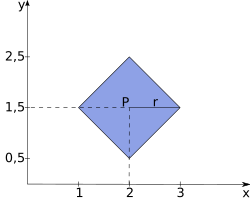
Intuicyjnie rozumiana kula – w przestrzeni euklidesowej trójwymiarowej dla metryki euklidesowej – jest to część przestrzeni, ograniczona sferą (sfera jest powierzchnią (brzegiem) kuli i również się w niej zawiera).

Taką kulę można wówczas opisać wzorem jako zbiór punktów, których współrzędne $(x,y,z)$ spełniają nierówność:

$(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}\leqslant r^{2},$

gdzie $(x_{0},y_{0},z_{0})$ są współrzędnymi środka kuli, a $r$ oznacza jej promień, natomiast w układzie współrzędnych sferycznych, dla środka znajdującego się w środku układu współrzędnych:

$r(\alpha ,\beta )\leqslant r\;{}$ dla ${}\,\alpha \in [-\pi ,\pi ),\beta \in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right].$

W $n$-wymiarowej przestrzeni euklidesowej wzór ten ma natychmiastowe uogólnienie – kula o środku w punkcie $(s_{1},s_{2},\dots ,s_{n})$ i promieniu $r$ to zbiór punktów $x=(x_{1},x_{2},\dots ,x_{n}),$ których współrzędne spełniają nierówność:

$(x_{1}-s_{1})^{2}+(x_{2}-s_{2})^{2}+\ldots +(x_{n}-s_{n})^{2}\leqslant r^{2}.$

Nietrudno zauważyć, że w dwuwymiarowej przestrzeni euklidesowej kulą jest koło, zaś w jednowymiarowej – odcinek.

Dla innych metryk kula wyglądać będzie inaczej. Przykładowo, w przestrzeni $\mathbb {R} ^{2}$ o metryce Manhattan do kuli należą punkty, spełniające nierówność:

$\left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right|\leqslant r.$

Natomiast w przestrzeni liter alfabetu łacińskiego, gdzie metryką byłaby odległość między poszczególnymi literami w szyku alfabetu, kulą jest np. zbiór $\{G,H,I\}$ – promień tej kuli wynosi 1, a jej środkiem jest $H.$

Związane pojęcia

Cięciwa kuli to odcinek o końcach na brzegu kuli.

Średnica kuli to cięciwa przechodząca przez środek kuli. Termin ten oznacza również długość tej cięciwy – równą podwojonej długości promienia kuli. Termin ten został uogólniony na wszelkie zbiory w przestrzeni metrycznej (zobacz średnica zbioru).

Koło wielkie kuli to koło o promieniu tej kuli, o środku w środku kuli.

Wzory dla kuli w przestrzeni euklidesowej

• Objętość $n$-wymiarowej kuli (hiperkuli) o promieniu $r$ dana jest wzorem $V_{n}={\frac {\pi ^{\frac {n}{2}}}{\Gamma ({\frac {n}{2}}+1)}}\cdot r^{n}={\begin{cases}\displaystyle {\frac {\pi ^{k}}{k!}}\cdot r^{n}&{\text{dla }}n=2k,\\[2ex]\displaystyle {\frac {2^{k}\pi ^{k-1}}{n!!}}\cdot r^{n}&{\text{dla }}n=2k-1,\end{cases}}$

• „Pole” $(n-1)$-wymiarowe jej (hiper)powierzchni $S_{n}={\frac {n}{r}}\,V_{n}.$
• Objętość 3-wymiarowej kuli: $V={\frac {4}{3}}\pi r^{3}\approx 4{,}19\ r^{3}.$
• Pole powierzchni 3-wymiarowej kuli: $S=4\pi r^{2}\approx 12{,}6\ r^{2}.$

W powyższych wzorach $\pi \approx 3{,}14159265$ jest jedną z najsłynniejszych stałych matematycznych, szerzej opisaną w artykule Pi, zaś $\Gamma$ oznacza funkcję gamma.

Uwaga: Brzegiem $n$-wymiarowej kuli jest $(n-1)$-wymiarowa sfera.

Uogólnienie topologiczne

W topologii kulę definiujemy jako rozmaitość topologiczną, homeomorficzną z kulą geometryczną, zdefiniowaną jak powyżej.

Zobacz też

• czasza kuli (odcinek kuli)
• hiperkula
• sfera
• warstwa kulista
• wycinek kuli
• kula ziemska