Przestrzeń styczna

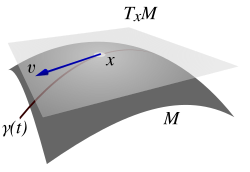
Przestrzeń styczna $T_{x}M$ 2-wymiarowa (płaszczyzna) do 2-wymiarowej rozmaitości $M$ (powierzchni) w punkcie $x$ oraz wektor styczny $v\in T_{x}M$ do krzywej $\gamma$ przechodzącej przez punkt $x\in M.$

Przestrzeń styczna – to przestrzeń liniowa utworzona z wektorów zaczepionych w ustalonym punkcie $x$ przestrzeni $M,$ przy czym:

1. Przestrzeń $M$ w ogólności może być dowolną rozmaitością topologiczną.
2. Wymiar przestrzeni stycznej jest równy wymiarowi rozmaitości $M.$
3. Każdy element przestrzeni stycznej – wektor styczny do $M$ w punkcie $x$ – jest styczny do jakiejś krzywej gładkiej rozmaitości, przechodzącej przez punkt $x.$
4. Przestrzeń styczną do $M$ w punkcie $x$ oznacza się $T_{x}(M)$ lub $T_{x}M.$

Przestrzenie styczne do rozmaitości w różnych jej punktach są różnymi przestrzeniami.

Wektory z przestrzeni stycznej tworzą zbiór możliwych wektorów prędkości $v,$ jakie może mieć ciało w położeniu $x,$ poruszając się po rozmaitości. Po przesunięciu się ciała do innego punktu prędkość ciała będzie dana przez inny wektor – taki, który należy do przestrzeni stycznej tego punktu (nie jest to widoczne na rysunku).

Przestrzeń styczna do 2-wymiarowej powierzchni

Przestrzeń styczna (płaszczyzna styczna) w punkcie $x$ na sferze.

Wszystkie krzywe przechodzące przez dany punkt $x$ leżący na 2-wymiarowej powierzchni $M$ (np. powierzchni sfery czy elipsoidy itp.) mają wektor styczny, zaczepiony w tym punkcie. Suma dwóch wektorów stycznych jest nadal wektorem stycznym do jakiejś krzywej na tej powierzchni, przechodzącej przez punkt $x.$ To samo dotyczy mnożenia wektorów stycznych przez skalar.

Wszystkie wektory styczne do krzywych na powierzchni rozpinają więc w punkcie $x$ 2-wymiarową przestrzeń styczną – płaszczyznę styczną w punkcie $x$ do powierzchni $M.$

Płaszczyzna styczna w punkcie $x$ stanowi więc przybliżenie płaskie (liniowe w 2 wymiarach) powierzchni zakrzywionej $M;$ przybliżenie to jest tym lepsze, im bliżej punktu $x$ znajdują się punkty rozmaitości.

Przestrzeń styczna do 3-wymiarowej przestrzeni euklidesowej

W 3-wymiarowej przestrzeni euklidesowej $E$ wektor zaczepiony w pewnym punkcie jest określony przez punkt zaczepienia oraz 3 współrzędne. Wektory zaczepione w różnych punktach uważa się za odrębne, nawet jeśli mają te same współrzędne. Wektory zaczepione w tym samym punkcie $x$ tworzą 3-wymiarową przestrzeń euklidesową, gdyż spośród wszystkich takich wektorów można wybrać tylko 3 liniowo niezależne. Wektory te tworzą bazę przestrzeni stycznej do $E$ w punkcie $x$ i oznacza symbolem $T_{x}(E).$

Wektory należą do tej samej przestrzeni stycznej, jeżeli mają ten sam punkt zaczepienia. Wektory zaczepione w różnych punktach przestrzeni $E$ należą do różnych przestrzeni stycznych.

Przestrzeń styczna do 3-wymiarowej rozmaitości

Krzywe w 3-wymiarowej, dowolnej rozmaitości $M$ przechodzące przez ustalony punkt $x$ mają wektory do nich styczne w tym punkcie. Wektory te rozpinają 3-wymiarową przestrzeń euklidesową, styczną do przestrzeni $M$ w punkcie $x,$ która jest aproksymacją płaską rozmaitości w ogólnym przypadku dowolnie zakrzywionej.

Przestrzeń styczna – pojęcie wewnętrzne rozmaitości

W opisie przestrzeni stycznej do dowolnej rozmaitości nie jest konieczne odwoływanie się do przestrzeni euklidesowej wyższego wymiaru, w której ta rozmaitość jest zanurzona.

Przykładowo sfera jest rozmaitością różniczkową 2-wymiarową. Powierzchnię sfery w otoczeniu punktu $x$ można sparametryzować za pomocą współrzędnych sferycznych $\theta$ i $\phi .$ Mówi się, że za pomocą tych współrzędnych określona jest mapa ze sfery na przestrzeń $\mathbb {R} ^{2},$ przy czym:

• każdemu punktowi $x$ na sferze odpowiada jednoznacznie punkt o współrzędnych $(\theta (x),\phi (x))$ w przestrzeni $\mathbb {R} ^{2};$
• każdej krzywej $x(t)$ na sferze odpowiada jednoznacznie krzywa w $\mathbb {R} ^{2}$ złożona z punktów o współrzędnych $(\theta (t),\phi (t))$ odpowiadających punktom $x(t)$ krzywej;
• wektorowi stycznemu do krzywej na sferze odpowiada wektor styczny do krzywej w przestrzeni $\mathbb {R} ^{2}.$

Tak określona przestrzeń styczna jest przestrzenią wektorową wymiaru 2, czyli tego samego wymiaru co sfera, do której jest styczna, gdyż:

• działaniom dodawania wektorów na sferze i mnożenia ich przez skalar (czyli działania określone w każdej przestrzeni wektorowej) odpowiadają analogiczne działania na odpowiadających im wektorach w przestrzeni $\mathbb {R} ^{2};$
• przestrzeń styczna nie zależy od wyboru współrzędnych krzywoliniowych i będzie identyczna dla każdej innej mapy.

Zatem wektory styczne do sfery w punkcie $x$ tworzą 2-wymiarową przestrzeń styczną – płaszczyznę $\mathbb {R} ^{2}.$ Pokazaliśmy to nie odwołując się do pojęcia zanurzenia sfery w przestrzeni 3-wymiarowej.

Przestrzeń styczna do n-wymiarowej rozmaitości

Rozmaitość w najogólniejszym przypadku jest przestrzenią topologiczna, która ma lokalnie własności przestrzeni euklidesowej. Rozmaitość ma wymiar $n,$ jeżeli przez każdy punkt $x$ rozmaitości przechodzą krzywe, których wektory styczne tworzą n-wymiarowe przestrzenie styczne (przestrzenie euklidesowe).

Definicja formalna przestrzeni stycznej

(1) Niech $(U,\phi )$ będzie mapą otoczenia $U$ punktu $x$ rozmaitości różniczkowej $M$ klasy $C^{1}$ wymiaru $n.$

Krzywą klasy $C^{r}$ na rozmaitości $M$ przechodzącą przez punkt $x$ nazywa się odwzorowanie $\gamma$ klasy $C^{r}$ dowolnego przedziału $(-\epsilon ,\epsilon )\subset \mathbb {R}$ w $M,$ tj.

$\gamma :\ (-\epsilon ,\epsilon )\to M,$

takie że $\gamma (0)=x.$

(2) Na zbiorze ${\overline {T}}_{p}(M)$ wszystkich krzywych klasy $C^{1}$ na rozmaitości $M$ i przechodzących przez punkt $x$ określamy relację równoważności $\sim$ taką, że dwie krzywe $\gamma _{1}$ i $\gamma _{2}$ są w relacji o ile wektory styczne w zerze do krzywych $\phi \circ \gamma _{1}$ oraz $\phi \circ \gamma _{2}$ (obie krzywe leżą w $\mathbb {R} ^{n}$) są równe, czyli:

$\gamma _{1}\sim \gamma _{2}\iff {\frac {\mathrm {d} }{\mathrm {d} t}}(\phi \circ \gamma _{1}){\Big |}_{t=0}={\frac {\mathrm {d} }{\mathrm {d} t}}(\phi \circ \gamma _{2}){\Big |}_{t=0}$

Można sprawdzić, że taka definicja relacji nie zależy od wyboru początkowej mapy $(U,\phi ).$

(3) Przestrzeń styczną do rozmaitości różniczkowej $M$ klasy $C^{1}$ w punkcie $x,$ oznaczaną $T_{x}(M),$ definiuje się jako zbiór klas abstrakcji relacji $\sim {:}$

$T_{x}(M):={\overline {T}}_{x}(M)/\sim$

Odwzorowanie ${\overline {\Theta }}_{\phi }:{\overline {T}}_{x}(M)\to \mathbb {R} ^{n}$ przyporządkowujące krzywej $\gamma ,$ przechodzącej przez $x,$ jej wektor styczny w zerze:

${\overline {\Theta }}_{\phi }(\gamma ):={\frac {\mathrm {d} }{\mathrm {d} t}}(\phi \circ \gamma ){\Big |}_{t=0}$

jest stałe na klasach abstrakcji relacji $\sim$ i indukuje bijekcję $\Theta _{\phi }:\ T_{x}(M)\to \mathbb {R} ^{n},$ daną wzorem: $\Theta _{\phi }(\gamma '):={\frac {\mathrm {d} }{\mathrm {d} t}}(\phi \circ \gamma ){\Big |}_{t=0},$ gdzie $\gamma '$ oznacza klasę abstrakcji krzywej $\gamma$ względem relacji $\sim$ $(\gamma '\in T_{x}(M)).$ Zatem $T_{x}(M)$ ma strukturę przestrzeni liniowej wymiaru $n,$ przeniesioną przez bijekcję $\Theta _{\phi },$ tzn. działania w przestrzeni stycznej $T_{x}(M)$ definiujemy następująco:

$u+v:=\Theta _{\phi }^{-1}(\Theta _{\phi }(u)+\Theta _{\phi }(v)),$ dla dowolnych $u,\ v\in T_{x}(M),$

$\alpha \cdot v:=\Theta _{\phi }^{-1}(\alpha \Theta _{\phi }(v)),$ dla dowolnego $v\in T_{x}(M),$ oraz dowolnego $\alpha \in \mathbb {R} .$

(4) Niezależność od wyboru mapy

Definicja przestrzeni stycznej nie zależy od wyboru mapy początkowej $(U,\phi ).$ Wzięcie innej mapy nie zmienia równości wektorów stycznych do krzywych, czyli relacji $\sim .$

Zobacz też

• przestrzeń kostyczna
• wektor styczny
• wiązka styczna
• współrzędne krzywoliniowe

Bibliografia

• WojciechW. Wojtyński WojciechW., Grupy i algebry Liego, Warszawa: PWN, 1986, ISBN 83-01-04934-0, OCLC 835897238 .brak strony (książka)