Wikiprojekt:Tłumaczenie artykułów/1 − 2 + 3 − 4 + · · ·

Kilka pierwszych tysięcy wyrazów sum częściowych szeregu 1 − 2 + 3 − 4 + …

1 − 2 + 3 − 4 + · · · w matematyce jest to nieskończony szereg, którego wyrazami są kolejne liczby całkowite dodatnie, wzięte z przemiennym znakiem. Zapisując standardowo sumowanie z użyciem wielkiej litery sigma możemy szereg wyrazić jako:

$\sum _{n=1}^{m}n(-1)^{n-1}.$

Szereg ten jest rozbieżny, tzn. ciąg jego sum częściowych (1, −1, 2, −2, …) nie dąży do żadnej skończonej granicy. Równoważnie mówimy, że szereg 1 − 2 + 3 − 4 + … nie ma sumy.

Mimo to, w połowie 18 wieku Leonhard Euler napisał równanie, które sam nazwał paradoksalnym:

$1-2+3-4+\cdots ={\frac {1}{4}}.$

Ścisłe objaśnienie tego równania pojawiło się jednak znacznie później. Dopiero po 1890 roku Ernesto Cesàro, Émile Borel i inni badali ściśle określone metody przypisywania uogólnionych sum szeregom rozbieżnym – w tym obejmujące nowe interpretacje prób Eulera. Mimo wszystko wiele tych metod łatwo przypisuje szeregowi 1 − 2 + 3 − 4 + … "sumę" ${\tfrac {1}{4}}$. en:Cesàro summation jest jedną z kilku metod, które nie definiują sumy dla szeregu 1 − 2 + 3 − 4 + … tak, że szereg jest przykładem wymagającym metody nieco silniejszej, takiej jak suma en:Abel summation.

Szereg 1 − 2 + 3 − 4 + … jest blisko związany z szeregiem Grandiego 1 − 1 + 1 − 1 + …. Euler omawiał je jako specjalne przypadki 1 − 2ⁿ + 3ⁿ − 4ⁿ + … dla dowolnego n. Ten kierunek badań rozszerzył jego prace na problem bazylejski, wiodąc ku równaniom funkcyjnym, których rozwiązania dziś znane są jako funkcja "eta" Dirichleta oraz funkcja "dzeta" Riemanna.

Rozbieżność

Kolejne wyrazy ciągu (1, −2, 3, −4, …) nie zbliżają się do zera; stąd, na mocy twierdzenia przeciwstawnego do warunku koniecznego zbieżności szeregu, szereg 1 − 2 + 3 − 4 + … jest rozbieżny. Dla dalszego wywodu przyda się wyjaśnić tę rozbieżność w sposób bardziej podstawowy. Z definicji zbieżność albo rozbieżność szeregu wynika ze zbieżności albo rozbieżności ciągu jego sum częściowych, zaś ciągiem sum częściowych szeregu 1 − 2 + 3 − 4 + … jest:

1 = 1,

1 − 2 = −1,

1 − 2 + 3 = 2,

1 − 2 + 3 − 4 = −2,

1 − 2 + 3 − 4 + 5 = 3,

1 − 2 + 3 − 4 + 5 − 6 = −3,

…

Ciąg ten ma za wyrazy wszystkie liczby całkowite (również 0, jeśli uwzględnić sumę pustą – por. Dodawanie#Zapis oraz liczba składników), ustala więc przeliczalność zbioru $\mathbb {Z}$ liczb całkowitych. Ciąg sum częściowych wyraźnie pokazuje, że szereg nie jest zbieżny do żadnej konkretnej liczby (dla każdej zaproponowanej granicy x, można wskazać punkt, poza którym kolejne częściowe sumy są poza przedziałem [x-1, x+1]), a więc 1 − 2 + 3 − 4 + … jest rozbieżny.

Heuristics for summation

Stabilność i liniowość

Ponieważ kolejne wyrazy 1, −2, 3, −4, 5, −6, … tworzą prosty wzór, szereg 1 − 2 + 3 − 4 + … może być manipulowany poprzez przesunięcia i term-by-term addition, aby uzyskać wartość numeryczną. Jeśli ma sens zapisanie s = 1 − 2 + 3 − 4 + … dla pewnej liczby, to następujące manipulacje wykazują, że s = ${\tfrac {1}{4}}$:

${\begin{array}{rclllll}4s&=&&(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )\\&=&&(1-2+3-4+\cdots )&+1+(-2+3-4+5+\cdots )&+1+(-2+3-4+5+\cdots )&-1+(3-4+5-6\cdots )\\&=&1+[&(1-2-2+3)&+(-2+3+3-4)&+(3-4-4+5)&+(-4+5+5-6)+\cdots ]\\&=&1+[&0+0+0+0+\cdots ]\\4s&=&1\end{array}}$

Suma 4 kopii szeregu 1 − 2 + 3 − 4 + …, przy wykorzystaniu tylko przesunięć i term-by-term addition, wynosi 1. Lewa i prawa strona rysunku reprezentują dwie kopie 1 − 2 + 3 − 4 + …, które są upraszczane do równania 1 − 1 + 1 − 1 + ….

Stąd $s={\frac {1}{4}}$. Sposób postępowania został przedstawiony graficznie na rysunku po prawej stronie.

Chociaż 1 − 2 + 3 − 4 + … nie posiada sumy w zwyczajnym znaczeniu, równanie s = 1 − 2 + 3 − 4 + … = ${\tfrac {1}{4}}$ może zostać uznane jako najbardziej naturalne rozwiązanie, jeśli suma miałaby zostać określona. Uogólnioną definicję "sumy" szeregu rozbieżnego nazywa się metodą sumowania, która dodaje pewne podzbiory ze wszystkich możliwych szeregów. Istnieje wiele różnych metod (kilka z nich jest opisanych poniżej), charakteryzowanych na podstawie właściwości, które współdzielą ze zwykłym dodawaniem. Powyższe manipulacje dowodzą tego, że: biorąc pod uwagę metodę sumowania, która jest stabilna i liniowa oraz sumuje szereg 1 − 2 + 3 − 4 + …, otrzymujemy ${\tfrac {1}{4}}$. Dodatkowo, ponieważ:

${\begin{array}{rcllll}2s&=&&(1-2+3-4+\cdots )&+&(1-2+3-4+\cdots )\\&=&1+&(-2+3-4+\cdots )&+1-2&+(3-4+5\cdots )\\&=&0+&(-2+3)+(3-4)+(-4+5)+\cdots \\{\frac {1}{2}}&=&&1-1+1-1\cdots \\\end{array}}$

metoda ta musi również sumować Szereg Grandiego jako 1 − 1 + 1 − 1 + … = ${\tfrac {1}{2}}$.

Cauchy product

In 1891, Ernesto Cesàro expressed hope that divergent series would be rigorously brought into calculus, pointing out, "One already writes (1 − 1 + 1 − 1 + …)² = 1 − 2 + 3 − 4 + … and asserts that both the sides are equal to ${\tfrac {1}{4}}$." For Cesàro, this equation was an application of a theorem he had published the previous year, one that may be identified as the first theorem in the history of summable divergent series. The details on his summation method are below; the central idea is that 1 − 2 + 3 − 4 + … is the Cauchy product of 1 − 1 + 1 − 1 + … with 1 − 1 + 1 − 1 + ….

The Cauchy product of two infinite series is defined even when both of them are divergent. In the case where Σa_n = Σb_n = Σ(−1)ⁿ, the terms of the Cauchy product are given by the finite diagonal sums

${\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{array}}$

The product series is then

$\sum _{n=0}^{\infty }(-1)^{n}(n+1)=1-2+3-4+\cdots .$

Thus a summation method that respects the Cauchy product of two series and sums 1 − 1 + 1 − 1 + … = ${\tfrac {1}{2}}$, will also sum 1 − 2 + 3 − 4 + … = ${\tfrac {1}{4}}$. With the result of the previous section, this implies an equivalence between summability of 1 − 1 + 1 − 1 + … and 1 − 2 + 3 − 4 + … with methods that are linear, stable, and respect the Cauchy product.

Cesàro's theorem is a subtle example. The series 1 − 1 + 1 − 1 + … is Cesàro-summable in the weakest sense, called (C, 1)-summable, while 1 − 2 + 3 − 4 + … requires a stronger form of Cesàro's theorem, being (C, 2)-summable. Since all forms of Cesàro's theorem are linear and stable, the values of the sums are as we have calculated.

Specific methods

Cesàro and Hölder

Data about the (H, 2) sum of ${\tfrac {1}{4}}$

To find the (C, 1) Cesàro sum of 1 − 2 + 3 − 4 + …, if it exists, one needs to compute the arithmetic means of the partial sums of the series. The partial sums are

1, −1, 2, −2, 3, −3, …,

and the arithmetic means of these partial sums are

1, 0, ${\tfrac {2}{3}}$, 0, ${\tfrac {3}{5}}$, 0, ${\tfrac {4}{7}}$, ….

This sequence of means does not converge, so 1 − 2 + 3 − 4 + … is not Cesàro summable.

There are two well-known generalizations of Cesàro summation: the conceptually simpler of these is the sequence of (H, n) methods for natural numbers n. The (H, 1) sum is Cesàro summation, and higher methods repeat the computation of means. Above, the even means converge to ${\tfrac {1}{2}}$, while the odd means are all equal to 0, so the means of the means converge to the average of 0 and ${\tfrac {1}{2}}$, namely ${\tfrac {1}{4}}$. So 1 − 2 + 3 − 4 + … is (H, 2) summable to ${\tfrac {1}{4}}$.

The "H" stands for Otto Hölder, who first proved in 1882 what mathematicians now think of as the connection between Abel summation and (H, n) summation; 1 − 2 + 3 − 4 + … was his first example. The fact that ${\tfrac {1}{4}}$ is the (H, 2) sum of 1 − 2 + 3 − 4 + … guarantees that it is the Abel sum as well; this will also be proved directly below.

The other commonly formulated generalization of Cesàro summation is the sequence of (C, n) methods. It has been proven that (C, n) summation and (H, n) summation always give the same results, but they have different historical backgrounds. In 1887, Cesàro came close to stating the definition of (C, n) summation, but he gave only a few examples. In particular, he summed 1 − 2 + 3 − 4 + …, to ${\tfrac {1}{4}}$ by a method that may be rephrased as (C, n) but was not justified as such at the time. He formally defined the (C, n) methods in 1890 in order to state his theorem that the Cauchy product of a (C, n)-summable series and a (C, m)-summable series is (C, m + n + 1)-summable.

Abel summation

Some partials of 1−2x+3x²+…; 1/(1 + x)²; and limits at 1

In a 1749 report, Leonhard Euler admits that the series diverges but prepares to sum it anyway:

…when it is said that the sum of this series 1−2+3−4+5−6 etc. is ${\tfrac {1}{4}}$, that must appear paradoxical. For by adding 100 terms of this series, we get –50, however, the sum of 101 terms gives +51, which is quite different from ${\tfrac {1}{4}}$ and becomes still greater when one increases the number of terms. But I have already noticed at a previous time, that it is necessary to give to the word sum a more extended meaning….

{{Cytat}} Brakujące pola: treść. Przestarzałe pola: 1.

Euler proposed a generalization of the word "sum" several times; see Euler on infinite series. In the case of 1 − 2 + 3 − 4 + …, his ideas are similar to what is now known as Abel summation:

…it is no more doubtful that the sum of this series 1−2+3−4+5 + etc. is ${\tfrac {1}{4}}$; since it arises from the expansion of the formula ${\tfrac {1}{(1+1)^{2}}}$, whose value is incontestably ${\tfrac {1}{4}}$. The idea becomes clearer by considering the general series 1 − 2x + 3x² − 4x³ + 5x⁴ − 6x⁵ + &c. that arises while expanding the expression ${\tfrac {1}{(1+x)^{2}}}$, which this series is indeed equal to after we set x = 1.

{{Cytat}} Brakujące pola: treść. Przestarzałe pola: 1.

There are many ways to see that, at least for absolute values |x| < 1, Euler is right in that

$1-2x+3x^{2}-4x^{3}+\cdots ={\frac {1}{(1+x)^{2}}}.$

One can take the Taylor expansion of the right-hand side, or apply the formal long division process for polynomials. Starting from the left-hand side, one can follow the general heuristics above and try multiplying by (1+x) twice or squaring the geometric series 1 − x + x² − …. Euler also seems to suggest differentiating the latter series term by term.

In the modern view, the series 1 − 2x + 3x² − 4x³ + … does not define a function at x = 1, so that value cannot simply be substituted into the resulting expression. Since the function is defined for all |x| < 1, one can still take the limit as x approaches 1, and this is the definition of the Abel sum:

$\lim _{x\rightarrow 1^{-}}\sum _{n=1}^{\infty }n(-x)^{n-1}=\lim _{x\rightarrow 1^{-}}{\frac {1}{(1+x)^{2}}}={\frac {1}{4}}.$

Euler and Borel

Euler summation to ${\tfrac {1}{2}}$ − ${\tfrac {1}{4}}$

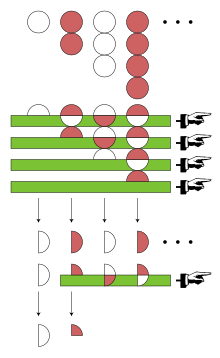
Euler applied another technique to the series: the Euler transform, one of his own inventions. To compute the Euler transform, one begins with the sequence of positive terms that makes up the alternating series—in this case 1, 2, 3, 4, …. The first element of this sequence is labeled a₀.

Next one needs the sequence of forward differences among 1, 2, 3, 4, …; this is just 1, 1, 1, 1, …. The first element of this sequence is labeled Δa₀. The Euler transform also depends on differences of differences, and higher iterations, but all the forward differences among 1, 1, 1, 1, … are 0. The Euler transform of 1 − 2 + 3 − 4 + … is then defined as

${\frac {1}{2}}a_{0}-{\frac {1}{4}}\Delta a_{0}+{\frac {1}{8}}\Delta ^{2}a_{0}-\cdots ={\frac {1}{2}}-{\frac {1}{4}}.$

In modern terminology, one says that 1 − 2 + 3 − 4 + … is Euler summable to ${\tfrac {1}{4}}$.

The Euler summability implies another kind of summability as well. Representing 1 − 2 + 3 − 4 + … as

$\sum _{k=0}^{\infty }a_{k}=\sum _{k=0}^{\infty }(-1)^{k}(k+1),$

one has the related everywhere-convergent series

$a(x)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}(k+1)x^{k}}{k!}}=e^{-x}(1-x).$

The Borel sum of 1 − 2 + 3 − 4 + … is therefore

$\int _{0}^{\infty }e^{-x}a(x)\,dx=\int _{0}^{\infty }e^{-2x}(1-x)\,dx={\frac {1}{2}}-{\frac {1}{4}}.$

Separation of scales

Saichev and Woyczyński arrive at 1 − 2 + 3 − 4 + … = ${\tfrac {1}{4}}$ by applying only two physical principles: infinitesimal relaxation and separation of scales. To be precise, these principles lead them to define a broad family of "φ-summation methods", all of which sum the series to ${\tfrac {1}{4}}$:

• If φ(x) is a function whose first and second derivatives are continuous and integrable over (0, ∞), such that φ(0) = 1 and the limits of φ(x) and xφ(x) at +∞ are both 0, then

$\lim _{\delta \rightarrow 0}\sum _{m=0}^{\infty }(-1)^{m}(m+1)\varphi (\delta m)={\frac {1}{4}}.$

This result generalizes Abel summation, which is recovered by letting φ(x) = exp(-x). The general statement can be proved by pairing up the terms in the series over m and converting the expression into a Riemann integral. For the latter step, the corresponding proof for 1 − 1 + 1 − 1 + … applies the mean value theorem, but here one needs the stronger Lagrange form of Taylor's theorem.

Uogólnienia

Euler sums similar series in the 1755 Institutiones

The threefold Cauchy product of 1 − 1 + 1 − 1 + … is 1 − 3 + 6 − 10 + …, the alternating series of triangular numbers; its Abel and Euler sum is ${\tfrac {1}{8}}$. The fourfold Cauchy product of 1 − 1 + 1 − 1 + … is 1 − 4 + 10 − 20 + …, the alternating series of tetrahedral numbers, whose Abel sum is ${\tfrac {1}{16}}$.

Another generalization of 1 − 2 + 3 − 4 + … in a slightly different direction is the series 1 − 2ⁿ + 3ⁿ − 4ⁿ + … for other values of n. For positive integers n, these series have the following Abel sums:

$1-2^{n}+3^{n}-\cdots ={\frac {2^{n+1}-1}{n+1}}B_{n+1}$

where B_n are the Bernoulli numbers. For even n, this reduces to

$1-2^{2k}+3^{2k}-\cdots =0.$

This last sum became an object of particular ridicule by Niels Henrik Abel in 1826:

"Divergent series are on the whole devil's work, and it is a shame that one dares to found any proof on them. One can get out of them what one wants if one uses them, and it is they which have made so much unhappiness and so many paradoxes. Can one think of anything more appalling than to say that

0 = 1 − 2ⁿ + 3ⁿ − 4ⁿ + etc.

where n is a positive number. Here's something to laugh at, friends."

Cesàro's teacher, Eugène Charles Catalan, also disparaged divergent series. Under Catalan's influence, Cesàro initially referred to the "conventional formulas" for 1 − 2ⁿ + 3ⁿ − 4ⁿ + … as "absurd equalities", and in 1883 Cesàro expressed a typical view of the time that the formulas were false but still somehow formally useful. Finally, in his 1890 Sur la multiplication des séries, Cesàro took a modern approach starting from definitions.

The series are also studied for non-integer values of n; these make up the Dirichlet eta function. Part of Euler's motivation for studying series related to 1 − 2 + 3 − 4 + … was the functional equation of the eta function, which leads directly to the functional equation of the Riemann zeta function. Euler had already become famous for finding the values of these functions at positive even integers (including the Basel problem), and he was attempting to find the values at the positive odd integers (including Apéry's constant) as well, a problem that remains elusive today. The eta function in particular is easier to deal with by Euler's methods because its Dirichlet series is Abel summable everywhere; the zeta function's Dirichlet series is much harder to sum where it diverges. For example, the counterpart of 1 − 2 + 3 − 4 + … in the zeta function is the non-alternating series 1 + 2 + 3 + 4 + …, which has deep applications in modern physics but requires much stronger methods to sum.

Bibliografia

• Richard Beals: Analysis: an introduction. Cambridge UP, 2004. ISBN 0-521-60047-2. (ang.).brak strony w książce
• Harry F. Davis: Fourier Series and Orthogonal Functions. Dover, maj 1989. ISBN 0-486-65973-9. (ang.).brak strony w książce
• Euler, Leonhard; Lucas Willis; and Thomas J Osler: Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series. 2006. [dostęp 2007-03-22]. (ang.).{{Cytuj stronę}} Nieznane pola: "wydawca". Pierwotnie opublikowane jako: Leonhard Euler. Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques. „Memoires de l'academie des sciences de Berlin”, s. 83–106, 1768. (ang.). {{Cytuj pismo}} Nieznane pola: "tom".
• Giovanni Ferraro. The First Modern Definition of the Sum of a Divergent Series: An Aspect of the Rise of 20th Century Mathematics. „Archive for History of Exact Sciences”. 2, s. 101–135, czerwiec 1999. DOI: 10.1007/s004070050036. (ang.). {{Cytuj pismo}} Nieznane pola: "tom".
• Ivor Grattan-Guinness: The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press, 1970. ISBN 0-262-07034-0. (ang.).{{Cytuj książkę}} Nieznane pola: "link autor".brak strony w książce
• G.H. Hardy: Divergent Series. Clarendon Press, 1949. (ang.).{{Cytuj książkę}} Nieznane pola: "link autor".brak strony w książce
• Morris Kline. Euler and Infinite Series. „Mathematics Magazine”. 5, s. 307–314, listopad 1983. (ang.). {{Cytuj pismo}} Nieznane pola: "tom" oraz "link autor".
• Shaughan Lavine: Understanding the Infinite. Harvard UP, 1994. ISBN 0-674-92096-1. (ang.).brak strony w książce
• A.I. Markushevich: Series: fundamental concepts with historical exposition. Hindustan Pub. Corp., 1967. (ang.).brak strony w książce
• Saichev, A.I., and W.A. Woyczyński: Distributions in the physical and engineering sciences, Volume 1. Birkhaüser, 1996. ISBN 0-8176-3924-1. (ang.).brak strony w książce
• John Tucciarone. The development of the theory of summable divergent series from 1880 to 1925. „Archive for History of Exact Sciences”. 1-2, s. 1–40, styczeń 1973. DOI: 10.1007/BF00343405. (ang.). {{Cytuj pismo}} Nieznane pola: "tom".
• Anders Vretblad: Fourier Analysis and Its Applications. Springer, 2003. ISBN 0-387-00836-5. (ang.).brak strony w książce
• John E. Weidlich: Summability methods for divergent series. Stanford M.S. theses, czerwiec 1950. (ang.).brak strony w książce

Kategoria:Matematyka Kategoria:Paradoksy

[[bn:১ − ২ + ৩ − ৪ + · · ·]] [[ca:1 − 2 + 3 − 4 + ...]] [[da:1 − 2 + 3 − 4 + · · ·]] [[en:1 − 2 + 3 − 4 + · · ·]] [[es:1 − 2 + 3 − 4 + · · ·]] [[fa:۱ - ۲ + ۳ - ۴ +...]] [[fr:Série alternée des entiers]] [[it:1 − 2 + 3 − 4 + · · ·]] [[lv:1 − 2 + 3 − 4 + · · ·]] [[ja:1-2+3-4+…]] [[no:1 − 2 + 3 − 4 + · · ·]] [[pt:1 − 2 + 3 − 4 + · · ·]] [[sl:1 − 2 + 3 − 4 + · · ·]] [[fi:1 − 2 + 3 − 4 + · · ·]] [[th:1 − 2 + 3 − 4 + · · ·]] [[tr:1 − 2 + 3 − 4 + · · ·]] [[zh:1-2+3-4+…]]