Pomiary odległości (kosmologia)

Pomiary odległości – pomiary wykorzystywane do zobrazowania odległości pomiędzy obiektami astronomicznymi lub zdarzeniami we Wszechświecie. Są często wykorzystywane do powiązania pewnych obserwowalnych wielkości (jak jasność odległych kwazarów, przesunięcie ku czerwieni odległej galaktyki lub rozmiar kątowy pików akustycznych mikrofalowego promieniowania tła) z wielkościami, które nie są bezpośrednio obserwowalne, ale wygodniejsze do obliczeń (jak współrzędne współporuszające się kwazarów, galaktyk itp.). Metody pomiarów odległości opisane poniżej odnoszą się do odległości euklidesowych, przy niewielkim przesunięciu ku czerwieni.

Zgodnie z obecnym rozumieniem kosmologii, pomiary te są wykonywane w kontekście równań ogólnej teorii względności (OTW). W szczególności, w poniższych rozważaniach do opisu Wszechświata w największych skalach wykorzystuje się model Friedmana-Lemaître’a z metryką FLRW.

Przegląd metod

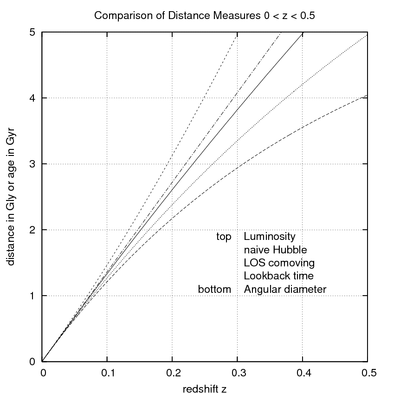
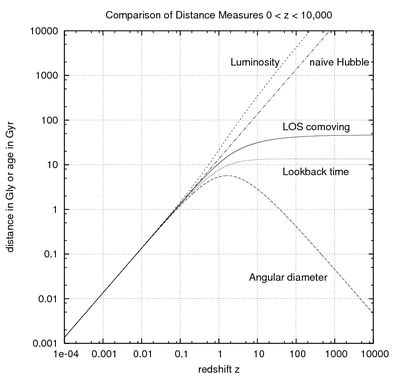
W kosmologii fizycznej istnieje kilka definicji „odległości”. Na ogół są one równoważne przy założeniu wystarczająco małych przesunięć ku czerwieni i wyraża się je w funkcji tej ostatniej wielkości. Dzięki temu można je wyznaczać w praktyce, gdyż redshift (z) jest podstawową wielkością mierzoną w kosmologii obserwacyjnej. Odległości te zapisuje się też jako funkcje czynnika skali $a=1/(1+z),$ czasu kosmicznego $t$ lub konforemnego $\eta$ dzięki prostym przekształceniom zmiennych. Związki pomiędzy poszczególnymi rodzajami odległości można wyrazić definiując bezwymiarowy parametr Hubble’a

$E(z)={\sqrt {\Omega _{m}(1+z)^{3}+\Omega _{k}(1+z)^{2}+\Omega _{\Lambda }}}$

i odległość Hubble’a $d_{H}=c/H_{0}.$ W podanych tu wzorach $\Omega _{m}$ jest bezwymiarową gęstością materii nierelatywistycznej, $\Omega _{\Lambda }$ jest gęstością ciemnej energii, $\Omega _{k}=1-\Omega _{m}-\Omega _{\Lambda }$ reprezentuje bezwymiarową krzywiznę czasoprzestrzeni, $H_{0}$ jest stałą Hubble’a, a $c$ prędkością światła w próżni. W kosmologii są powszechnie używane następujące pomiary odległości wzdłuż linii widzenia od obserwatora do obiektu o redshifcie $z{:}$

Odległość współporuszająca się:

$d_{C}(z)=d_{H}\int _{0}^{z}{\frac {dz'}{E(z')}}$

Transwersalna odległość współporuszająca się:

$d_{M}(z)=\left\{{\begin{array}{ll}{\frac {d_{H}}{\sqrt {\Omega _{k}}}}\sinh \left({\sqrt {\Omega _{k}}}d_{C}(z)/d_{H}\right)&{\text{dla }}\Omega _{k}>0\\d_{C}(z)&{\text{dla }}\Omega _{k}=0\\{\frac {d_{H}}{{\sqrt {|\Omega _{k}}}|}}\sin \left({\sqrt {|\Omega _{k}|}}d_{C}(z)/d_{H}\right)&{\text{dla }}\Omega _{k}<0\end{array}}\right.$

Odległość „średnicy kątowej”:

$d_{A}(z)={\frac {d_{M}(z)}{1+z}}$

Odległość jasnościowa:

$d_{L}(z)=(1+z)d_{M}(z)$

Droga przebyta przez światło:

$d_{T}(z)=d_{H}\int _{0}^{z}{\frac {dz'}{(1+z')E(z')}}$

Odległość współporuszającą się można otrzymać z transwersalnej odległości współporuszającej się w granicy $\Omega _{k}\to 0,$ co oznacza, że obie te odległości są równoważne w płaskim Wszechświecie.

Porównanie kosmologicznych pomiarów odległości, od redshiftu $z=0$ (czas obecny) do $z=0{,}5.$ Założenia kosmologiczne: stała Hubble’a wynosi 72 km/s/Mpc, $\Omega _{\Lambda }=0{,}732,$ $\Omega _{m}=0{,}266,$ $\Omega _{\mathrm {promieniowania} }=0{,}002$ i $\Omega _{k}=0$ (parametry gęstości tak dobrane, aby ich suma wynosiła 1).

Porównanie kosmologicznych pomiarów odległości, od redshiftu $z=0$ (czas obecny) do $z=10000,$ odpowiadającemu przejściu z ery promieniowania do ery materii. Założenia kosmologiczne: stała Hubble’a wynosi 72 km/s/Mpc, $\Omega _{\Lambda }=0{,}732,$ $\Omega _{m}=0{,}266,$ $\Omega _{\mathrm {promieniowania} }=0{,}002$ i $\Omega _{k}=0$ (parametry gęstości tak dobrane, aby ich suma wynosiła 1).

Nazewnictwo alternatywne

Peebles nazywa transwersalną odległość współporuszającą się „odległością rozmiaru kątowego” (nie mylić z odległością średnicy kątowej). Mimo że nie jest to kwestia nomenklatury, odległość współporuszająca się jest równoważna odległości ruchu własnego, która jest zdefiniowana jako iloraz prędkości transwersalnej i jej ruchu własnego w radianach w czasie. Okazjonalnie symbole $\chi$ lub $r$ są używane do oznaczenia obu odległości: współporuszającej się i średnicy kątowej. Droga przebyta przez światło jest czasami nazywana odległością „spojrzenia w przeszłość” (ang. lookback distance).

Szczegóły

Współrzędne współporuszające się

Dla obserwatora fundamentalnego znajdującego się w ustalonym punkcie określonym przez współrzędne współporuszające się, czas kosmiczny jest taki sam jak czas mierzony lokalnie. Odległość współporuszająca się jest dystansem jaki dzieli dwa punkty położone w układzie współrzędnych współporuszających się, przy takim samym czasie kosmicznym, mierzonym w obu tych punktach.

W czasie kiedy światło będzie się przemieszczać od obiektu do obserwatora, Wszechświat będzie się rozszerzał, więc fotony przebędą odpowiednio dłuższą drogę, niż wynosi odległość współporuszająca się pomiędzy obiektem a obserwatorem (o ile poruszać się będzie po geodezyjnej). Na przykład światło z galaktyki z8 GND 5296 podróżowało do Ziemi ponad 13 miliardów lat (odległość/droga przebyta przez światło), a współcześnie sama galaktyka według współrzędnych współporuszających się oddalona jest o około 30 miliardów lat świetlnych od Ziemi.

Transwersalna odległość współporuszająca się

Dwa współporuszające się obiekty o stałym przesunięciu ku czerwieni $z,$ oddalone na niebie o kąt $\delta \theta ,$ dzieli dystans $\delta \theta d_{M}(z),$ gdzie $d_{M}$ oznacza transwersalną odległość współporuszającą się.

Odległość średnicy kątowej

Obiekt o rozmiarze $x$ przy redshifcie $z$ posiadający rozmiar kątowy $\delta \theta$ znajduje się w odległości średnicy kątowej $d_{A}(z)=x/\delta \theta .$ Jest ona powszechnie wykorzystywana do obserwacji tzw. linijek standardowych, np. na tle akustycznych oscylacji barionów.

Odległość jasnościowa

Jeżeli znana jest rzeczywista jasność odległego obiektu, to można obliczyć odległość jasnościową do niego przez pomiar strumienia $S$ i określenie $d_{L}(z)={\sqrt {L/4\pi S}},$ która jest równoważna $d_{L}(z)$ z wyrażenia powyżej. Wartość ta jest istotna dla pomiarów świec standardowych, takich jak supernowe typu Ia, które pierwsze zostały wykorzystane do odkrycia przyśpieszenia ekspansji Wszechświata.

Droga przebyta przez światło

Ta odległość jest czasem, w którym światło dotarło od obiektu do obserwatora, pomnożonym przez prędkość światła. Np. światło od Betelgezy biegnie do obserwatora na Ziemi w przeciągu ok. 500 lat. Mnożąc ten czas przez prędkość światła otrzymujemy wartość 500 lat świetlnych, czyli 4,73·10¹⁵ metrów (4730 bilionów kilometrów).

Zobacz też

• drabina odległości kosmicznych
• Wielki Wybuch

Bibliografia

• David W.D.W. Hogg David W.D.W., Distance measures in cosmology, „arXiv”, 2000, DOI: 10.48550/arXiv.astro-ph/9905116, arXiv:astro-ph/9905116v4  (ang.).
• P.J.E.P.J.E. Peebles P.J.E.P.J.E., Principles of Physical Cosmology, Princeton University Press, 1993 .brak strony (książka)
• ScottS. Dodelson ScottS., Modern Cosmology, Academic Press, 2003 .brak strony (książka)

Linki zewnętrzne

• Skala odległości we Wszechświecie (ang.)
• iCosmos: Kalkulator kosmologiczny (z wykresami) (ang.)