Drabina odległości kosmicznych
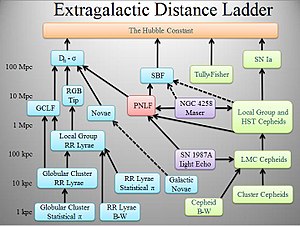
Techniki odpowiednie dla galaktyk gwiazdotwórczych.
Techniki odpowiednie dla galaktyk II populacji.
Geometryczne techniki odległości.
Technika PNLF odpowiednia dla wszystkich populacji Supergromady w Pannie.
Linia ciągła: Dobrze wyskalowany szczebel drabiny. Linia przerywana: Niepewna (niedokładna) skala szczebla drabiny.Drabina odległości kosmicznych – szereg metod, którymi astronomowie określają odległości do obiektów astronomicznych. Prawdziwy bezpośredni pomiar odległości do ciała niebieskiego jest możliwy tylko dla tych obiektów, które są wystarczająco blisko (około tysiąca parseków) od Ziemi. Techniki określania odległości do bardziej oddalonych obiektów opierają się na różnych korelacjach pomiędzy metodami poprawnymi dla mniejszych odległości a metodami, które działają dla dalszych. Kilkanaście metod opiera się na świecach standardowych, które są obiektami astronomicznymi o znanej jasności[a] (absolutnej wielkości gwiazdowej).
Analogia z drabiną wzięła się z faktu, iż żadna technika nie umożliwia pomiaru we wszystkich skalach odległości spotykanych w astronomii. Pewne metody mogą być użyte do pomiarów bliskich odległości, inne do pomiarów zakresów od bliskich do średnich itd. Każdy szczebel drabiny dostarcza informacji, która z metod może być użyta do określenia odległości na następnym, wyższym szczeblu.
Pomiar bezpośredni[edytuj | edytuj kod]
U podstawy drabiny znajdują się fundamentalne metody pomiaru odległości, w których są one mierzone bezpośrednio, bez rozstrzygania pytań o naturze obiektów. Precyzyjnymi pomiarami pozycji gwiezdnych zajmuje się astrometria.

Jednostka astronomiczna[edytuj | edytuj kod]
Bezpośrednie pomiary odległości są oparte na precyzyjnym określeniu odległości pomiędzy Ziemią a Słońcem, zwanej jednostką astronomiczną (j.a., ang. au). W przeszłości, dla określenia wartości j.a. kluczowe były obserwacje tranzytu Wenus, a w pierwszej połowie XX w. również obserwacje asteroid. W XXI wieku jednostka astronomiczna jest mierzona z wysoką precyzją za pomocą pomiarów radarowych Wenus oraz innych bliskich planet i planetoid[1], a także poprzez śledzenie międzyplanetarnych pojazdów na ich orbitach wokół Słońca i w Układzie Słonecznym. Wprawdzie prawa Keplera dostarczają precyzyjnych współczynników rozmiarów orbit obiektów obiegających Słońce, ale nie mierzą rzeczywistych rozmiarów tych orbit. Radar umożliwia pomiar różnic w rozmiarach dwóch orbit z dokładnością kilometrów i z tych danych oraz ze współczynników rozmiarów dwóch orbit obliczana jest dokładna długość orbity Ziemi.
Paralaksa[edytuj | edytuj kod]
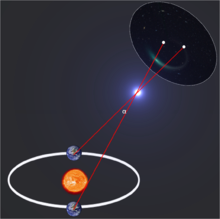
Najważniejszym podstawowym pomiarem odległości jest paralaksa pochodząca z trygonometrii. Ponieważ Ziemia orbituje wokół Słońca, pozycja pobliskich gwiazd będzie wydawać się lekko przesunięta, tym mniej im dalej się one znajdują. Te przesunięcia są kątami trójkąta równoramiennego, którego krótszy bok ma długość 2 j.a. a dłuższy jest odległością do gwiazdy. Wartość przesunięcia jest bardzo mała, 1′′ łuku dla obiektów oddalonych o 1 parsek (3,26 roku świetlnego) i mniejsza wartość kąta oznacza większą odległość. Najbliższa Słońcu gwiazda alfa Centauri znajduje się w odległości 4,37 roku świetlnego.
Ponieważ paralaksa pomniejsza się dla większych odległości gwiezdnych, za jej pomocą mierzone są te odległości do gwiazd, których paralaksa jest większa niż precyzja samego pomiaru. Pomiar paralaktyczny ma zazwyczaj dokładność ułamków sekund kątowych[2]. Na przykład w latach 90. XX wieku misja Hipparcos zmierzyła paralaksy setek gwiazd (odległych o kilkaset parseków) z precyzją rzędu 0.7-0.9 milisekund kątowych[3].
Gwiazdy mogą poruszać się względem Słońca z prędkością względną, powodującą ruch własny i prędkość radialną. Ich wzorzec ruchu jest określany poprzez odnotowywanie ich pozycji na przestrzeni wielu lat, a ostateczna odległość przez pomiar przesunięcia dopplerowskiego ich spektrum wzdłuż linii wzroku (obserwacji). Dla grup gwiazd tej samej klasy spektralnej i o podobnej jasności średnią paralaksę można uzyskać z analiz statystycznych ich ruchu własnego względem ich prędkości radialnej. Ta metoda paralaksy statystycznej jest przydatna w pomiarach odległości do jasnych gwiazd, odległych o ponad 50 pc oraz do olbrzymich gwiazd zmiennych, jak cefeidy czy RR Lyrae[4].
Świece standardowe[edytuj | edytuj kod]
Prawie wszystkie mierniki fizycznych odległości są świecami standardowymi. Są to obiekty należące do pewnej klasy o znanej jasności. Poprzez porównanie znanej jasności pewnego obiektu z obserwowaną jasnością obiektu badanego można za pomocą prawa odwrotności kwadratów obliczyć odległość do niego.
W astronomii jasność danego obiektu jest podana jako absolutna wielkość gwiazdowa, czyli jasność, jaką miałyby, znajdując się w odległości 10 parseków (32,6 lat świetlnych) od obserwatora. Natomiast obserwowana wielkość gwiazdowa może być wykorzystana do określenia odległości do obiektu (w kiloparsekach) za pomocą równania:
gdzie to obserwowana, a to absolutna wielkość gwiazdowa. Równanie powyższe ma sens tylko wtedy, gdy obie wielkości są mierzone w tej samej częstotliwości pasma i nie ma ruchu względnego w kierunku radialnym.
Są również konieczne pewne uśrednienia obliczeń uwzględniające ekstynkcję (która powoduje, że obiekty wydają się bardziej oddalone i poczerwienione), zwłaszcza jeśli obiekt leży w regionie zawierającym sporo pyłu lub gazu[5]. Różnica pomiędzy wielkością absolutną i obserwowaną nosi nazwę modułu odległości i odległości astronomiczne, zwłaszcza międzygalaktyczne, są czasami podawane z uwzględnieniem tego modułu.
Problemy[edytuj | edytuj kod]

Ze stosowaniem świec standardowych (dowolnej klasy) występują dwa problemy. Głównym jest kalibracja, czyli dokładne określenie wielkości absolutnej świecy. Obejmuje to dobre zdefiniowanie klasy obiektów, której członkowie mogą być rozpoznani (określeni) i znalezienie odpowiedniej liczby członków klasy, do których odległości są zmierzone, a których wielkość absolutna może być określona z wystarczającą dokładnością. Drugi problem leży w określeniu członków klasy, a konkretnie w uniknięciu pomyłki polegającej na kalibracji przy wykorzystaniu świecy standardowej obiektu, który do klasy nie należy. Dla bardzo dalekich odległości, gdzie najbardziej wskazane jest użycie wskaźnika odległości, może to stanowić bardzo poważny problem.
Istotnym wyzwaniem przy korzystaniu ze świec standardowych jest odpowiedź na pytanie, jak standardowe one są. Np. wszystkie obserwacje wydają się świadczyć, że supernowe typu Ia, których odległość jest znana, mają tę samą wielkość gwiazdową (z poprawką na zakrzywienie światła). Zasada ta jest opisana poniżej, ale mimo to istnieje możliwość, że bardziej odległe supernowe typu Ia mają inne własności niż te bliższe. Wykorzystanie supernowych Ia jest kluczowe do określenie właściwego modelu kosmologicznego. Jeżeli pożądane właściwości supernowych Ia są inne dla dalszych odległości, np. jeżeli ekstrapolacja ich kalibracji do danych odległości nie jest prawidłowa, ignorowanie tej zmienności może generować systematyczny błąd przy rekonstruowaniu parametrów kosmologicznych, w szczególności gęstości materii[6].
Historia pomiarów odległości za pomocą zmiennych cefeid pokazuje, że nie jest to jedynie problem teoretyczny. W latach 50. XX wieku Walter Baade odkrył, że pobliskie cefeidy, użyte do kalibracji świecy standardowej były innego typu, niż te użyte do pomiarów odległości do pobliskich galaktyk. Cefeidy były gwiazdami I populacji, o wiele większej metaliczności niż bardziej odległe gwiazdy II populacji. W rezultacie, gwiazdy II populacji były de facto o wiele jaśniejsze niż sądzono, co spowodowało efekt podwojenia odległości do gromad kulistych, bliskich galaktyk, jak i średnicy Drogi Mlecznej.
Linijka standardowa[edytuj | edytuj kod]
Innym rodzajem miernika fizycznej odległości jest linijka standardowa. W 2008 jako możliwą linijkę standardową do określania parametrów kosmologicznych zaproponowano przyjąć średnice galaktyk[7].
Mierniki odległości galaktycznych[edytuj | edytuj kod]
Oprócz kilku wyjątków, odległości oparte na pomiarach bezpośrednich są możliwe jedynie w obszarze do tysiąca parseków, który jest niewielkim wycinkiem naszej Galaktyki. Dla obszarów poza nią, pomiary zależą od założeń fizycznych, tzn. wspomnianego warunku, że rozpoznajemy obiekt oraz że klasa obiektów jest wystarczająco jednorodna, aby jej członkowie mogliby być użyci do sensownego oszacowania odległości.
Fizyczne mierniki odległości wykorzystywane do stopniowo dalszych skal odległości obejmują:
- dynamiczną paralaksę – wykorzystanie parametrów orbitalnych układów wizualnie podwójnych do mierzenia masy systemu oraz stosunku masy do jasności do określenia jasności
- układy zaćmieniowe gwiazd podwójnych – pomiary tych układów stały się możliwe dzięki teleskopom 8-metrowym, co uczyniło je jednocześnie możliwymi miernikami odległości. Zostały wykorzystane m.in. do oszacowania bezpośrednich odległości do Obłoków Magellana, galaktyki Andromedy i Trójkąta. Układy zaćmieniowe umożliwiają bezpośrednią metodę szacowania odległości do galaktyk z dokładnością powiększoną o 5%, co przekłada się na zakres odległości do około 3 Mpc[8].
- gwiazdy zmienne typu RR Lyrae – czerwone olbrzymy zazwyczaj są używane do pomiarów odległości w Galaktyce i do pobliskich gromad kulistych.
- Do pomiarów odległości do starych populacji gwiezdnych (II populacji) używane są[9]:
- Wskaźnik TRGB (ang. tip of the red giant branch) – związany z jasnością czerwonych olbrzymów
- Funkcja jasności mgławic planetarnych (PNLF)
- Funkcja jasności gromad kulistych (GCLF)
- Fluktuacje jasności powierzchniowej (SBF)
- Emisje promieni X bersterów – emisje te (termonuklearne błyski na powierzchni gwiazdy neutronowej) wykorzystywane są jako świece standardowe. Obserwacje pasma promieni X w tych wybuchach czasami wskazują na ekspansje rozmiaru (promienia) obiektu i stąd strumień promieni X w piku emisji powinien być związany z jasnością Eddingtona, która z kolei może zostać obliczona, o ile znana jest masa gwiazdy neutronowej (powszechnie przyjmowanym założeniem jest 1,5 M☉). Ta metoda pozwala na określenie odległości do niektórych rentgenowskich układów podwójnych. Takie układy o małej masie są słabo widoczne w paśmie optycznym, co czyni pomiary ich odległości bardzo trudnymi.
- Masery międzygwiezdne – mogą być użyte do uzyskania odległości do obiektów galaktycznych (a nawet niektórych pozagalaktycznych) dzięki emisji maserowej.
- Cefeidy i nowe
- Poszczególne galaktyki w gromadach
- Związek Tully’ego-Fishera
- Związek Faber-Jacksona
- Supernowe Ia – mają bardzo dobrze określoną maksymalną absolutną wielkość gwiazdową jako funkcję kształtu ich krzywej blasku i są przydatne w określaniu pozagalaktycznych odległości do kilkuset Mpc[10] (wyjątkiem jest SN 2003fg, supernowa Ia o nietypowej naturze)
- Przesunięcie ku czerwieni i prawo Hubble’a
Dopasowanie na podstawie ciągu głównego[edytuj | edytuj kod]
Umieszczając na wykresie wielkość absolutną grupy gwiazd oraz ich typ widmowy, na podstawie diagramu Hertzsprunga-Russella można rozpoznać wzorce ewolucyjne, związane z masą, wiekiem i składem gwiazd. W szczególności, podczas spalania wodoru gwiazdy układają się wzdłuż krzywej, zwanej ciągiem głównym. Poprzez mierzenie tych wartości ze spektrum gwiazdy, można określić pozycję gwiazdy na diagramie H-R, a stąd można oszacować jej absolutną wielkość gwiazdową. Porównanie tych wartości z wielkością obserwowaną pozwala na oszacowanie odległości do niej, po odpowiedniej korekcie uwzględniającej ekstynkcję jasności z powodu gazu i pyłu.
W związanej grawitacyjnie gromadzie gwiazd, takiej jak Hiady, gwiazdy są formowane mniej więcej w tym samym okresie i leżą w tej samej odległości od nas. Pozwala to na dokładne dopasowanie na podstawie ciągu głównego, umożliwiając określenie zarówno wieku, jak i odległości.
Pozagalaktyczna skala odległości[edytuj | edytuj kod]
Pozagalaktyczna skala odległości jest serią technik, wykorzystywanych do określania odległości do obiektów poza naszą galaktyką, które nie są łatwe do uzyskania metodami tradycyjnymi. Niektóre procedury wykorzystują właściwości takich obiektów gwiazdy, gromady kuliste, mgławice i całe galaktyki. Inne metody mają charakter statystyczno-probabilistyczny.
| Metoda | Niedokładność dla pojedynczej galaktyki (mag) | Odległość do gromady w Pannie (Mpc) | Zakres (Mpc) |
|---|---|---|---|
| Cefeidy I populacji | 0,16 | 15–25 | 29 |
| Nowe | 0,4 | 21,1 ± 3,9 | 20 |
| Funkcja jasności mgławic planetarnych (PNLF) | 0,3 | 15,4 ± 1,1 | 50 |
| Funkcja jasności gromad kulistych (GCLF) | 0,4 | 18,8 ± 3,8 | 50 |
| Fluktuacje jasności powierzchniowej (SBF) | 0,3 | 15,9 ± 0,9 | 50 |
| Zależność D – σ | 0,5 | 16,8 ± 2,4 | < 100 |
| Supernowe Ia | 0,10 | 19,4 ± 5,0 | < 1000 |

Efekt Wilsona-Bappu[edytuj | edytuj kod]
Odkryty w 1956 przez Olina Wilsona i Vainu Bappu efekt Wilsona-Bappu wykorzystuje zjawisko znane jako paralaksa spektroskopowa. Określone gwiazdy posiadają własności w swoich spektrach emisyjno-absorpcyjnych, pozwalające na względnie proste obliczenie ich wielkości absolutnej. Określone linie spektralne są bezpośrednio związane z jasnością obiektu, np. linia absorpcyjna K wapnia. Odległość do gwiazdy może zostać obliczona z jasności dzięki modułowi odległości:
Choć teoretycznie ta metoda powinna umożliwiać wiarygodne obliczenia odległości do gwiazd nawet w skali 7 Mpc, to na ogół stosuje się do gwiazd odległych o setki kiloparseków. Ma ona zastosowanie jedynie dla gwiazd o jasności powyżej 15m.
Klasyczne Cefeidy[edytuj | edytuj kod]
Dla obiektów poza zasięgiem efektu Wilsona-Bappu stosuje się metodę, opartą na związku okresowej jasności klasycznych cefeid, odkrytą przez Henriettę Leavitt. Związek ten może być wykorzystany do obliczania odległości zarówno do galaktycznych, jak i pozagalaktycznych klasycznych cefeid:

Wykorzystanie cefeid jako świec standardowych jest przedmiotem ciągłych rozważań, gdyż metody te komplikuje szereg problemów, spośród których najważniejszymi są: powiązanie natury i liniowości okresowych jasności w różnych pasmach oraz wpływ metaliczności na punkt początkowy i nachylenie wykresu tego powiązania, efektów kontaminacji fotometrycznej (mieszania) i wpływu (zazwyczaj nieznanego) prawa ekstynkcji na odległości do cefeid[13][14][15][16][17][18][19][20][21].
Te nierozwiązanie zagadnienia skutkują tym, że wartość stałej Hubble’a, spotykana w pracach waha się pomiędzy 60 km/s/Mpc a 80 km/s/Mpc. Rozwiązanie tej rozbieżności jest jednym z głównych problemów astronomii, ponieważ parametry kosmologiczne Wszechświata mogą być silnie zależne od precyzyjnej wartości stałej Hubble’a[22][23].
Zmienne cefeidy były podstawowym instrumentem, za pomocą którego Edwin Hubble w 1923 wysnuł wniosek, że M31 (Andromeda) była osobną galaktyką, a nie małą mgławicą w Drodze Mlecznej oraz oszacował do niej odległość na 285 kpc (obecna wartość to 773 kpc).
Odkryto, że NGC 3370, spiralna galaktyka w gwiazdozbiorze Lwa, zawiera najbardziej odległe cefeidy dotychczas zaobserwowane, znajdujące się w odległości 29 Mpc. Zmienne cefeidy nie są idealnymi miernikami odległości, posługiwanie się nimi generuje około 7% błąd dla pobliskich galaktyk i do 15% przy większych dystansach.
Supernowe[edytuj | edytuj kod]

Istnieje kilkanaście różnych metod wykorzystania supernowych do pomiaru pozagalaktycznych odległości, poniżej są wymienione najczęściej używane.
Pomiary fotosfery supernowej[edytuj | edytuj kod]
Można założyć, że supernowa rozszerza (ekspanduje) w sposób symetryczny. Jeżeli znajduje się dostatecznie blisko, to można zmierzyć rozmiar kątowy jej fotosfery
gdzie jest prędkością kątową. Aby dokonać dokładnego pomiaru, konieczne jest wykonanie co najmniej dwóch obserwacji, które dzieli czas Następnie
gdzie jest odległością do supernowej, prędkością radialną wyrzucanej (ang. ejecta) materii (dla sferycznie symetrycznego zjawiska można założyć, że ).
Ta metoda działa tylko w przypadku, gdy supernowa jest dostatecznie blisko, aby można było dokładnie zmierzyć jej fotosferę. W rzeczywistość powłoka gazowa nie jest idealnie sferyczna, ani nie jest ciałem doskonale czarnym. Również ekstynkcja międzygwiazdowa zaburza dokładność pomiarów, a dodatkowo problem jest zwiększany przez kolaps jądra supernowej. Wszystkie te czynniki mogą powiększyć błąd pomiaru odległości nawet o 25%.

Krzywe blasku supernowych Ia[edytuj | edytuj kod]
Supernowe typu Ia są jednymi z najlepszych źródeł do wyznaczania międzygalaktycznych odległości. Zjawisko to występuje, kiedy w układzie podwójnym na białego karła opada materia z towarzyszącej mu gwiazdy (zazwyczaj czerwonego olbrzyma), skutkiem czego biały karzeł w końcu osiąga granicę Chandrasekhara (1,44 M☉). Wówczas gwiazda staje się niestabilna, gdyż rozpoczyna się gwałtowna reakcja termojądrowa. Ponieważ wszystkie eksplodujące supernowe Ia mają tę samą masę, ich absolutne wielkości gwiazdowe są również te same, co czyni je bardzo użytecznymi świecami standardowymi. Wszystkie supernowe Ia mają standardową magnitudę w paśmie niebieskim i widzialnym:
Dlatego podczas obserwacji tych gwiazd możliwe jest określenie piku ich jasności, a na jego podstawie odległości. W zasadzie nie jest konieczne uchwycenie piku w momencie obserwacji – wykorzystując metodę wielobarwnej krzywej blasku (ang. multicolor light curve shape – MLCS) kształt krzywej (uzyskany w rozsądnym czasie po początkowej eksplozji) jest porównywany z podobnymi sparametryzowanymi wykresami, co pozwala określić absolutną wielkość przy maksymalnej jasności. Ta metoda uwzględnia jednocześnie ekstynkcję pyłu i gazu.

Również metoda „kompresowania” („przeciągania”) (ang. stretch method) dopasowuje poszczególne krzywe brzasku do wzorca. W przeciwieństwie do metody MLCS, zamiast kilkunastu krzywych blasku dla różnych długości fali mamy jedną krzywą, która została „skompresowana” w czasie, a dzięki „czynnikowi kompresji” (ang. stretch factor) można określić pik magnitudy[24].
Wykorzystanie supernowych typu Ia jest jedną z najdokładniejszych metod, zwłaszcza odkąd ich eksplozje stały się możliwe do obserwowania na dużych odległościach (ich jasności dorównują galaktykom, w których się znajdują), znacznie większych (około 500 razy) niż cefeidy. Bieżąca niedokładność tych pomiarów zwykle wynosi 5%, co przekłada się na jedynie 0,1 m.
Nowe[edytuj | edytuj kod]
Nowe mogą być użyte do pomiarów odległości pozagalaktycznych w taki sam sposób, jak supernowe. Istnieje bezpośredni związek pomiędzy maksymalną jasnością nowej i czasu, w którym jej wielkość gwiazdowa w świetle widzialnym zmniejsza się o 2 magnitudy:
gdzie jest pochodną czasu magnitudy nowej, opisującym średni wskaźnik jej zmniejszania się o pierwsze 2 magnitudy.
Gdy nowe gasną, są prawie tak samo jasne jak najjaśniejsze cefeidy i dlatego obie te metody mogą być stosowane na podobnych odległościach: ~20 Mpc. Błąd tej metody powoduje niedokładność wielkości gwiazdowej około ± 0,4.
Funkcja jasności gromad kulistych[edytuj | edytuj kod]

Opierając się na metodzie porównywania jasności gromad kulistych (zlokalizowanych w halo galaktycznym) z odległych galaktyk do tych z gromady w Pannie, funkcja jasności gromad kulistych (ang. globular cluster luminosity function – GCLF) generuje błąd pomiaru odległości około 20% (0,4 m).
Amerykański astronom William Alvin Baum pierwszy podjął próbę użycia gromad kulistych do pomiaru odległych galaktyk eliptycznych. Porównał najjaśniejsze gromady kuliste w Pannie A z gromadami w Andromedzie zakładając, że jasności gromad są takie same w obu galaktykach. Znając odległość do Andromedy, Baum założył bezpośrednią korelację i oszacował odległość do Panny A.
Baum użył tylko jednej gromady kulistej, a pojedyncze formacje są często słabymi świecami standardowymi. Kanadyjski astronom René Racine przyjął, że zastosowanie funkcji jasności gromad kulistych (ang. globular cluster luminosity functionx – GCLF) mogłoby dać lepsze przybliżenie. Ilość gromad kulistych jako funkcja jasności jest określona przez:
gdzie jest jasnością rotacji, jest jasnością gromady Panny, a jest dyspersją ~ 1,4 m.
Należy pamiętać o założeniu, że wszystkie gromady kuliste mają mniej więcej te same magnitudy we Wszechświecie. Nie istnieje uniwersalna funkcja jasności gromad kulistych, którą można zastosować do wszystkich galaktyk.
Funkcja jasności mgławic planetarnych[edytuj | edytuj kod]
Podobną metodzie GCLF analizę numeryczną można użyć dla mgławic planetarnych w bardzo dalekich galaktykach. Funkcja jasności mgławic planetarnych (ang. planetary nebula luminosity function – PNLF) po raz pierwszy została zaproponowana w późnych latach 70h przez Hollanda Cole’a i Dawida Jennera. Zasugerowali oni, że wszystkie mgławice planetarne mogą mieć podobną absolutną wielkość gwiazdową (obecnie szacowaną na M = -4,53), co mogłoby z nich uczynić świece standardowe do określania pozagalaktycznych odległości.
Astronom George Jacoby wraz ze współpracownikami zaproponowali funkcję PNLF[25]:
gdzie jest liczbą mgławic planetarnych, posiadających wielkość absolutną a jest absolutną wielkością najjaśniejszej mgławicy.
Fluktuacje jasności powierzchniowej[edytuj | edytuj kod]
Metodę fluktuacji jasności powierzchniowej (ang. surface brightness fluctuation – SBF) zaproponowano w 1990 r. podczas pomiarów magnitud 14 młodych galaktyk (głównie z gromady w Pannie) za pomocą teleskopu w Kitt Peak[26].
Technika wykorzystuje kamery CCD instalowane przy teleskopach. Z uwagi na fluktuacje jasności powierzchniowej galaktyki, niektóre piksele kamery rejestrują więcej gwiazd niż inne i jeśli odległość do obiektu się zwiększa to obraz wydaje się „gładszy”. Wariancja jasności piksel do piksela jest związana z odległością do galaktyki – im większe fluktuacje tym bliższy obiekt (inaczej: galaktyka dwa razy odleglejsza wygląda na zdjęciu na dwa razy gładszą[27]).

SBF została skalibrowana za pomocą okresowej jasności cefeid w Wielkim Obłoku Magellana. Umożliwia szacowanie odległości nawet większych niż 100 Mpc, ale ze sporymi błędami, dlatego zazwyczaj jest stosowana do obszarów nieco mniejszych.
Zależność D-σ[edytuj | edytuj kod]
Zależność D-σ, występująca w galaktykach eliptycznych, wiąże średnicę kątową galaktyki (D) z jej dyspersją prędkości (σ)[28]. Jasność powierzchniowa galaktyki jest niezależna od odległości do niej, ale średnica kątowa D jest do niej odwrotnie proporcjonalna:
gdzie C jest stałą zależną od odległości do gromady.
Dlatego też ta zależność nie ma charakteru świecy standardowej, wartość D stanowi raczej linijkę standardową.
Metoda ta ma potencjał, aby zostać jednym z najsilniejszych mechanizmów szacowania odległości międzygalaktycznych, możliwe, że przekraczającym swoim zasięgiem metodę Tully’ego-Fischera. Z drugiej strony galaktyki eliptyczne nie są dziś wystarczająco jasne do skalibrowania metody poprzez techniki takie jak cefeidy i metodę kalibruje się sposobami bardziej „surowymi” (niedopracowanymi).
Wady drabiny[edytuj | edytuj kod]
Ponieważ bardziej odległe „szczeble” drabiny zależą od tych bliższych, to metody użyte dla dalszych odległości zawierają błędy szczebli bliższych, zarówno systematyczne, jak i statystyczne. W wyniku propagacji tych błędów dokładność pomiarów odległości do dalszych obiektów jest dużo niższa niż do bliższych.
Zobacz też[edytuj | edytuj kod]
Uwagi[edytuj | edytuj kod]
- ↑ O ile nie zaznaczono inaczej, pojęcia jasność, wielkość i magnituda oznaczają w tym artykule wielkość gwiazdową.
- ↑ Na podstawie Jacoby i inni. A critical review of selected techniques for measuring extragalactic distances. „Publications”. 104, s. 599–662, 1992-08. ASoP. DOI: 10.1086/133035. ISSN 0004-6280. (ang.).
Przypisy[edytuj | edytuj kod]
- ↑ Ash, M.E., Shapiro, I.I., & Smith, W.B., 1967 Astronomical Journal, 72, 338-350.
- ↑ Staff: Trigonometric Parallax. [w:] The SAO Encyclopedia of Astronomy [on-line]. Swinburne Centre for Astrophysics and Supercomputing. [dostęp 2008-10-18]. (ang.).
- ↑ M.A.C. Perryman, et al.. The HIPPARCOS Catalogue. „Astronomy and Astrophysics”. 323, s. L49–L52, 1999. Bibcode: 1997A&A...323L..49P. (ang.).
- ↑ Baidyanath Basu: An Introduction to Astrophysics. PHI Learning Private Limited, 2003. ISBN 81-203-1121-3. (ang.).
- ↑ Type Ia Supernova. [w:] Weekly Topic [on-line]. Caglow. [dostęp 2012-01-30]. (ang.).
- ↑ Sebastian Linden, Jean-Marc Virey, André Tilquin. Cosmological parameter extraction and biases from type Ia supernova magnitude evolution. „A&A”. 506 (3), s. 1095–1105, 2009. DOI: 10.1051/0004-6361/200912811. Bibcode: 2009A&A...506.1095L. (ang.).
- ↑ C. Marinoni, A. Saintonge, R. Giovanelli, M.P. Haynes i inni. Geometrical tests of cosmological models. I. Probing dark energy using the kinematics of high redshift galaxies. „A&A”. 478 (1), s. 43–55, 2008. DOI: 10.1051/0004-6361:20077116. Bibcode: 2008A&A...478...43M. (ang.).
- ↑ Bonanos, Alceste Z. Eclipsing Binaries: Tools for Calibrating the Extragalactic Distance Scale. „Binary Stars as Critical Tools and Tests in Contemporary Astrophysics, International Astronomical Union. Symposium no. 240, 22–25 sierpnia 2006 Praga, Czechy, S240, #008”. 2, s. 79–87, 2006. DOI: 10.1017/S1743921307003845. Bibcode: 2007IAUS..240...79B. (ang.).
- ↑ Ferrarese, Laura; Ford, Holland C.; Huchra, John; Kennicutt, Robert C., Jr.; Mould, Jeremy R.; Sakai, Shoko; Freedman, Wendy L.; Stetson, Peter B.; Madore, Barry F.; Gibson, Brad K.; Graham, John A.; Hughes, Shaun M.; Illingworth, Garth D.; Kelson, Daniel D.; Macri, Lucas; Sebo, Kim; Silbermann, N. A. A Database of Cepheid Distance Moduli and Tip of the Red Giant Branch, Globular Cluster Luminosity Function, Planetary Nebula Luminosity Function, and Surface Brightness Fluctuation Data Useful for Distance Determinations. „The Astrophysical Journal Supplement Series”. 128 (2), s. 431–459, 2000. DOI: 10.1086/313391. Bibcode: 2000ApJS..128..431F. (ang.).
- ↑ S.A. Colgate. Supernovae as a standard candle for cosmology. „Astrophysical Journal”. 232 (1), s. 404–408, 1979. DOI: 10.1086/157300. Bibcode: 1979ApJ...232..404C. (ang.).
- ↑ Benedict, G. Fritz i inni. Hubble Space Telescope Fine Guidance Sensor Parallaxes of Galactic Cepheid Variable Stars: Period-Luminosity Relations. „The Astronomical Journal”. 133 (4), s. 1810–1827, 2007. (ang.).
- ↑ Majaess, Daniel; Turner, David; Moni Bidin, Christian; Mauro, Francesco; Geisler, Douglas; Gieren, Wolfgang; Minniti, Dante; Chené, André-Nicolas; Lucas, Philip; Borissova, Jura; Kurtev, Radostn; Dékány, Istvan; Saito, Roberto K. New Evidence Supporting Membership for TW Nor in Lyngå 6 and the Centaurus Spiral Arm. „The Astronomical Journal Letters”. 741 (2 (id. art. L2)), 2011. Bibcode: 2011ApJ...741L..27M. (ang.).
- ↑ Stanek, K. Z. The Optical Gravitational Lensing Experiment. Investigating the Influence of Blending on the Cepheid Distance Scale with Cepheids in the Large Magellanic Cloud. „Eprint arXiv:astro-ph/9909346”, s. 9346, 1999. Bibcode: 1999astro.ph..9346S. (ang.).
- ↑ Udalski, A., Pietrzynski, G., Szewczyk, O. i inni. The Optical Gravitational Lensing Experiment. Cepheids in the Galaxy IC1613: No Dependence of the Period-Luminosity Relation on Metallicity. „Acta Astronomica”. 51, s. 221, 2001. Bibcode: 2001AcA....51..221U. (ang.).
- ↑ Ngeow, C. The Hubble Constant from Type Ia Supernovae Calibrated with the Linear and Nonlinear Cepheid Period-Luminosity Relations. „The Astrophysical Journal”. 642, s. L29, 2006. DOI: 10.1086/504478. Bibcode: 2006ApJ...642L..29N. (ang.).
- ↑ Macri, L.M., Bersier, D., Greenhill, L.J. i inni. A New Cepheid Distance to the Maser-Host Galaxy NGC 4258 and Its Implications for the Hubble Constant. „The Astrophysical Journal”. 652 (2), s. 1133, 2006. DOI: 10.1086/508530. Bibcode: 2006ApJ...652.1133M. (ang.).
- ↑ Bono, G., Fiorentino, G., Marconi, M. i inni. Cepheids in External Galaxies. I. The Maser-Host Galaxy NGC 4258 and the Metallicity Dependence of Period-Luminosity and Period-Wesenheit Relations. „The Astrophysical Journal”. 684, s. 102, 2008. DOI: 10.1086/589965. Bibcode: 2008ApJ...684..102B. (ang.).
- ↑ Majaess, D., Lane, D. Type II Cepheids as Extragalactic Distance Candles. „Acta Astronomica”. 59, s. 403, 2009. Bibcode: 2009AcA....59..403M. (ang.).
- ↑ Madore, Barry F. Concerning the Slope of the Cepheid Period-Luminosity Relation. „The Astrophysical Journal”. 696 (2), s. 1498, 2009. DOI: 10.1088/0004-637X/696/2/1498. Bibcode: 2009ApJ...696.1498M. (ang.).
- ↑ Scowcroft, V., Mould, J.R., Wood, P. R. The effect of metallicity on Cepheid magnitudes and the distance to M33. „Monthly Notices of the Royal Astronomical Society”. 396 (3), s. 1287, 2009. DOI: 10.1111/j.1365-2966.2009.14822.x. Bibcode: 2009MNRAS.396.1287S. (ang.).
- ↑ Majaess, D. The Cepheids of Centaurus A (NGC 5128) and Implications for H0. „Acta Astronomica”. 60, s. 121, 2010. Bibcode: 2010AcA....60..121M. (ang.).
- ↑ „Annual Review of Astronomy and Astrophysics”. DOI: 10.1007/s00159-008-0012-y. Bibcode: 2008A&ARv..15..289T. (ang.).
- ↑ „Annual Review of Astronomy and Astrophysics”. DOI: 10.1146/annurev-astro-082708-101829. Bibcode: 2010ARA&A..48..673F. (ang.).
- ↑ George H. Jacoby. Planetary nebulae as standard candles. I – Evolutionary models. „Astrophysical Journal, Part 1 (ISSN 0004-637X)”. 339, s. 39–52, 1 kwietnia, 1989. DOI: 10.1086/167274. Bibcode: 1989ApJ...339...39J. (ang.).
- ↑ John L. Tonry, Alan Dressler, John P. Blakeslee, Edward A. Ajhar i inni. The SBF Survey of Galaxy Distances. IV. SBF Magnitudes, Colors, and Distances. „Astrophysical Journal”. 546 (2), s. 681–693, 2001. DOI: 10.1086/318301. Bibcode: 2001ApJ...546..681T. (ang.).
- ↑ Richard Powell, Michał Grochowiec (tłum.): 200 Najjaśniejszych Galaktyk. 2002-02-02. [dostęp 2013-06-28]. [zarchiwizowane z tego adresu (2012-08-18)].
- ↑ M. Bernardi, M.V. Alonso, L.N. da Costa, C.N.A. Willmer, G. Wegner, P.S. Pellegrini, C. Rité, M.A.G. Maia. Redshift-Distance Survey of Early-Type Galaxies. II. The Dn-σ Relation. „The Astronomical Journal”. 123 (5), s. 2159, 2005-05. DOI: 10.1086/339697. (ang.).
Linki zewnętrzne[edytuj | edytuj kod]
- Polskojęzyczne
![]() Nagrania na YouTube, kanał Astronarium [dostęp 2023-11-09]:
Nagrania na YouTube, kanał Astronarium [dostęp 2023-11-09]:
- Odległości we Wszechświecie, 7 lutego 2016.
- Kosmiczna drabina odległości, 4 kwietnia 2021.
- Anglojęzyczne
- The ABC’s of distances (UCLA)
- The Hubble Space Telescope Key Project on the Extragalactic Distance Scale
- NASA Cosmic Distance Scale
- PNLF information database. noao.edu. [zarchiwizowane z tego adresu (2010-01-26)].



























