Równoległość

Równoległość – w geometrii relacja między obiektami takimi jak proste, płaszczyzny, odcinki, półproste.

Aksjomaty

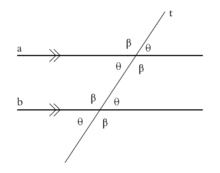
Aksjomat Euklidesa 

Jeżeli prosta (transwersalna) $t$ przecina proste $a, b$ tak, że kąty sobie odpowiadające są sobie różne, to proste $a, b$ przecinają się, co oznacza się $a \nparallel b$. Proste $a, b$, które są równoległe, opisuje się symbolem $a \parallel b$.

Szkocki matematyk John Playfair określił następujący aksjomat:

Aksjomat Playfaira 

Przez dowolny punkt można przeprowadzić prostą równoległą do zadanej prostej.

Geometria euklidesowa

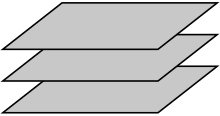
Geometrie euklidesowe to geometrie wykorzystujące aksjomat Euklidesa. Dwie proste na płaszczyźnie są równoległe, jeżeli nie przecinają się w żadnym punkcie lub mają ich nieskończenie wiele (pokrywają się).

Dwie płaszczyzny w przestrzeni trójwymiarowej są równoległe, jeśli nie mają punktów wspólnych lub pokrywają się.

Prosta i płaszczyzna w przestrzeni trójwymiarowej są do siebie równoległe, jeśli nie mają punktów wspólnych lub prosta leży na tej płaszczyźnie.

Analogicznie można definiować równoległość dla obiektów mających więcej wymiarów.

Własności

Ponieważ równoległość jest relacją równoważności, a więc jest

zwrotna: $a \parallel a$,

symetryczna: $a \parallel b$ pociąga $b \parallel a$,

przechodnia: $a \parallel b$ oraz $b \parallel c$, to $a \parallel c$,

Geometria analityczna

Proste równoległe zadane równaniem w postaci kierunkowej, mają równe współczynniki kierunkowe.

Dwie proste w przestrzeni kartezjańskiej są interpretacją graficzną układu dwóch równań liniowych z dwiema niewiadomymi. Proste równoległe odpowiadają układowi sprzecznemu (brak punktów wspólnych) lub zawsze spełnionemu (proste pokrywające się). Stąd dwie proste zadane równaniami ogólnymi

$\begin{cases} A_1x + B_1y + C_1 = 0 \\ A_2x + B_2y + C_2 = 0 \end{cases}$,

nie przecinają się lub pokrywają się, jeżeli wyznacznik (macierzy głównej) tego układu jest równy zeru:

$\begin{vmatrix} A_1 & B_1 \\ A_2 & B_2 \end{vmatrix} = 0 \iff A_1B_2 = A_2B_1$.

Odległość prostych równoległych

Odległość prostych równoległych - odległość któregokolwiek punktu leżącego na jednej prostej od jego rzutu prostopadłego na drugą prostą.

Niech l || k. Wówczas $l: Ax+By+C_1\,$ i $k: Ax+By+C_2\,$, gdy $A_2+B_2>0\,$. Odległość punktu O od prostej l wyraża się wzorem:

$d=\frac{|Ax_0+By_0+C_1|}{\sqrt{A^2+B^2}}$

Ponieważ O∈k $Ax_0+By_0+C_2=0\,$, więc $Ax_0+By_0= - C_2\,$.

Zatem wzór na odległość dwóch prostych równoległych ma postać:

$d=\frac{|C_1-C_2|}{\sqrt{A^2+B^2}}$

Jeżeli przedstawimy dane proste w postaci kierunkowej: $l: y=mx+n_1\,$, $k: y=mx+n_2\,$,

to wzór przybierze postać: $d=\frac{|n_1-n_2|}{\sqrt{1+m^2}}$

Geometrie nieeuklidesowe

Ta sekcja jest niekompletna. Jeśli możesz, rozbuduj ją.

W geometrii rzutowej każde dwie proste mają co najmniej jeden punkt przecięcia. Te o których geometria euklidesowa mówi, iż są równoległe (mają wspólny kierunek), w tej geometrii przecinają się w tzw. punkcie w nieskończoności.

W geometrii eliptycznej również każde dwie proste mają punkt wspólny, toteż pojęcie równoległości nie istnieje.

Zobacz też

• prostopadłość