Granica Roche’a





Granica Roche’a (czasem promień Roche’a) – promień sfery wokół cięższego ciała w układzie dwóch ciał o znacznej różnicy mas, po przekroczeniu którego ciało o mniejszej masie może się rozpaść pod wpływem sił pływowych[1], gdyż sama siła grawitacji nie jest w stanie utrzymać mniejszego ciała w całości[2]. Granica Roche’a wynosi od 2 do 3 promieni ciała o dużej masie. Promień nie jest jednoznacznie określony dla danego ciała centralnego, zależy też od właściwości satelity[3].
Pojęcie nazwano na cześć francuskiego astronoma Édouarda Roche’a, który pierwszy obliczył tę teoretyczną granicę w 1848[4].
Wstęp[edytuj | edytuj kod]
Siła oddziaływania grawitacyjnego zmienia się wraz z odległością od ciała będącego źródłem oddziaływania, odwrotnie proporcjonalnie do drugiej potęgi odległości między ciałami. Powoduje to, że zmiany siły są duże w małej odległości od ciała, a w dużej odległości pole grawitacyjne jest niemal jednorodne. W następstwie tego, jeśli satelita znajdzie się zbyt blisko swojego macierzystego ciała niebieskiego, różnica sił powstająca wewnątrz satelity na skutek niejednorodności pola grawitacyjnego może go rozerwać.
Promień Roche’a dotyczy danego układu dwóch ciał, i nie jest jednoznacznie określony dla masy ciała głównego. To samo ciało główne ma różną granicę dla różnych satelitów. Oprócz masy ciała, wokół którego rozpina się granica, zależy ona jeszcze od wielkości i masy satelity, a dokładniej od jego gęstości. Przy ustalonej wielkości satelity trudniej go rozerwać oraz zdeformować jego kształt, gdy jego siły grawitacyjne są większe, czyli gdy ma on większą masę (gęstość).
Niektóre satelity mogą poruszać się wewnątrz swoich granic Roche’a, ponieważ rozerwaniu przeciwdziałają siły inne niż grawitacyjne, na przykład naprężenia. Jednak w tej sytuacji każde niepowiązane z satelitą ciało leżące na jego powierzchni od strony ciała głównego lub naprzeciw, zostanie od niego oderwane. Księżyc Jowisza Metis oraz Saturna Pan są przykładami takich ciał[5].
Granicy Roche’a nie należy mylić ze spotykaną czasem strefą Roche’a (właściwa nazwa tej ostatniej to strefa Hilla).
Formuły określające granicę[edytuj | edytuj kod]
Zachowanie się satelity przybliżającego się do ciała o dużej masie zależy od sztywności satelity. W skrajnym przypadku, satelita jako całkowicie sztywne ciało, zbliżając się do granicy będzie utrzymywał swój pierwotny kształt, a po przekroczeniu granicy, zaczną z niego odpadać małe fragmenty, przybliżając się znaczniej może zostać nagle rozerwany. Z drugiej strony, ciało wyjątkowo płynne, przykładowo gazowe lub zawierające dużą atmosferę, będzie stopniowo zmieniało swój kształt, różnice w oddziaływaniu sił pływowych na jego rosnącej długości będą się zwiększać, a jego własne przyciąganie słabnąć, w końcu ciało centralne zacznie ssać gaz z satelity, dochodzi do akrecji.
Satelita sztywny[edytuj | edytuj kod]
Wyznaczając granicę Roche’a dla ciała sztywnego, zakłada się, że satelita pozostaje w całości dopóki ciało leżące na jego powierzchni nie zostanie porwane w górę przez siły pływowe ciała głównego. Dodatkowo, pomija się również inne cechy, takie jak nieregularny kształt (zakłada się kulistość), nierównomierny rozkład masy, obrót dookoła własnej osi oraz deformację ciała głównego. Te uproszczenia ułatwiają obliczenia.
Dla sztywnego sferycznego satelity, orbitującego wokół kulistego ciała, granica Roche’a, dana jest wzorem[6]:
gdzie jest promieniem ciała głównego, jest jego gęstością, jest gęstością satelity.
Gdy gęstość satelity jest dwa razy większa niż gęstość ciała głównego (na przykład skalisty księżyc wokół gazowej planety), granica Roche’a znajdzie się wewnątrz ciała głównego i nie będzie istotna.
Satelita płynny[edytuj | edytuj kod]
Satelita płynny pod wpływem sił pływowych zostaje rozciągnięty, tak jak to widać na ilustracjach, w wyniku czego materia z najbliższego oraz z najdalszego ciału głównemu miejsca satelity jest słabiej przyciągana przez satelitę i dlatego będzie z niego porywana, choć nie została przekroczona granica określona powyższym wzorem.
Wyznaczenie warunku oderwania z ciała płynnego jest trudne, ale po uproszczeniach pomijających niektóre efekty spłaszczenia ciała, dochodzi się do warunku jak dla ciała sztywnego, tyle że z innym stałym czynnikiem. Ten stały czynnik szacuje się numerycznie często z pomocą komputera.
W takiej formie wzór na granicę Roche’a podał autor pojęcia w 1848 (z minimalnie innym stałym czynnikiem – 2,44)[6].
Wyprowadzenie formuł[edytuj | edytuj kod]
Satelita sztywny[edytuj | edytuj kod]
Aby wyprowadzić zależność na granicę Roche’a, należy rozpatrzyć siły działające na ciało leżące na satelicie w punkcie najbliższym ciału głównemu (oznaczony jako ). Są to: siła ciągnąca ten fragment do reszty satelity oraz siła grawitacyjna ciągnąca go ku ciału głównemu – w tym przypadku jedynie siła pływowa, główna siła grawitacyjna jest równoważona przyspieszeniem uzyskiwanym przez satelitę.
Siłę przyciągającą ciało w stronę satelity (o promieniu masie ) wyraża prawem powszechnego ciążenia Newtona:
Siła pływowa działająca na masę w kierunku obiektu o dużej masie promieniu znajdującej się w odległości jest wyrażona jako:
Odległość ciał, w której obie siły równoważą się, jest uznawana za granicę Roche’a, zachodzi dla równości:
W tym szczególnym punkcie odległość między środkami ciał przechodzi właśnie w granicę Roche’a:
Zamieniając masy na gęstości:
Satelita płynny[edytuj | edytuj kod]
Wyprowadzając warunek oderwania ciała od płynnego satelity przyjmuje się, że satelita:
- w wyniku sił pływowych, zmienia kształt na podłużny, ale deformacja nie zmienia jego objętości,
- satelita obraca się z prędkością synchroniczną z obrotem wokół planety, będąc zwrócony cały czas tą samą stroną do ciała głównego.
Obrót synchroniczny oznacza, że płyn pozostaje nieruchomy, a problem można rozpatrywać jako statyczny w obracającym się wokół środka masy układzie współrzędnych. Dlatego też lepkość i tarcie wewnętrzne płynu nie grają tu roli, gdyż te czynniki miałyby znaczenie tylko w przypadku ruchów cieczy. Nie występuje też siła odśrodkowa wynikająca w obrotu satelity. Założenie o synchroniczności obrotów odpowiada większości przypadków rzeczywistych, gdyż gdy płynne ciało krążąc wokół centrum masy obraca się z prędkością inną niż prędkość synchroniczna, to siły pływowe doprowadzą obrót do prędkości synchronicznej.
Na płyn satelity oddziaływają zatem następujące siły:
- siła grawitacji ciała głównego,
- siła odśrodkowa w obracającym się układzie odniesienia,
- siła grawitacyjna satelity.
Ponieważ wszystkie te siły są zachowawcze (tzn. ich praca nie zależy od drogi), dlatego oddziaływania te mogą być reprezentowane za pomocą potencjału.
Powierzchnia satelity musi być powierzchnią stałego potencjału, gdyż inaczej istniałyby siły, powodujące ruch cieczy po powierzchni (a to wbrew założeniom). Należy zatem przedyskutować jaka forma powierzchni przy zadanej odległości od ciała głównego pozwala spełnić powyższy warunek stałego potencjału.

Siła grawitacyjna ciała głównego i siła odśrodkowa znoszą się wzajemnie na kołowej orbicie satelity, ale nie równoważą się poza nią, a ich różnica objawia się jako siły pływowe. Dla małych ciał odległość cząstki płynu od środka masy satelity jest mała w porównaniu z odległością od ciała głównego, a więc siła pływowa jest w przybliżeniu liniowa, a zatem może być wyrażona formułą opisującą powyżej.
W modelu satelity sztywnego znana jest odległość jego powierzchni od jego środka deformacja satelity płynnego zmusza do wyznaczenia deformacji.
Potencjał siły pływowej wyraża wzór:
Należy znaleźć kształt satelity, przy którym suma potencjału jego grawitacji i potencjału pływowego, na jego powierzchni jest stała. W ogólności problem tego typu jest bardzo trudny do rozwiązania. Ponieważ potencjał pływowy zmienia się tylko wzdłuż jednego kierunku (promienia wodzącego), można przyjąć, że siła pływowa deformuje kulistego satelitę wydłużając go w kierunku ciało główne – satelita, wobec tego przyjmuje się, że satelita ma kształt elipsoidy obrotowej. Dla elipsoidy potencjał na jego powierzchni może być wyrażony jako funkcja mimośrodu (spłaszczenia) tej elipsoidy:
gdzie jest potencjałem na najmniejszym promieniu („obrączce”), leżącym na płaszczyźnie symetrii elipsoidy gdzie Bezwymiarowa funkcja jest wyznaczana rozwiązania potencjału elipsoidy:
Wyrażenie to nie zależy od objętości satelity.
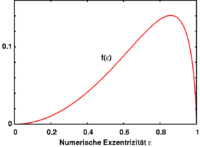
Zatem jakkolwiek skomplikowana byłaby zależność funkcji od mimośrodu elipsoidy wystarczy tylko dobrać odpowiednio wartość tak, aby potencjał był równy plus stała niezależna od zmiennej Jest tak dokładnie w przypadku, gdy
To równanie może być rozwiązane numerycznie. Z wykresu obok widać, że równanie to posiada dwa rozwiązania, a mniejsze z nich odpowiada spłaszczeniu (rozciągnięciu) satelity w równowadze stabilnej (tzn. elipsoidzie o mniejszym spłaszczeniu). To właśnie rozwiązanie wyznacza mimośród elipsoidy pływowej w zależności od ustalonej odległości od ciała głównego. Maksimum tej funkcji odpowiada największemu spłaszczeniu stabilnemu satelity. Argument funkcji, dla którego funkcja ma maksimum odpowiada, że pochodna funkcji ma miejsce zerowe. To miejsce odpowiada granicy Roche’a.

Maksymalne spłaszczenie elipsoidy pływowej można obliczyć numerycznie jako zero pochodnej funkcji
Odpowiada to stosunkowi osi 1:1,95. Wstawiając tę wartość do funkcji można obliczyć minimalną odległość, przy której elipsoida pływowa jeszcze istnieje – czyli granicę Roche’a:
Przykłady wartości granic Roche’a[edytuj | edytuj kod]
Poniższa tabela przedstawia średnie gęstości i promienie wybranych obiektów Układu Słonecznego.
| Obiekt | Gęstość (kg/m³) | promień (m) |
|---|---|---|
| Słońce | 1408 | 696 000 000 |
| Jowisz | 1326 | 71 492 000 |
| Ziemia | 5513 | 6 378 137 |
| Księżyc | 3346 | 1 738 100 |
| Saturn | 687,3 | 60 268 000 |
| Uran | 1318 | 25 559 000 |
| Neptun | 1638 | 24 764 000 |
Wykorzystując te dane można obliczyć granice Roche’a dla ciał sztywnych i płynnych. Tabela poniżej przedstawia wartości granic wyrażone w metrach i promieniach ciał głównych (średnia gęstość komet przyjmuje wartość około 500 kg/m³).
| Ciało | Satelita | Granica Roche’a (sztywna) | Granica Roche’a (płynna) | ||
|---|---|---|---|---|---|
| Odległość (km) | R | Odległość (km) | R | ||
| Ziemia | Księżyc | 9496 | 1,49 | 18 261 | 2,86 |
| Ziemia | typowa kometa | 17 880 | 2,80 | 34 390 | 5,39 |
| Słońce | Ziemia | 554 400 | 0,80 | 1 066 300 | 1,53 |
| Słońce | Jowisz | 890 700 | 1,28 | 1 713 000 | 2,46 |
| Słońce | Księżyc | 655 300 | 0,94 | 1 260 300 | 1,81 |
| Słońce | typowa kometa | 1 234 000 | 1,78 | 2 374 000 | 3,42 |
Jeśli gęstość ciała głównego jest ponad dwukrotnie mniejsza niż gęstość satelity, granica Roche’a dla ciała sztywnego jest mniejsza niż promień ciała głównego. W takim przypadku dwa obiekty mogą się zderzyć zanim granica zostanie osiągnięta.
Poniższa tabela pokazuje jak blisko swoich granic Roche’a (sztywnych i płynnych) znajdują się satelity Słońca (stosunek promieni ich orbit do wartości granic).
W rzeczywistości nie znamy gęstości większości wewnętrznych satelitów gazowych planet olbrzymów. W takich przypadkach (zaznaczone kursywą) przedstawione są wartości najbardziej prawdopodobne.
| Ciało główne | Satelita | Stosunek promienia orbity do granicy Roche’a | |
|---|---|---|---|
| (sztywna) | (płynna) | ||
| Słońce | Merkury | 104:1 | 54:1 |
| Ziemia | Księżyc | 41:1 | 21:1 |
| Mars | Fobos | 172% | 89% |
| Deimos | 451% | 234% | |
| Jowisz | Metis | ~186% | ~94% |
| Adrastea | ~188% | ~95% | |
| Amaltea | 175% | 88% | |
| Tebe | 254% | 128% | |
| Saturn | Pan | 142% | 70% |
| Atlas | 156% | 78% | |
| Prometeusz | 162% | 80% | |
| Pandora | 167% | 83% | |
| Epimeteusz | 200% | 99% | |
| Janus | 195% | 97% | |
| Uran | Kordelia | ~154% | ~79% |
| Ofelia | ~166% | ~86% | |
| Bianka | ~183% | ~94% | |
| Kresyda | ~191% | ~98% | |
| Desdemona | ~194% | ~100% | |
| Julia | ~199% | ~102% | |
| Neptun | Najada | ~139% | ~72% |
| Talassa | ~145% | ~75% | |
| Despoina | ~152% | ~78% | |
| Galatea | 153% | 79% | |
| Larissa | ~218% | ~113% | |
| Pluton | Charon | 12,5:1 | 6,5:1 |
Historyczne obserwacje[edytuj | edytuj kod]
Rozwiązanie dla ciał płynnych znajduje zastosowanie dla obiektów, których kształt nie jest sztywno utrzymywany przez grawitację, lub są kruche – na przykład komety. W 1992 r. kometa Shoemaker-Levy 9 przeszła przez swoją granicę Roche’a wokół Jowisza i rozpadła się na wiele mniejszych fragmentów. Dwa lata później, gdy przechodziła przez granicę ponownie, rozbiła się na planecie. Obserwacje orbity tej komety sugerują, że została ona przechwycona przez oddziaływanie grawitacyjne Jowisza już kilka dziesięcioleci przed jej ostatecznym rozbiciem[7].
Od dawna już sugeruje się też, że pierścienie Saturna powstały, gdy jeden (lub więcej) z jego księżyców wszedł za swoją granicę Roche’a wokół planety i został rozerwany przez siły pływowe. Z czasem nieregularnie ułożone bryły poddały się grawitacji Saturna i przybrały znaną nam dziś formę pierścieni. To rozwiązanie sugerował jeszcze sam Édouard Roche. Istnieją jednak alternatywne teorie dotyczące powstania pierścieni, między innymi przewidująca zderzenie księżyca planety z drugim, przypadkowym obiektem, na przykład kometą.
Znaczenie w tworzeniu ciał niebieskich[edytuj | edytuj kod]
Granica Roche’a pozwala prosto wytłumaczyć grawitacyjną niestabilność obłoków gazowo-pyłowych w pobliżu ciał w galaktykach, w pobliżu gwiazd i planet oraz tworzenie się ciał niebieskich z obłoków[8], a także tworzenie się ramion spiralnych w pyle krążącym wokół ciała centralnego[9].
Zobacz też[edytuj | edytuj kod]
Przypisy[edytuj | edytuj kod]
- ↑ granica Roche’a, [w:] Encyklopedia PWN [dostęp 2022-09-15].
- ↑ L. Czechowski, Planety widziane z bliska, Wiedza Powszechna 1985, Warszawa.
- ↑ Errol Hawkins: Secret History of Twin Planet Earth. Trafford Publishing, 2007, s. 115, 124. ISBN 978-1-4120-5567-3.
- ↑ What is the Roche limit?. NASA. [dostęp 2012-11-22]. [zarchiwizowane z tego adresu (2013-02-04)].
- ↑ Gunter Faure, Teresa M. Mensing: Introduction to Planetary Science: The Geological Perspective. Springer, 2007, s. 294. ISBN 978-1-4020-5544-7.
- ↑ a b Frank H. Shu: The Physical Universe: An Introduction to Astronomy. University Science Books, 1982, s. 431–433. ISBN 978-0-935702-05-7.
- ↑ International Planetarium Society Conference. seds.org. [zarchiwizowane z tego adresu (2009-02-13)]., Astronaut Memorial Planetarium & Observatory, Cocoa, Floryda. 1994.
- ↑ Hans Rickman: Collisional Processes in the Solar System. Springer, 2001. ISBN 978-0-7923-6946-2.
- ↑ Robin M. Canup, Kevin Righter: Origin of the Earth and Moon. University of Arizona Press, 2000. ISBN 978-0-8165-2073-2.
Bibliografia[edytuj | edytuj kod]
- Édouard Roche: La figure d’une masse fluide soumise à l’attraction d’un point éloigné, Acad. des sciences de Montpellier, Vol. 1 (1847-50) p. 243.


![{\displaystyle d=R\cdot {\sqrt[{3}]{2\;{\frac {\rho _{M}}{\rho _{m}}}}}\approx 1{,}25992\cdot R\cdot {\sqrt[{3}]{\frac {\rho _{M}}{\rho _{m}}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ded8a3f42dba2035e8a78a6342742947d9d4f0d)



![{\displaystyle d\approx 2{,}423\cdot R\cdot {\sqrt[{3}]{\frac {\rho _{M}}{\rho _{m}}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9969a49a29be39a5310459711f1365a66eab2abb)










![{\displaystyle d=r\cdot {\sqrt[{3}]{\frac {2M}{m}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2fc7d4e0522e92c8753173da08f74668fd338ed)
![{\displaystyle d=R\cdot {\sqrt[{3}]{2\;{\frac {\rho _{M}}{\rho _{m}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbe4c9ff76a2622ec4b9a92d787e8e83c25a1270)








![{\displaystyle f(\epsilon )={\frac {1-\epsilon ^{2}}{\epsilon ^{3}}}\cdot \left[\left(3-\epsilon ^{2}\right)\cdot \operatorname {arsinh} \left({\frac {\epsilon }{\sqrt {1-\epsilon ^{2}}}}\right)-3\epsilon \right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b8e8fd86da8cc3e3d3e9420ed8923db4a99869d)







![{\displaystyle d\approx 2{,}423\cdot R\cdot {\sqrt[{3}]{\frac {\rho _{M}}{\rho _{m}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d730239ed9e7b51bf0c3d948e7a5d2f07296dc6)