Praca (fizyka)
Praca – skalarna wielkość fizyczna, miara ilości energii przekazywanej między układami fizycznymi w procesach mechanicznych, elektrycznych, termodynamicznych i innych[1].
Praca w mechanice[edytuj | edytuj kod]
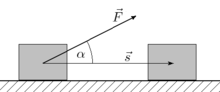
W ruchu postępowym[edytuj | edytuj kod]
Jeżeli ruch ciała jest prostoliniowy a wektor siły jest stały, pracę tej siły określa wzór
gdzie:
- – siła,
- – przemieszczenie (przesunięcie),
- – kąt między wektorem siły i przesunięcia.
W ogólnym przypadku, gdy wektor siły nie jest stały lub przemieszczenie nie jest prostoliniowe, praca jest sumą prac wykonanych na niewielkich odcinkach, na tyle małych, że spełnione są powyższe warunki. Wyraża ją wówczas wzór całkowy
gdzie:
- – praca,
- – całkowita droga, jaką pokonuje ciało[2],
- – siła,
- – wektor przesunięcia.
Jednostką miary pracy w układzie jednostek miar SI jest dżul (J) określany jako niuton·metr:
W ruchu obrotowym[edytuj | edytuj kod]
Praca wykonywana podczas obrotu ciała o kąt pod wpływem momentu sił wyraża się wzorem
Szczególne przypadki[edytuj | edytuj kod]
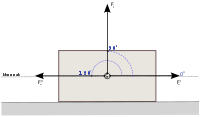
Dla szczególnych przypadków związanych z miarą kąta zawartego między siłą a przesunięciem jej punktu zaczepienia, wzór na pracę upraszcza się. Oto te przypadki:
- Gdy siła ma zwrot zgodny ze zwrotem przesunięcia jej punktu zaczepienia to kąt zawarty między siłą a przesunięciem jest równy 0°, a
- więc
- Gdy siła ma zwrot przeciwny do zwrotu wektora przesunięcia jej punktu zaczepienia, to kąt zawarty między siłą a przesunięciem jest równy 180°, a
- więc
- Gdy kierunek wektora siły jest prostopadły do kierunku wektora przesunięcia jej punktu zaczepienia, to kąt zawarty między siłą a przesunięciem jest równy 90°, a
- więc
Praca jest procesem przekazywania energii[3] i jest związana ze zmianą energii lub zamianą energii jednego rodzaju na energię innego rodzaju, np. praca niezrównoważonej siły grawitacji działającej na spadające ciało związana jest z zamianą energii potencjalnej (położenia) tego ciała na jego energię kinetyczną, a praca siły równoważącej siłę grawitacji podczas podnoszenia ciała zwiększa energię potencjalną (położenia). Związek między energią i pracą opisują niektóre sformułowania zasady zachowania energii.
Praca w termodynamice[edytuj | edytuj kod]
W termodynamice klasycznej praca równa jest energii, jaką układ termodynamiczny wymienia z otoczeniem przy zmianie swoich parametrów makroskopowych (objętość, położenie, natężenie pola itp.), jeżeli w otoczeniu wywołuje pracę rozumianą jako wielkość makroskopową, np. przesunięcie tłoka, przepływ prądu elektrycznego. Zmiana energii wewnętrznej układu niepowodująca wykonania pracy makroskopowej jest ciepłem (cieplnym przepływem energii)[2][4].
Przepływ energii będący pracą nie zmienia entropii układu, natomiast zmienia ją przepływ energii będący ciepłem. Skoro zmiana energii układu może wynikać zarówno z pracy, jak i z cieplnego przepływu energii, to ilość pracy nie jest jednoznacznie określona stanem początkowym i końcowym układu, lecz zależy od sposobu (drogi) przeprowadzenia procesu, dlatego praca jest funkcją procesu[4].
Z punktu widzenia termodynamiki statystycznej zmiana energii układu jest wynikiem oddziaływań cząstek biorących udział w danym procesie. Jeżeli ruchy cząstek wywołujące przepływ energii są uporządkowane, to z makroskopowego punktu widzenia, zmianę energii uznaje się pracę. Gdy natomiast są to ruchy nieuporządkowane, to związaną z nimi zmianę energii uznaje się za ciepło (cieplny przepływ energii)[4].
Praca objętościowa[edytuj | edytuj kod]
Praca w układzie termodynamicznym może się wiązać ze zmianą objętości układu, wówczas zwana jest pracą objętościową. Jeśli wykonaniu pracy nie towarzyszy zmiana objętości układu, mówimy o pracy nieobjętościowej. Przykładem pracy nieobjętościowej może być praca związana z przemieszczaniem ładunków w polu elektrycznym ogniwa paliwowego oraz ruch plazmy w polu magnetycznym w generatorze magnetohydrodynamicznym.
Zmiana objętości ciała znajdującego się pod działaniem sił zewnętrznych działających na jego powierzchnię lub umowną granicę wiąże się z wykonaniem pracy objętościowej. Pracę wykonaną przy niewielkiej zmianie objętości ciała, niewywołującej istotnej zmiany ciśnienia określają wzory:
gdzie:
- – praca wykonana na układzie ( – różniczka niezupełna),
- – ciśnienie zewnętrzne,
- – objętość układu.
Pojęcie pracy objętościowej jest używane także w hydrodynamice, termodynamice i wszystkich dziedzinach fizyki, w których rozpatruje się ciało znajdujące się pod wpływem zewnętrznego ciśnienia.
Zasadą określającą sposób wymiany energii z otoczeniem, w tym i przez pracę, jest pierwsza zasada termodynamiki.
Praca uogólniona[edytuj | edytuj kod]
W termodynamice uogólnieniem definicji pracy przyjętej w mechanice jest praca uogólniona. Wyrażenie na nieskończenie małą pracę (pracę elementarną) ma postać różniczki:
gdzie:
- xi – parametry zewnętrzne układu (zmienne ekstensywne),
- Xi – odpowiadające parametrom siły uogólnione (zmienne intensywne).
Parametry xi i Xi nazywane są zmiennymi sprzężonymi.
Jeżeli układ dokonuje przejścia między dwoma stanami, to praca układu jest równa sumie całek prac elementarnych. Całka ta zależy od sposobu przejścia między punktami. Oznacza to, że praca elementarna w ogólności nie jest różniczką zupełną względem współrzędnych xi, ale może być różniczką zupełną dla niektórych procesów (np. przemiany adiabatycznej izotermicznej gazu) i odpowiada zmianie potencjałów termodynamicznych (odpowiednio energii swobodnej, energii wewnętrznej)[2].
Co wyraża wzór:
Praca prądu elektrycznego[edytuj | edytuj kod]
Praca prądu elektrycznego jest sumą prac sił opisujących oddziaływanie poruszających się ładunków elektrycznych z siecią krystaliczną przewodnika (grzałki, żarówki itp.) lub z innymi poruszającymi się ładunkami wytwarzającymi pole magnetyczne (silniki prądu stałego).
Praca prądu elektrycznego w obwodzie prądu stałego jest równa iloczynowi napięcia źródła energii elektrycznej, natężenia prądu przepływającego przez odbiornik oraz czasu przepływu prądu. W przypadku zmian natężenia prądu lub napięcia praca jest sumą prac elementarnych podobnie jak w przypadku zmian siły.
Jednostką pracy w tym przypadku jest wolt·amper·sekunda równy dżulowi [J]
W skali makroskopowej, przy przepływie prądu elektrycznego przez rezystor, praca prądu zamieniana jest na ciepło. Przy przepływie prądu przez silnik elektryczny praca prądu zamieniana jest na pracę mechaniczną.
Przypisy[edytuj | edytuj kod]
- ↑ praca, [w:] Encyklopedia PWN [dostęp 2008-02-01].
- ↑ a b c „Encyklopedia fizyki” praca zbiorowa PWN 1973 t. 2 s. 842.
- ↑ Słownik fizyczny, Lech Jakubowski, Warszawa: Wiedza Powszechna, 1984, s. 307, ISBN 83-214-0053-1, OCLC 749487296.
- ↑ a b c Peter William Atkins: Chemia fizyczna. Warszawa: Wydawnictwo Naukowe PWN, 2001, s. 124. ISBN 83-01-13502-6.




























