Prawo powszechnego ciążenia
Prawo powszechnego ciążenia, zwane także prawem powszechnego ciążenia Newtona – prawo głoszące, że każdy obiekt we wszechświecie przyciąga każdy inny obiekt z siłą, która jest wprost proporcjonalna do iloczynu ich mas i odwrotnie proporcjonalna do kwadratu odległości między ich środkami[1]. Jest to ogólne prawo fizyczne, bazujące na empirycznych obserwacjach Newtona, które nazwał on indukcją (wpływem)[2]. Wchodzi ono w skład podstaw mechaniki klasycznej i zostało sformułowane w pracy Isaaca Newtona pt. Philosophiae naturalis principia mathematica, opublikowanej po raz pierwszy 5 lipca 1687 r. W języku współczesnym prawo to brzmi następująco[3]:
| Między dowolną parą ciał posiadających masy pojawia się siła przyciągająca, która działa na linii łączącej ich środki, a jej wartość jest wprost proporcjonalna do iloczynu ich mas i odwrotnie proporcjonalna do kwadratu odległości między ich środkami ciężkości. |
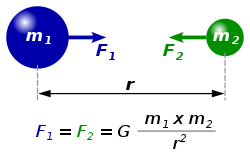

Matematycznie związek ten wyraża się wzorem:
gdzie:
- – stała grawitacji,
- – masa pierwszego ciała,
- – masa drugiego ciała,
- – długość wektora łączącego środki mas obu ciał,
- – wersor (wektor jednostkowy) osi łączącej środki mas obu ciał.
Siła jest wektorem, a jej wartość (długość tego wektora ) jest równa:
Stała grawitacji została uznana za jedną z podstawowych stałych fizycznych. Z pomiarów wynika, że jej wartość wynosi[4]:
Związek z prawami Keplera[edytuj | edytuj kod]
W swym dziele Newton przedstawił spójną teorię grawitacji, opisującą zarówno spadanie obiektów na ziemi, jak i ruch ciał niebieskich. Angielski fizyk oparł się na zaproponowanych przez siebie zasadach dynamiki oraz prawach Keplera dotyczących odległości planety od Słońca.
Dla uproszczenia załóżmy, że dwie planety poruszają się po kołowej orbicie. Prawo Keplera przyjmie dla nich postać:
(1) |
gdzie:
- – promienie orbit,
- – okresy obiegu planet.
Zgodnie z rachunkiem wektorowym ciało poruszające się po okręgu jest poddane przyspieszeniu:
gdzie: – przyspieszenie, – prędkość, – promień okręgu, co według II zasady dynamiki oznacza, że musi działać na nie siła dośrodkowa:
(2) |
gdzie to masa bezwładnościowa ciała.
Przy ruchu planet ta siła dośrodkowa jest równa sile grawitacyjnej Prędkość orbitalna może być wyliczona jako:
(3) |
Jeżeli podstawimy zależność (3) do (2) to otrzymamy:
Stosunek sił grawitacyjnych dla planet można rozpisać jako:
Jeżeli teraz do równania (4) podstawimy (1), to pozbędziemy się okresów obiegu:
Otrzymana zależność oznacza tyle, że stosunek sił grawitacyjnych jest proporcjonalny do odwrotności stosunku kwadratów odległości. Jeżeli planeta jest dwa razy dalej od Słońca, to siła grawitacji jest cztery razy mniejsza. Kiedy ciało ma dwa razy mniejszą masę, wtedy siła jest dwa razy mniejsza.
Newton uznał, że ta sama siła powoduje ruch planet po orbitach oraz spadanie jabłka z drzewa. W ten sposób ten wielki fizyk położył podwaliny pod mechanikę klasyczną. W tym ujęciu grawitacja jest siłą, z jaką oddziałują na siebie wszelkie ciała obdarzone masą.
Zasada równoważności[edytuj | edytuj kod]
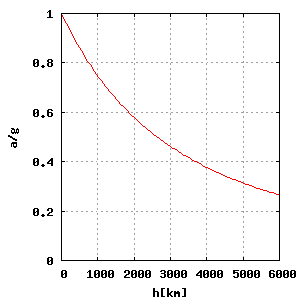
Masy grawitacyjne i nie muszą być równe masom bezwładnościowym występującym w II zasadzie dynamiki Newtona. Zaobserwowana równość tych wartości oznacza, że ruch ciała w polu grawitacyjnym nie zależy od jego masy. Postulat ten jako pierwszy wysunął Galileusz. Równoznaczność mas bezwładnościowych i grawitacyjnych, zupełnie przypadkowa z punktu widzenia mechaniki klasycznej, jest podstawą ogólnej teorii względności.
Równoważność masy bezwładnościowej i grawitacyjnej czekała na potwierdzenie eksperymentalne aż do roku 1798. Angielski fizyk Henry Cavendish jako pierwszy wykonał doświadczenia z wykorzystaniem oscylujących mas, dzięki którym określił wartość stałej grawitacyjnej z niepewnością 1%. W tym samym eksperymencie potwierdził też równoznaczność masy grawitacyjnej i bezwładnościowej.
Energia i potencjał[edytuj | edytuj kod]
Pole grawitacyjne jest polem potencjalnym. Praca wykonywana w tym polu nie zależy od drogi, po jakiej przemieszczają się ciała, tylko od różnicy potencjałów w punkcie początkowym i końcowym. Możliwe jest zatem zdefiniowanie funkcji która opisuje potencjał pola grawitacyjnego. Spełnia ona następującą zależność:
Korzystając z tego równania, można obliczyć energię potencjalną pola grawitacyjnego.
Zobacz też[edytuj | edytuj kod]
Przypisy[edytuj | edytuj kod]
- ↑ Newtona prawo ciążenia, [w:] Encyklopedia PWN [dostęp 2021-08-07].
- ↑ Isaac Newton: In [experimental] philosophy particular propositions are inferred from the phenomena and afterwards rendered general by induction, w: Principia, Book 3, General Scholium, s. 392, Volume 2 of Andrew Motte’s English translation published 1729.
- ↑ Proposition 75, Theorem 35, s. 956 – I. Bernard Cohen and Anne Whitman, translators: Isaac Newton, The Principia: Philosophiae naturalis principia mathematica. Preceded by A Guide to Newton’s Principia, by I. Bernard Cohen. University of California Press 1999 ISBN 0-520-08816-6 ISBN 0-520-08817-4.
- ↑ CODATA Value 2018: Newtonian constant of gravitation. [dostęp 2022-03-30]. (ang.).
Linki zewnętrzne[edytuj | edytuj kod]
- Witold Sadowski, Prawo powszechnego ciążenia, [w:] pismo „Delta”, deltami.edu.pl, grudzień 2023, ISSN 0137-3005 [dostęp 2023-12-09] (pol.).































