Teoria strun
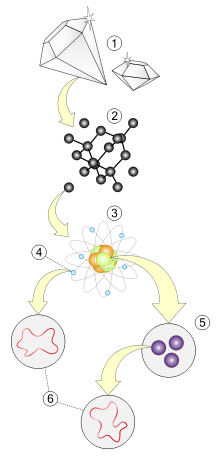
1. Makroskopowy
2. Molekularny
3. Atomowy
4. Subatomowy – elektrony
5. Subatomowy – kwarki
6. Strunowy

Teoria strun (TS) – koncepcja w fizyce teoretycznej, zgodnie z którą:
- podstawowym (fundamentalnym) budulcem materii nie są punktowe cząstki, lecz rozciągłe struny[1] o wielkości ok. 10−31 metra;
- czasoprzestrzeń ma co najmniej 10 wymiarów. Oprócz czterech wymiarów makroskopowych, otwartych – trzech przestrzennych oraz czasu – teorie strun przewidują co najmniej sześć dodatkowych wymiarów przestrzeni. Mają one być niedostępne codziennemu doświadczeniu ani dotychczasowym eksperymentom za sprawą kompaktyfikacji – zwinięcia do skrajnie małych rozmiarów, sięgających skali Plancka wyznaczającej granice stosowalności znanej fizyki.
Model ten może prowadzić do wielkiej unifikacji oddziaływań cząstek – zjawiska elektrosłabe i jądrowe silne mogą się w nim połączyć w jedno, poszukiwane oddziaływanie elektrojądrowe. Oprócz tego teorie strun uwzględniają grawitację, co czyni je możliwymi teoriami superunifikacji. Czasem modele tego typu są zwane teoriami wszystkiego przez opisywanie wszystkich znanych oddziaływań podstawowych (elektrosłabego, jądrowego silnego oraz ciążenia).
Teoria strun zaczęła powstawać na przełomie lat 60. i 70. XX wieku, głównie dzięki pracom Gabriele Veneziano, Leonarda Susskinda i Yoichiro Nambu, początkowo jako teoria oddziaływań jądrowych[2]. Ogłoszona w 1970 roku bozonowa teoria strun zawierała ponad 20 dodatkowych wymiarów i nie opisywała wszystkich cząstek elementarnych – pomijała fermiony. Jednak dzięki wprowadzeniu supersymetrii stworzono teorie superstrun – opisujące wszystkie znane cząstki i redukujące liczbę dodatkowych wymiarów do sześciu, co daje czasoprzestrzeń 10-wymiarową[3]. Powstało pięć różnych modeli superstrunowych, a w latach 90. okazało się, że istnieją między nimi związki nazywane dualnościami. Stąd wysunięto przypuszczenie, że wszystkich pięć teorii superstrun to różne aspekty jednej teorii wyższego rzędu: M-teorii zaproponowanej przez Edwarda Wittena. Wprowadzony przez nią jedenasty wymiar czasoprzestrzeni – czyli siódmy wymiar dodatkowy – nie tylko pozwolił połączyć całą piątkę teorii superstrun, ale włączył także do nich 11-wymiarową supergrawitację. To powiązanie sześciu modeli nazwano drugą rewolucją strunową[4][a]. Następnie pod koniec lat 90. Juan Maldacena wykazał korespondencję AdS/CFT, dowodząc że pewne warianty teorii strun spełniają zasadę holograficzną[5]. W XXI wieku część badaczy zaczęła rozważać koncepcję krajobrazu strunowego będącego formą Wieloświata[6].
Teoria strun wywołała mieszane opinie wśród fizyków. Od początku spotykała się z krytyką[potrzebny przypis], jednak zaangażowała co najmniej setki naukowców[7], w tym wybitnych jak nobliści, m.in. David Gross (nobel 2004) i Yoichiro Nambu (nobel 2008). Teoretyków strun zatrudniono w najlepszych na świecie ośrodkach fizyki teoretycznej jak Institute for Advanced Study (IAS) w Princeton, a ich postępy doceniono zaszczytami jak medale. Przez pewien czas była jedynym obiecującym modelem kwantowej grawitacji[1], a w 2022 roku pozostaje prawdopodobnie jedyną potencjalną teorią wszystkich oddziaływań[potrzebny przypis]. Zastosowano ją do kosmologii i fizyki materii skondensowanej; była też popularyzowana przez szereg autorów, najpóźniej od lat 80.
Z drugiej strony dekady starań nie rozwiązały podstawowych trudności teorii strun, przede wszystkim ograniczonych perspektyw na dowody doświadczalne. Te i inne problemy – a także rosnąca konkurencja ze strony innych modeli – nasiliły krytykę. Padała ona ze strony zróżnicowanych fizyków, reprezentujących różne specjalności, pokolenia, ośrodki i poglądy, a w gronie sceptyków znaleźli się też fizycy najwybitniejsi jak nobliści. Kontrowersje wokół strun przyczyniły się do dyskusji na temat problemu demarkacji w filozofii nauki – kwestionowano poprawność metodologiczną tego projektu badawczego i naukowość jego niektórych elementów jak Wieloświat[potrzebny przypis].
Wstęp[edytuj | edytuj kod]
Teoria strun zakłada, że elektrony i kwarki wewnątrz atomu nie są 0-wymiarowymi obiektami, lecz 1-wymiarowymi strunami. Struny te mogą oscylować, nadając obserwowanym cząstkom ich zapach, ładunek, masę i spin. Pomiędzy trybami oscylacji strun istnieje bezmasowy stan o spinie 2 – grawiton. Istnienie stanu grawitonu oraz fakt, że równania opisujące teorię strun zawierają równania OTW Einsteina, oznacza, że teoria strun jest kwantową teorią grawitacji. Ponieważ TS (teoria strun) jest matematycznie spójna, to wielu uważa, że w pełni opisuje nasz wszechświat, co czyni ją teorią wszystkiego. TS zawiera konfiguracje, które opisują wszystkie obserwowane, fundamentalne siły, lecz ze stałą kosmologiczną równą 0 i z pewnymi nowymi polami[8]. Inne konfiguracje zawierają inne wartości stałej kosmologicznej oraz są metastabilne, lecz długowieczne. To prowadzi niektórych naukowców do założeń, że istnieje przynajmniej jedno metastabilne rozwiązanie jakościowo identyczne z modelem standardowym, z niezerową stałą kosmologiczną, zawierające ciemną materię oraz możliwy mechanizm dla istnienia kosmicznej inflacji. Nie jest obecnie wiadome, czy TS posiada takie rozwiązanie lub jak bardzo jest elastyczna, aby dopuścić odpowiedni dobór szczegółów.
TS zawiera także inne obiekty, tzw. brany. Słowo brana pochodzi od membrany i odnosi się do odmiany wewnętrznie powiązanych obiektów takich jak D-brany, czarne p-brany czy 5-brany Neveu-Schwarza. Są to rozszerzone obiekty będące źródłami dla uogólnień form różniczkowych wektora potencjału pola elektromagnetycznego. Obiekty te są ze sobą powiązane przez różne odmiany dualności. Czarne dziury jak p-brany są identyfikowane z D-branami, które są końcowymi punktami dla strun, oraz to utożsamienie nazywane jest dualnością cechowania i grawitacji. Badania nad tą zamiennością doprowadziły do nowego spojrzenia na kwantową chromodynamikę, podstawową teorię silnego oddziaływania jądrowego[9][10][11][12]. Struny tworzą zamknięte pętle, chyba że napotkają D-brany, gdzie mogą być otwarte w postaci 1-wymiarowych linii. Punkty końcowe nie mogą przerwać D-bran, lecz mogą ślizgać się na nich.
Pełna teoria nie posiada satysfakcjonującej definicji we wszystkich okolicznościach, ponieważ rozpraszanie strun jest najbardziej bezpośrednio zdefiniowane przez teorię perturbacji. Kompletna mechanika kwantowa wysoko wymiarowych bran nie jest łatwo zdefiniowana, a zachowanie TS w kosmologii (czasowo zależnym środowisku) nie jest w pełni opracowane. Nie jest także jasne, czy istnieje jakaś zasada, dzięki której TS wybiera swoje stany próżniowe, konfiguracji czasoprzestrzeni, która określa właściwości naszego wszechświata.
Podstawowe właściwości[edytuj | edytuj kod]
Teorię strun (TS) można sformułować w terminologii zasady działania (akcji) albo Nambu-Goto, albo Polakowa, co opisuje, jak struny propagują przez przestrzeń i czas. W przypadku nieobecności zewnętrznych interakcji, dynamika strun jest rządzona przez napięcia oraz energię kinetyczną, które razem powodują oscylacje. Mechanika kwantowa strun pokazuje, że te oscylacje istnieją w dyskretnych wibracyjnych trybach, widma emisyjnego teorii.
W odległościach większych niż promień struny każdy tryb oscylacji zachowuje się jak inny gatunek cząstki z ich masą, spinem i ładunkiem określonym przez dynamikę struny. Podział oraz rekombinacja strun korespondujących do emisji cząstki oraz absorpcji daje podstawy do interakcji między cząstkami. Analogią dla trybów wibracji struny jest struna gitary odtwarzająca wiele różnych muzycznych nut. Jedyną różnicą jest fakt, że struna gitary istnieje w 3-wymiarowej przestrzeni, więc istnieją tylko dwa wymiary poprzeczne do struny. Struny podstawowe istnieją w przestrzeni 9-wymiarowej, dzięki czemu struny mogą wibrować w dowolnym kierunku, co oznacza, że spektrum trybów wibracji jest wiele bogatsze.
TS zawiera oba typy strun otwarte, które mają dwa odległe punkty końcowe, i zamknięte, tworzące pętlę. Te dwa typy strun zachowują się w nieco odmienny sposób. Dla przykładu we wszystkich TS dla grawitonu trybem struny jest struna zamknięta[13], lecz tylko struny otwarte mogą wibrować jak fotony. Ponieważ dwa końce otwartej struny mogą zawsze się spotkać i połączyć, formując zamkniętą strunę, nie istnieją teorie strun bez strun zamkniętych.
Najwcześniejszy model struny, struna bozonowa, zawierała tylko bozonowe stopnie swobody. Model ten opisuje, w wystarczająco niskich energiach, teorię kwantowej grawitacji, która także zawiera (jeżeli struny otwarte są rozważane) pola cechowania takie jak foton (lub ogólniej każdą teorię cechowania). Jednakże model ten ma problemy. Teoria ta posiada fundamentalną niestabilność będącą wynikiem rozpadu samej czasoprzestrzeni. W dodatku jak sama nazwa wskazuje, spektrum cząstek zawiera tylko bozony – cząstki, które jak fotony podlegają szczególnym zasadom zachowania. Bozony są składnikami promieniowania, lecz nie materii, która jest zbudowana z fermionów. Badanie, jak TS może zawierać fermiony, prowadzi do wprowadzenia supersymetrii, matematycznej relacji między bozonami i fermionami. TS, które zawierają fermionowe wibracje, są obecnie znane jako teorie superstrun; kilka rodzajów było opisanych, lecz wszystkie są uważane za granice M-teorii.
Pewne jakościowe właściwości strun kwantowych mogą być rozumiane jako dosyć prosty styl. Dla przykładu struny kwantowe mają napięcie takie jak zwykłe struny zrobione z dratwy; to napięcie jest uważane za podstawowy parametr teorii. Napięcie struny kwantowej jest blisko związane do jej rozmiaru. Rozważmy zamkniętą pętlę strunową, na którą nie działają żadne siły zewnętrzne, mogącą się poruszać swobodnie w przestrzeni. Jej napięcie dąży do skurczenia jej w coraz to mniejszą pętlę. Intuicja wynikająca z klasycznej mechaniki sugeruje, że może to spowodować skurczenie się jej do punktu, ale taki scenariusz naruszyłby zasadę nieoznaczoności Heisenberga. Charakterystyczny rozmiar pętli strunowej będzie przeciwwagą między siłą napięcia, dążącą do skurczenia jej, a rezultatem zasady nieoznaczoności, co utrzymuje ją rozciągniętą. Konsekwencją tego jest minimalny rozmiar struny związany z jej napięciem.
Powierzchnia świata[edytuj | edytuj kod]

Ruch punktowej cząstki można opisać wykresem pozycji (w jedno lub dwuwymiarowej przestrzeni) względem czasu. Powstający w rezultacie obraz przedstawia linię świata cząstki (jej historię) w czasoprzestrzeni. Analogicznie można otrzymać podobny wykres przedstawiający strunę z upływem czasu. Struna (jednowymiarowy obiekt) przebiega powierzchnię (dwuwymiarową rozmaitość), znaną jako powierzchnia świata (worldsheet). Różne tryby (modulacje) strun (reprezentujące cząstki takie jak fotony czy grawitony) są falami na powierzchni tej rozmaitości.
Zamknięte struny wyglądają jak małe pętle, więc ich powierzchnie świata będą wyglądały jak rury lub, w ogólnej terminologii, Powierzchnia Riemanna (dwuwymiarowa orientowana rozmaitość) bez brzegów (bez krawędzi). Otwarta struna wygląda jak krótka linia, więc jej powierzchnia świata będzie wyglądać jak pasek lub inaczej powierzchnia Riemanna z brzegiem.
Struny mogą się dzielić i łączyć. Ten stan jest odzwierciedlony przez formę ich powierzchni świata (topologię). Na przykład, jeżeli zamknięta struna się podzieli, to jej powierzchnia świata będzie wyglądała jak pojedyncza rura podzielona (lub połączona) do dwóch rur (częstym odnośnikiem jest para spodni — rysunek obok). Jeżeli zamknięta struna podzieli się, a następnie jej dwie części ponownie się połączą, to jej powierzchnia świata będzie wyglądała jak pojedyncza rura podzielona na dwa, następnie połączona, co również wygląda jak torus połączony do dwóch rur (jedna reprezentuje wchodzącą strunę a druga wychodzącą). Otwarta struna zachowująca się tak samo będzie miała swoją powierzchnię świata wyglądającą jak pierścień połączony do dwóch pasków.
Na uwagę zasługuje fakt, że proces łączenia i podziału strun jest procesem globalnym powierzchni świata, nie lokalnym: lokalnie powierzchnia świata wygląda tak samo wszędzie i nie jest możliwe wskazanie pojedynczego punktu na powierzchni, gdzie podział się pojawia. Zatem te procesy są integralną częścią teorii i są opisane tą samą dynamiką, która kontroluje tryby (modulacje) strun.
W pewnych TS (zamkniętych strunach typu I oraz pewnych wersjach strun bozonowych), struny mogą się podzielić oraz połączyć w przeciwnej orientacji (jak we wstędze Möbiusa lub butelce Kleina). Teorie te nazywają się niezorientowane. W terminologii formalnej powierzchnia świata w tych teoriach jest nieorientowaną powierzchnią.
Dualności[edytuj | edytuj kod]
Przed latami 90. XX wieku teoretycy zakładali, że istnieje pięć odrębnych teorii superstrun: otwarta typu I, zamknięta typu I, zamknięta typu IIA, zamknięta typu IIB i dwa zapachy heterotycznej teorii strun (SO(32) i E8xE8)[14]. Rozumowano, że tylko jedna z tych pięciu kandydatek będzie właściwą teorią wszystkiego i że to będzie ta, której limit niskiej energii, w dziesięciu wymiarach przestrzennych skompaktyfikowanych w dół do czterech będzie odpowiadał obserwowanym wielkościom fizycznym. Obecnie już wiadomo, że ten obraz był niepoprawny oraz że pięć teorii superstrun jest połączone wzajemnie w taki sposób, jak gdyby każda z nich była specjalnym przypadkiem jakiejś bardziej fundamentalnej (podstawowej) teorii (M-teorii). Te teorie są związane przez transformacje, które nazywane są dualnościami. Jeżeli dwie teorie są związane przez transformację dualną, to oznacza, że pierwsza teoria może być transformowana w pewien sposób, że skończy wyglądając zupełnie jak druga teoria. Mówi się wtedy, że te dwie teorie są dualne względem siebie, zakładając określoną transformację. Ujmując w inny sposób, można stwierdzić, że dwie teorie są różnym matematycznym opisem tego samego zjawiska.
Te dualności łączą wielkości, które uważano za odrębne. W dużych i małych skalach wielkości, jak i w silnych i słabych oddziaływaniach, istnieją wielkości takie, które zawsze oznaczały bardzo odległe granice zachowania systemu fizycznego zarówno w klasycznej teorii pola, jak i w kwantowej fizyce cząstek elementarnych. T-dualizm odnosi duże i małe skale odległości między teoriami strun, S-dualizm odnosi się do silnego i słabego sprzężenia sił między teoriami strun. U-dualizm łączy T-dualizm i S-dualizm.
| Typ | Wymiary czasoprzestrzenne | Szczegóły |
|---|---|---|
| Bozonowa | 26 | Tylko bozony, brak fermionów, opisuje tylko siły, brak opisu materii, oba typy strun otwarte i zamknięte; główna wada: cząstki z urojoną masą (tachiony), reprezentują niestabilności w teorii |
| I | 10 | Supersymetria między siłami i materią, oba typy strun zamknięte i otwarte; brak tachionów; symetria grup SO(32) |
| IIA | 10 | Supersymetria między siłami i materią, tylko struny otwarte połączone z D-branami; brak tachionów; bezmasowe fermiony są niechiralne |
| IIB | 10 | Supersymetria między siłami i materią, tylko struny otwarte połączone z D-branami; brak tachionów; bezmasowe fermiony są chiralne |
| HO | 10 | Supersymetria między siłami i materią, tylko struny otwarte połączone z D-branami; brak tachionów; heterotyczna, oznacza różnicę między prawo i lewoskrętnymi strunami; symetria grup SO(32) |
| HE | 10 | Supersymetria między siłami i materią, tylko struny zamknięte; brak tachionów; heterotyczna; symetria grup E8xE8 |
Należy zauważyć, że w teoriach strun typu IIA i IIB dopuszczalne jest, aby zamknięte struny poruszały się wszędzie przez dziesięciowymiarową czasoprzestrzeń, podczas gdy otwarte struny mają ich końce przytwierdzone do D-bran, które są membranami niższej wymiarowości (ich wymiary są nieparzyste — 1, 3, 5, 7 lub 9 — w typie IIA i parzyste — 0, 2, 4, 6 lub 8 — w typie IIB, włącznie z kierunkiem czasu).
Dodatkowe wymiary[edytuj | edytuj kod]
Liczba wymiarów[edytuj | edytuj kod]
Ciekawą właściwością TS jest fakt, że przewiduje ona dodatkowe wymiary. W klasycznej TS liczba wymiarów nie jest ustalona żadnym logicznym kryterium. Jednakże, aby uczynić ją zgodną z teorią kwantową, wymaga się od TS, aby istniała w czasoprzestrzeni o tzw. krytycznym wymiarze: odpowiednio dla teorii strun bozonowych jest to 26 wymiarów czasoprzestrzennych i 10 dla teorii superstrun. To jest koniecznością dla zapewnienia zanikania anomalii konforemnej powierzchni świata konforemnej teorii pola. Nowoczesne rozumienie sugeruje, że istnieją mniej trywialne drogi spełnienia tego kryterium. Rozwiązania kosmologiczne istnieją w szerszej różnorodności wymiarowości i te inne wymiary są powiązane przez dynamiczne przejścia[15][16].
Jedną z takich teorii jest 11-wymiarowa M-teoria, która wymaga czasoprzestrzeni o jedenastu wymiarach[17], w przeciwieństwie do zwykłych trzech wymiarów przestrzennych i czwartego wymiaru czasu. Oryginalne teorie strun z lat 80. XX wieku opisują specjalne przypadki M-teorii, gdzie jedenasty wymiar jest bardzo małym okręgiem lub linią oraz jeżeli te sformułowania są rozważane jako fundamentalne, wtedy teoria strun wymaga dziesięciu wymiarów. Lecz TS opisuje także wszechświaty takie jak nasz z czterema dającymi się zaobserwować wymiarami, jak i wszechświaty nawet z 10 płaskimi wymiarami przestrzennymi i także nie pokazuje, gdzie pozycja w niektórych wymiarach jest opisana liczbą zespoloną zamiast liczbą rzeczywistą. Pojęcie wymiaru czasoprzestrzennego nie jest stałe w TS: najlepiej pomyśleć o tym jako różne w zależności od okoliczności[18].
Nic w teorii elektromagnetyzmu Maxwella lub teorii względności Einsteina nie przewiduje niczego takiego. Teorie te wymagają od fizyków podania liczby wymiarów manualnie i arbitralnie i liczba ta jest stała, niezależna od energii potencjalnej. TS dopuszcza powiązanie liczby wymiarów ze skalarem potencjalnej energii. W terminologii technicznej dzieje się tak, ponieważ anomalia cechowania istnieje dla każdego przewidywanego wymiaru przestrzennego oddzielnie, anomalii cechowania można przeciwdziałać przez dołączenie nietrywialnej energii potencjalnej do równań, aby rozwiązać równania ruchu. Dalej nieobecność energii potencjalnej w "krytycznym wymiarze" wyjaśnia, dlaczego rozwiązania dla płaskiej czasoprzestrzeni są możliwe.
Najlepiej zrozumieć to, gdy foton zawarty w spójnej teorii (technicznie, cząstka niosąca siłę powiązaną do niezłamanej symetrii cechowania) musi być bezmasowa. Masa fotonu, która jest przewidziana przez TS, zależy od energii trybu struny reprezentującej foton. Energia ta zawiera udział z efektu Casimira, mianowicie z fluktuacji kwantowych w strunie. Rozmiar tego wkładu zależy od liczby wymiarów, ponieważ dla większej liczby wymiarów istnieje więcej możliwych fluktuacji w pozycji struny, wskutek czego foton w płaskiej czasoprzestrzeni będzie bezmasowy – a teoria spójna – tylko dla szczególnej liczby wymiarów[b]. Kiedy wykona się niezbędne kalkulacje, to krytyczna wymiarowość nie jest cztero- (jak można by się spodziewać 3 wymiary przestrzenne plus jeden czasowy). Podzbiór X jest równy relacji fluktuacjom fotonu w liniowym wymiarze. Przestrzenno płaskie TS są 26-wymiarowe w przypadku bozonowym, podczas gdy teorie superstrun i M-teorii zawierają 10 lub 11 wymiarów dla rozwiązań płaskich. W bozonowych teoriach 26 wymiarów pochodzi z równań Polakowa. Wychodząc od dowolnego wymiaru większego od 4, jest konieczne rozważenie, jak są one zredukowane do czterowymiarowej czasoprzestrzeni.
Wymiary kompaktowe[edytuj | edytuj kod]

Aby rozwiązać ww. problem, zaproponowano dwa wyjścia. Pierwsze to kompaktyfikacja dodatkowej liczby wymiarów; w szczególności 6 lub 7 dodatkowych wymiarów są tak małe, że nie można ich wykryć przy obecnym stanie technicznych możliwości.
Aby zachować wysoki stopień supersymetrii, te skompaktyfikowane przestrzenie muszą być bardzo specjalne, aby znalazły odzwierciedlenie w swojej holonomii. 6-wymiarowa rozmaitość musi posiadać strukturę SU(3), szczególnym przypadkiem jest (nieskręcona) holonomia SU(3), co czyni ją przestrzenią Calabiego-Yau, a 7-wymiarowa rozmaitość musi posiadać strukturę rozmaitości G2, z holonomią G2 będącą znów specyficznym, prostym przypadkiem. Takie przestrzenie były badane przy próbach powiązania TS z 4-wymiarowym Modelem Standardowym, po części z powodu prostoty obliczeniowej wynikającej z założenia supersymetrii.
Standardową analogią przy rozważaniu wielowymiarowych przestrzeni jest wąż ogrodowy. Jeżeli wąż jest oglądany z odpowiedniej odległości, to wygląda, jakby był jednowymiarowy — posiadał tylko długość. Jeżeli pomyśli się o kuli o rozmiarze pozwalającym na wrzucenie jej do środka węża, to będzie się ona poruszała, w przybliżeniu, w jednym wymiarze; w jakimkolwiek eksperymencie jedynym ważnym ruchem będzie ruch jednowymiarowy. Jednak jeżeli zbliży się do węża, to zauważy się, że posiada on obwód. Wtedy mrówka krocząca po wewnętrznej ścianie węża będzie się poruszać w dwóch wymiarach (a mucha latająca we wnętrzu w trzech). Te dodatkowe wymiary są widoczne jedynie z relatywnie bliskiej odległości, lub eksperymentując z cząstkami z ekstremalnie małymi długościami fal (rzędu wielkości promienia wymiaru kompaktowego), co w mechanice kwantowej oznacza bardzo wysokie energie (dualizm korpuskularno-falowy).
Scenariusz świata Bran[edytuj | edytuj kod]
Inną możliwością jest przypuszczenie, że utknęliśmy w 3+1 wymiarowej podprzestrzeni pełnego wszechświata. Odpowiednio zlokalizowana materia i pola cechowania Yanga-Millsa będą istniały, jeżeli podprzestrzeń jest wyjątkowym zbiorem większego wszechświata[19]. Te "wyjątkowe zbiory" są wszechobecne w n-fałdach Calabiego-Yau i mogą być opisane jako podprzestrzenie bez lokalnych deformacji, pokrewnych do zmarszczek na kawałku papieru lub rysy na krysztale, których otoczenie jest znacząco inne od wyjątkowej samej podprzestrzeni. Jednakże do chwili pojawienia się pracy Randall i Sundruma[20], nie było wiadome, że grawitacja może być poprawnie zlokalizowana w pod-czasoprzestrzeni. W dodatku czasoprzestrzeń może być warstwowa, zawierająca warstwy różnych wymiarów, dopuszczająca, abyśmy zamieszkiwali 3+1 wymiarową warstwę — takie geometrie pojawiają się naturalnie w kompaktyfikacjach Calabiego-Yau[21]. Takie pod-czasoprzestrzenie są D-branami, w związku z tym modele takie znane są jako scenariusze świata bran.
Skutki istnienia ukrytych wymiarów[edytuj | edytuj kod]
W każdym przypadku grawitacja działająca w ukrytych wymiarach wpływa na inne niegrawitacyjne siły takie jak elektromagnetyzm. I rzeczywiście wczesne prace Kaluzy pokazują, że ogólna teoria względności w pięciu wymiarach przewiduje istnienie elektromagnetyzmu. Jednakże z uwagi na właściwości rozmaitości Calabiego-Yau nie pojawiają się żadne nowe siły pochodzące z małych wymiarów, ale ich kształt ma głęboki wpływ na to, jak siły między strunami pojawiają się w naszym czterowymiarowym wszechświecie. W zasadzie jest możliwa dedukcja natury tych dodatkowych wymiarów wymagając zgodności z modelem standardowym, lecz obecnie nie istnieje taka praktyczna możliwość. Możliwe jest także wydobycie informacji odnośnie do ukrytych wymiarów przez precyzyjne testy grawitacji.
D-brany[edytuj | edytuj kod]
Inną kluczową właściwością TS jest istnienie D-bran. Są to membrany o innej wymiarowości (począwszy od zero wymiarowej membrany — która jest w rzeczywistości punktem — przez 2-wymiarowe membrany, 3-wymiarowe wielkości itd.)
D-brany są zdefiniowane przez fakt, że granice powierzchni świata są do nich przyczepione. D-brany posiadają masę, ponieważ emitują i absorbują zamknięte struny, co opisuje grawitony i w — teoriach superstrun — także ładunek, ponieważ łączą się z otwartymi strunami, to opisuje także interakcje cechowania.
Z punktu widzenia otwartych strun D-brany są obiektami, do których ich końce są przyczepione. Struny otwarte przyczepione do D-brany określa się jako "żyjące" na niej i dają początek teoriom cechowania "żyjącym" na nich (ponieważ jedna z trybów modeli otwartych strun jest bozonem cechowania, jak foton). W przypadku D-bran istnieje jeden typ bozonu cechowania i otrzymujemy abelową teorię cechowania (z fotonem jako bozonem cechowania). Jeżeli istnieje wiele równoległych D-bran, to będzie istniało wiele typów bozonów cechowania dając początek nieabelowej teorii cechowania.
D-brany są grawitacyjnymi źródłami, na których teoria cechowania "żyje". Ta teoria cechowania jest połączona z grawitacją, co oznacza, że każdy z tych dwóch punktów widzenia jest niekompletny.
Eksperymentalna weryfikowalność[edytuj | edytuj kod]
Kilka głównych trudności komplikuje wysiłki skierowane na przetestowanie teorii. Najbardziej znaczącą jest ekstremalnie mały rozmiar długości Plancka, a oczekuje się, że struny w TS są bliskie tej długości. Teoretyczna możliwość przetestowania teorii istnieje, zatem jest falsyfikowalna w sensie popperowskim.
Inną kwestią jest olbrzymia liczba metastabilnych próżni teorii strun, które mogą być efektywnie zróżnicowane, aby pomieścić prawie każdy fenomen obserwowany w niższych energiach.
Prognozy[edytuj | edytuj kod]
Harmonika strun[edytuj | edytuj kod]
Jedną unikatową prognozą teorii strun jest istnienie harmoniki strun: w wystarczająco wysokich energiach strunowy charakter cząstek powinien być oczywisty. Powinny tu istnieć cięższe kopie wszystkich cząstek korespondujących do wyższej harmoniki wibracyjnej struny. Nie jest jasne, jak wysokie te energie są. W najbardziej konwencjonalnych modelach strunowych nie byłyby dużo niższe od energii Plancka, około 1014 razy wyższej niż energie dostępne w najnowszych akceleratorach cząstek elementarnych, co czyni te prognozy niemożliwe do przetestowania w jakimkolwiek akceleratorze w niedalekiej przyszłości. Jednakże w modelach z dużymi dodatkowymi wymiarami mogą być wyprodukowane w LHC lub w energiach niewiele wyższych od niego.
Kosmologia[edytuj | edytuj kod]
Współczesne rozumienie teorii strun podsuwa kilka prognoz dla struktury wszechświata w największych skalach. Wiele faz w TS ma bardzo dużą, pozytywną energię próżni[22]. Regiony wszechświata znajdujące się w takiej fazie podlegałyby wykładniczemu wzrostowi inflacji w procesie znanym jako wieczna inflacja. Zgodnie z przewidywaniami tej teorii większość wszechświata gwałtownie się rozszerza. Jednakże te fazy ekspansji nie są stabilne i mogą się rozpaść przez powstające zarodki baniek o niższej energii próżni. Ponieważ nasz lokalny region wszechświata nie rozszerza się w sposób gwałtowny, TS przewiduje, że istniejemy właśnie w takiej bańce. Przestrzenna Krzywizna naszego "wszechświata" wewnątrz baniek, które zostały uformowane w tym procesie, jest negatywna, co jest prognozą możliwą do przetestowania[23]. Idąc dalej, inne bańki ewentualnie uformują się w próżni, którą można nazwać rodzicem, na zewnątrz i będą mogły się z nią zderzać. Kolizje te prowadzą do potencjalnie obserwowalnych śladów w kosmologii[24][25]. Jednakże, jest także możliwe, że nic z ww. rzeczy nie zostanie zaobserwowane, jeżeli przestrzenna krzywizna jest zbyt mała oraz kolizje są zbyt rzadkie.
Kosmiczne struny[edytuj | edytuj kod]
W niektórych okolicznościach fundamentalne struny powstające w momencie lub pod koniec inflacji mogą być "rozciągnięte" do astronomicznych wielkości. Te kosmiczne struny mogą być zaobserwowane na kilka sposobów, np. poprzez ich efekt soczewkowania grawitacyjnego. Jednak niektóre teorie pola także przewidują powstanie kosmicznych strun z topologicznych defektów w konfiguracji pola[26].
Siła grawitacji[edytuj | edytuj kod]
Teorie z dodatkowymi wymiarami przewidują, że siła grawitacji zwiększa się bardziej gwałtownie na małych dystansach niż w przypadku 3 wymiarów (gdzie zwiększa się jak r-2). Zależnie od rozmiaru wymiarów, to może prowadzić do zjawiska takiego jak produkcja mikro czarnych dziur w LHC lub może zostać wykryte w eksperymentach mikrograwitacyjnych.
Chromodynamika kwantowa[edytuj | edytuj kod]
TS była oryginalnie zaproponowana jako teoria hadronów, a jej analiza doprowadziła do nowego spojrzenia na chromodynamikę kwantową – teorię cechowania, która jest fundamentalną teorią opisującą Oddziaływanie silne.
Matematyczna technika z TS (korespondencja AdS/CFT) została użyta do opisu ilościowych cech zachowania plazmy kwarkowo-gluonowej w relatywistycznych zderzeniach ciężkich jonów[27][28][29][30].
Supersymetria[edytuj | edytuj kod]
Jeżeli potwierdzona eksperymentalnie, supersymetria może być także rozważana jako dowód za TS, ponieważ została odkryta w kontekście TS i wszystkie spójne TS są supersymetryczne. Jednakże nieobecność supersymetrycznych cząstek w energiach dostępnych dla LHC nie będzie dowodem na jej nieaktualność, ponieważ skala energii, w której supersymetria jest złamana, może być poza zasięgiem akceleratora.
Centralnym problemem dla zastosowania jest najlepsze zrozumienie podstaw, że TS zachowuje znacznie z supersymetrii jako z bazowej teorii, której rezultatem są czasowo niezmiennicze przestrzenie. Obecnie TS nie może sobie poradzić czasową zależnością, kosmologicznym tłem. Jednak zaproponowano kilka modeli, aby prognozować złamanie supersymetrii, najbardziej znaczącym jest model KKLT[22], wprowadzający brany i fluksy, aby uczynić kompaktyfikację metastabilną.
Korespondencja AdS/CFT[edytuj | edytuj kod]
AdS/CFT odnosi TS do teorii cechowania i dopuszcza kontakt z eksperymentami niskich energii w kwantowej chromodynamice. Ten typ TS, który opisuje tylko silne interakcje, jest znacznie mniej kontrowersyjny dzisiaj niż teorie strun wszystkiego[31].
Sprzężenie stałej unifikacji[edytuj | edytuj kod]
Wielka unifikacja jest naturalna w teoriach strun wszystkiego i wymaga, aby sprzężone stałe czterech oddziaływań spotkały się w jednym punkcie przy reskalowaniu grup renormalizacji. Jest to także falsyfikowalne stwierdzenie, ale nie ogranicza się do TS, lecz także jest wspólne dla teorii wielkiej unifikacji[32].
Dualizm Cechowania/grawitacji[edytuj | edytuj kod]
Dualizm Cechowania/grawitacji jest przypuszczalną dualnością między kwantową teorią grawitacji w niektórych przypadkach i teorią cechowania w mniejszej liczbie wymiarów. Oznacza to, że każde przewidywane zjawisko i wielkość w jednej teorii ma analogię w drugiej teorii ze "słownikową" możliwością tłumaczenia z jednej na drugą.
Opis dualizmu[edytuj | edytuj kod]
W niektórych przypadkach teoria cechowania na D-branach jest odłączona od grawitacji będącej w wiązce; jednak otwarte struny przyczepione do D-bran nie wchodzą w interakcje z zamkniętymi strunami.
W tych przypadkach D-brany mają dwa niezależne, alternatywne opisy. Jak wspomniane wyżej z punktu widzenia zamkniętych strun, D-brany są grawitacyjnymi źródłami, więc mamy grawitacyjną teorię na czasoprzestrzeni z pewnymi polami tła. Z punktu widzenia otwartych strun, fizyka D-bran jest opisana przez odpowiednią teorię cechowania. W takich przypadkach często przypuszcza się, że teoria grawitacyjna na czasoprzestrzeni z odpowiednimi polami tła jest dualna (fizycznie zamienna) do teorii cechowania na granicy tej czasoprzestrzeni (ponieważ podprzestrzeń wypełniona przez D-brany jest granicą tej przestrzeni). Ta dualność nie została dowiedziona w żadnym przypadku, więc nie ma zgodności między teoretykami co do kwestii jak silnie dualizm działa na poszczególne modele.
Przykłady i intuicja[edytuj | edytuj kod]
Najlepszym znanym przykładem jest dualizm między superstruną Typu IIB na AdS5 x S5 (przestrzeń produktów pięciowymiarowej przestrzeni Anty de Sittera i pięć-sfery) z jednej strony oraz N= 4 supersymetryczną teorią Yanga-Millsa na czterowymiarowej granicy przestrzeni Anty de Sittera (płaska czterowymiarowa czasoprzestrzeń R3,1 lub trój-sfera z czasem S3 x R). Co jest znane jako Korespondencja AdS/CFT[33][34][35][36], nazwa często używana dla dualności cechowania/grawitacji. Dwa dodatkowe przykłady zawierają M-teorię na AdS4 x S7, opisane przez ABJM superkonforemną teorię pola w 2+1 wymiarach[37] i M-teorię na AdS7 x S4, opisaną przez tzw. (2,0)-teorię w 5+1 wymiarach[38]. Prognozuje się, że druga teoria istnieje przez klasyfikacje superkonforemnych teorii pól[39], lecz nie jest znany jej lagranżjan, jednakże ten sam opis zastosowany był dla teorii ABJM, zanim znaleziono jej lagranżjan[40].
Ten dualizm można sobie wyobrazić w następujący sposób: rozważmy czasoprzestrzeń ze źródłem grawitacji, np. Ekstremalna czarna dziura[41]. Gdy cząstki są daleko od tego źródła, to są opisane przez zamknięte struny (teoria grawitacji lub supergrawitacji). Gdy cząstki zbliżają się do źródła grawitacji, to nadal mogą być opisane przez zamknięte struny; także mogą być opisane przez obiekty podobne do strun występujących w kwantowej chromodynamice[42][43][44], które są zbudowane z bozonów cechowania (gluonów) i innych stopni swobody teorii cechowania[45]. Jeżeli więc ktoś jest w stanie opisać system grawitacyjny jako dwa oddzielne regiony — jeden odległy od źródła i inny bliski źródła — wtedy ten drugi region może także być opisany przez teorię cechowania D-bran. Ten drugi region (bliski źródła) jest określany jako limit bliski horyzontu, ponieważ zwykle istnieje horyzont zdarzeń wokół źródła grawitacji.
W teorii grawitacji jednym z kierunków w czasoprzestrzeni jest kierunek radialny, oddalający się od źródła grawitacyjnego. Teoria cechowania żyje tylko na samej D-branie, więc nie zawiera kierunku radialnego: żyje na czasoprzestrzeni z mniejszym o jeden wymiarem w porównaniu do teorii grawitacji.
Fizyka teorii grawitacyjnej bliskiej horyzontowi zawiera tylko stany na powłoce masy (przeważnie w ST), podczas gdy teoria pola zawiera także funkcje korelacji poza powłoką masy. Stany na powłoce w bliskiej horyzontowi teorii grawitacji mogą być pomyślane jako opisujące tylko cząstki pochodzące z wiązki do regionu bliskiego horyzontowi i podlegające tam wzajemnym interakcjom. W teorii cechowania są to "projekcje" na granicę, więc cząstki przybywające do źródła z różnych kierunków będą widziane w teorii cechowania jako (poza powłoką) kwantowe fluktuacje wzajemnie odległe, gdy cząstki przybywające do źródła z prawie tych samych kierunków w przestrzeni będą widziane w symetrii cechowania jako (poza powłoką) fluktuacje kwantowe bliskie wzajemnie. Kąt między przybywającymi cząstkami w teorii grawitacji tłumaczy się na odległość skali między kwantowymi fluktuacjami w teorii cechowania. Kąt między przybywającymi cząstkami w teorii grawitacji jest związany z radialną odległością od źródła grawitacji, na którym cząstki podlegają interakcji: im większy kąt, tym bliżej cząstki mają, aby dostać się do źródła i aby zaszła między nimi interakcja. Z drugiej strony skala odległości między fluktuacjami kwantowymi w kwantowej teorii pola jest powiązana (odwrotnie) do skali energii w tej teorii, więc mały promień w teorii grawitacji tłumaczy się na niską skalę energii w teorii cechowania i odwrotnie.
Prosty przykład: jeżeli w teorii grawitacji istnieje konfiguracja, w której pole dylatonu jest malejące wraz z promieniem, wtedy dualna teoria pola będzie asymptotycznie swobodna (sprzężenie będzie rosło słabiej w wysokich energiach).
Nagrody za badania strun[edytuj | edytuj kod]

Rozwój teorii strun został wyróżniony co najmniej kilkunastoma nagrodami naukowymi, nie tylko z fizyki. Do 2022 roku przyznano za to:
- kilka Nagród Sakurai, wiodących w teorii cząstek[c];
- najwyższe nagrody w fizyce teoretycznej ogółem i fizyce matematycznej jak:
- Medal Lorentza[d];
- Medal Diraca (ICTP)[e];
- Medal Diraca (IOP)[f];
- Dannie Heineman Prize for Mathematical Physics[g];
- nagrody dla fizyków wszelkich dyscyplin, ustępujące głównie Nagrodzie Nobla w dziedzinie fizyki jak:
- Nagroda Fizyki Fundamentalnej (ang. Breakthrough Prize)[h];
- Medal Newtona[i];
- wyróżnienia matematyczne – Witten otrzymał Medal Fieldsa (1990), Nagrodę Nemmersa w dziedzinie matematyki (2000), Nagrodę Crafoorda w dziedzinie matematyki (2008) i Nagrodę Kioto w dziedzinie matematyki (2014);
- nagrody obejmujące różne nauki:
- brytyjski Royal Medal[j];
- amerykański National Medal of Science[k];
- międzynarodowa Albert Einstein World Award of Science[l].
W 2002 roku teoretyk strun Michio Kaku założył się z dziennikarzem Johnem Horganem o tysiąc dolarów, że do 2020 roku teoria strun lub inna teoria unifikacyjna będzie nagrodzona Nagrodą Nobla. Kaku przegrał zakład[46].
Krytyka i obrona[edytuj | edytuj kod]
Sceptycy[edytuj | edytuj kod]
Teoria strun do tej pory (2022) nie ma dowodów na swą słuszność. Część fizyków zarzucała jej nikłe perspektywy potwierdzenia i problemy teoretyczne. Wśród krytyków znaleźli się nobliści w dziedzinie fizyki, związani z różnymi obszarami badań:
- Philip Anderson, teoretyk materii skondensowanej zahaczający również o teorię cząstek, noblista z 1977 roku. Stwierdził, że teoria strun jest „pierwszą od setek lat nauką, która uprawiana jest w sposób przed-baconowski, bez żadnej odpowiedniej procedury eksperymentalnej”[47].
- Sheldon Lee Glashow, teoretyk cząstek (nobel 1979). Stwierdził ironicznie, że teoria ta jest „absolutnie bezpieczna”, jako że nie ma żadnego sposobu, by ją zweryfikować i ewentualnie obalić[48].
- Steven Weinberg, teoretyk cząstek i kosmolog (nobel 1979). Stracił nadzieje pokładane w tej teorii, mimo pewnej otwartości na odważne spekulacje jak Wieloświat[49].
- Roger Penrose, teoretyk względności i grawitacji (relatywista) oraz matematyk (nobel 2020). Nie neguje TS jako nauki[50] ani nie kwestionuje tego, że podstawowym budulcem materii może być struna, a nie punkt. Mimo to odrzuca dodatkowe wymiary czasoprzestrzeni[51].
Inni krytycy to:
- Peter Woit, teoretyk cząstek i matematyk z Uniwersytetu Columbia. W 2004 roku otworzył bloga Not Even Wrong poświęconego krytyce teorii strun[52]. W 2006 roku opublikował książkę o tym samym tytule; stara się w niej udowodnić nie tyle fałszywość tej teorii, co jej absurdalność[53]. Książkę tę skrytykował teoretyk strun Luboš Motl, zarzucający Woitowi niewiedzę[54]. Mimo to po przeszło dekadzie Woit podtrzymał swoje krytyczne opinie i czuł się w nich utwierdzony[55][56], a w 2022 roku dalej prowadził swojego bloga;
- Lee Smolin, relatywista, zajmujący się między innymi kwantowaniem grawitacji; w 2006 roku również opublikował książkę krytyczną wobec teorii strun[57][58];
- George Ellis, wpływowy relatywista oraz filozof nauki[59];
- Sabine Hossenfelder, relatywistka, także pracująca nad kwantowaniem grawitacji. Krytykuje supersymetrię[60], nie widząc dobrych powodów do unifikacji oddziaływań ani żadnej innej rewizji modelu standardowego cząstek elementarnych[potrzebny przypis].
Powstały też konkurencyjne teorie i prototypy kwantowej grawitacji jak pętlowa grawitacja kwantowa (ang. LQG) oraz modele oparte na geometrii nieprzemiennej.
Reakcja na krytykę[edytuj | edytuj kod]
Na zarzuty Woita i Smolina odpowiedział między innymi astrofizyk teoretyczny Sean M. Carroll. W 2006 roku stwierdził, że[potrzebny przypis]:
- silna pozycja akademicka teorii strun jest uzasadniona merytorycznie;
- zarzuty braku dowodów są niecierpliwe;
- różnorodność kierunków badań nie powinna być sztucznie zwiększana;
- konkurencyjne modele nie wytworzyły niczego równie obiecującego.
Carroll podkreślał ciągłe postępy teoretyczne strun, m.in. dużą rolę korespondencji AdS/CFT w zrozumieniu kwantowych teorii pola[61]. Rok później powiedział, że „teoria strun nie jest jeszcze martwa”[62].
Status i perspektywy teorii strun były też publicznie dyskutowane w 2007 roku przez Briana Greene i astrofizyka Lawrence’a Kraussa, broniącego pozycji sceptyka. Prowadzący humorystyczną dyskusję astrofizyk Michael Turner nie wskazał wyraźnego zwycięzcy[63]. Napięcia między fizykami wywołane teorią strun zostały też przedstawione w popkulturze, w serialu Teoria wielkiego podrywu (ang. The Big Bang Theory)[64].
Zobacz też[edytuj | edytuj kod]
Uwagi[edytuj | edytuj kod]
- ↑ Pierwsza nastąpiła w latach 80., kiedy Witten usunął z istniejących wtedy teorii strun osobliwości, przywracając ten model do głównego nurtu badań[potrzebny przypis].
- ↑ Obliczenie liczby wymiarów można obejść przez dodanie stopnia swobody, który skompensuje "brakujące" fluktuacje kwantowe. Jednak ten stopień swobody zachowuje się podobnie do wymiaru czasoprzestrzennego jedynie w pewnych aspektach, a otrzymana teoria nie jest zgodna z Lorentzowską niezmienniczością i posiada inne właściwości, które nie są obecne w naturze.
- ↑ Nagrody Sakurai za wkład w teorie strun otrzymali m.in. Leonard Susskind (1998), Lisa Randall (2019) i Nima Arkani-Hamed (2022).
- ↑ Witten (2010) i Maldacena (2018).
- ↑ Witten (1985), Maldacena (2008) i Veneziano (2014).
- ↑ Michael Green (2004) i Michael Duff (2017).
- ↑ Witten (1998), Veneziano (2004) oraz Maldacena i Polchinski (2007).
- ↑ Arkani-Hamed, Maldacena i Witten (2012) oraz Polchinski (2017).
- ↑ Witten (2010).
- ↑ Michael Green (2021), zob.
 Michael Green, strona Towarzystwa Królewskiego w Londynie, royalsociety.org [dostęp 2022-01-11].
Michael Green, strona Towarzystwa Królewskiego w Londynie, royalsociety.org [dostęp 2022-01-11].
- ↑ Witten (2002).
- ↑ Witten (2016).
Przypisy[edytuj | edytuj kod]
- ↑ a b Strun teoria, [w:] Encyklopedia PWN [dostęp 2021-09-15].
- ↑
 Leonard Susskind, Why is Quantum Gravity Key?, (ang.), 0:40, kanał Closer to Truth na YouTube, 14 czerwca 2020 [dostęp 2022-01-12].
Leonard Susskind, Why is Quantum Gravity Key?, (ang.), 0:40, kanał Closer to Truth na YouTube, 14 czerwca 2020 [dostęp 2022-01-12].
- ↑
 Piotr Sułkowski, 1+2+3+… = -1/12, zapytajfizyka.fuw.edu.pl, 23 maja 2015 [dostęp 2022-01-12]
Piotr Sułkowski, 1+2+3+… = -1/12, zapytajfizyka.fuw.edu.pl, 23 maja 2015 [dostęp 2022-01-12]
- ↑
 Sean M. Carroll, A Bit of Physics History: Ed Witten Introduces M-Theory, (ang.) preposterousuniverce.com [dostęp 2022-01-13].
Sean M. Carroll, A Bit of Physics History: Ed Witten Introduces M-Theory, (ang.) preposterousuniverce.com [dostęp 2022-01-13].
- ↑
 Piotr Sułkowski, Czym jest hipoteza holografii?, zapytajfizyka.fuw.edu.pl, 2 lutego 2018 [dostęp 2022-01-12].
Piotr Sułkowski, Czym jest hipoteza holografii?, zapytajfizyka.fuw.edu.pl, 2 lutego 2018 [dostęp 2022-01-12].
- ↑
 Łukasz Lamża, Krajobraz teorii strun, kanał Centrum Kopernika Badań Interdyscyplinarnych, 15 maja 2019 [dostęp 2023-05-21].
Łukasz Lamża, Krajobraz teorii strun, kanał Centrum Kopernika Badań Interdyscyplinarnych, 15 maja 2019 [dostęp 2023-05-21].
- ↑ string theory, [w:] Encyclopædia Britannica [dostęp 2023-06-22] (ang.). (...) hundreds of researchers had dropped what they were working on and turned their full attention to string theory.
- ↑ Burt A. Ovrut (2006). "A Heterotic Standard Model". Fortschritte der Physik 54-(2–3): 160–164.
- ↑ H. Nastase, More on the RHIC fireball and dual black holes, BROWN-HET-1466, arXiv:hep-th/0603176, Marzec 2006.
- ↑ Liu, Hong; Rajagopal, Krishna; Wiedemann, Urs (2007). "Anti–de Sitter/Conformal-Field-Theory Calculation of Screening in a Hot Wind". Physical Review Letters 98 (18). arXiv:hep-ph/0607062.
- ↑ Liu, Hong; Rajagopal, Krishna; Wiedemann, Urs Achim (2006). "Calculating the Jet Quenching Parameter". Physical Review Letters 97 (18). arXiv:hep-ph/0605178
- ↑ H. Nastase, The RHIC fireball as a dual black hole, BROWN-HET-1439, arXiv:hep-th/0501068, Styczeń 2005.
- ↑
 Piotr Sułkowski, W jaki sposób teoria grup łączy się z teorią strun?, zapytajfizyka.fuw.edu.pl, 24 stycznia 2021 [dostęp 2022-01-12].
Piotr Sułkowski, W jaki sposób teoria grup łączy się z teorią strun?, zapytajfizyka.fuw.edu.pl, 24 stycznia 2021 [dostęp 2022-01-12].
- ↑ S. James Gates, Jr., Ph.D., Superstring Theory: The DNA of Reality "Lecture 23 – Can I Have That Extra Dimension in the Window?"
- ↑ Hellerman, Simeon; Swanson, Ian (2007). "Dimension-changing exact solutions of string theory". Journal of High Energy Physics 2007 (9): 096. arXiv:hep-th/0612051v3
- ↑ Aharony, Ofer; Silverstein, Eva (2007). "Supercritical stability, transitions, and (pseudo)tachyons". Physical Review D 75 (4). arXiv:hep-th/0612031v2
- ↑ M. J. Duff, James T. Liu and R. Minasian Eleven Dimensional Origin of String/String Duality: A One Loop Test Center for Theoretical Physics, Department of Physics, Texas A&M University.
- ↑ Polchinski, Joseph (1998). String Theory, Cambridge University Press ISBN 0-521-67229-5.
- ↑ Zobacz dla przykładu: T. Hübsch, "A Hitchhiker’s Guide to Superstring Jump Gates and Other Worlds", in Proc. SUSY 96 Conference, R. Mohapatra and A. Rasin (eds.), Nucl. Phys. (Proc. Supl.) 52A (1997) 347–351.
- ↑ Randall, Lisa (1999). "An Alternative to Compactification". Physical Review Letters 83 (23): 4690. arXiv:hep-th/9906064.
- ↑ Aspinwall, Paul S.; Greene, Brian R.; Morrison, David R. (1994). "Calabi-Yau moduli space, mirror manifolds and spacetime topology change in string theory". Nuclear Physics B 416 (2): 414. arXiv:hep-th/9309097.
- ↑ a b Kachru, Shamit; Kallosh, Renata; Linde, Andrei; Trivedi, Sandip (2003). "De Sitter vacua in string theory". Physical Review D 68 (4). arXiv:hep-th/0301240.
- ↑ Freivogel, Ben; Kleban, Matthew; Martínez, María Rodríguez; Susskind, Leonard (2006). "Observational consequences of a landscape". Journal of High Energy Physics 2006 (3): 039. arXiv:hep-th/0505232.
- ↑ M. Kleban, T. Levi, and K. Sigurdson, Observing the landscape with cosmic wakes, arXiv:1109.3473.
- ↑ S. Nadis, "How we could see another universe,", June 2009. Astronomy.com. Retrieved on 2012-07-11.
- ↑ Polchinski, Joseph. "Introduction to Cosmic F- and D-Strings". arXiv:hep-th/0412244.
- ↑ H. Nastase, More on the RHIC fireball and dual black holes, BROWN-HET-1466, arXiv:hep-th/0603176, marzec 2006.
- ↑ Liu, Hong; Rajagopal, Krishna; Wiedemann, Urs (2007). "Anti–de Sitter/Conformal-Field-Theory Calculation of Screening in a Hot Wind". Physical Review Letters 98 (18). arXiv:hep-ph/0607062.
- ↑ Liu, Hong; Rajagopal, Krishna; Wiedemann, Urs Achim (2006). "Calculating the Jet Quenching Parameter". Physical Review Letters 97 (18). arXiv:hep-ph/0605178.
- ↑ H. Nastase, The RHIC fireball as a dual black hole, BROWN-HET-1439, arXiv:hep-th/0501068, Styczeń 2005.
- ↑ S. James Gates, Jr., Ph.D., Superstring Theory: The DNA of Reality "Lecture 21 – Can 4D Forces (without Gravity) Love Strings?", 0:26:06-0:26:21, cf. 0:24:05-0:26-24.
- ↑ Idem, "Lecture 19 – Do-See-Do and Swing your Superpartner Part II" 0:16:05-0:24:29.
- ↑ J. Maldacena, The Large N Limit of Superconformal Field Theories and Supergravity, arXiv:hep-th/9711200.
- ↑ S. S. Gubser, I. R. Klebanov and A. M. Polyakov (1998). "Gauge theory correlators from non-critical string theory". Physics Letters B428: 105–114. arXiv:hep-th/9802109.
- ↑ Edward Witten (1998). "Anti-de Sitter space and holography". Advances in Theoretical and Mathematical Physics 2: 253–291. arXiv:hep-th/9802150.
- ↑ Aharony, O.; S.S. Gubser, J. Maldacena, H. Ooguri, Y. Oz (2000). "Large N Field Theories, String Theory and Gravity". Phys. Rept. 323 (3–4): 183–386. arXiv:hep-th/9905111.
- ↑ N=6 superconformal Chern-Simons-matter theories, M2-branes and their gravity duals.
- ↑ ntLab: 6d (2,0)-supersymmetric QFT.
- ↑ Restrictions Imposed by Superconformal Invariance on Quantum Field Theorie.
- ↑ John Schwarz Dirac Memorial Lecture on superconformal field theories
- ↑ Dijkgraaf, Robbert; Verlinde, Erik; Verlinde, Herman (1997). "5D black holes and matrix strings". Nuclear Physics B 506: 121. arXiv:hep-th/9704018v2.
- ↑ Eto, Minoru; Hashimoto, Koji; Terashima, Seiji (2007). "QCD string as vortex string in Seiberg-dual theory". Journal of High Energy Physics 2007 (9): 036. arXiv:0706.2005v1.
- ↑ Meyer, Harvey B. (2005). "Vortices on the worldsheet of the QCD string". Nuclear Physics B 724: 432. arXiv:hep-th/0506034v1.
- ↑ Koji Hashimoto (2007) Cosmic Strings, QCD Strings and D-branes
- ↑ Piljin Yi (2007) "Story of baryons in a gravity dual of QCD"
- ↑ John Horgan, String Theory Does Not Win a Nobel, and I Win a Bet, Scientific American, blogs.scientificamerican.com, 8 października 2019 [dostęp 2022-01-14].
- ↑
 What do you believe is true even though you cannot prove it? (ang.), edge.org, 2005 [dostęp 2022-01-11].
What do you believe is true even though you cannot prove it? (ang.), edge.org, 2005 [dostęp 2022-01-11].
- ↑
 Sheldon Glashow, Viewpoints on String Theory (ang.), wywiad dla portalu „Nova. The Elegant Universe”, pbs.org, lipiec 2003 [dostęp 2022-01-11].
Sheldon Glashow, Viewpoints on String Theory (ang.), wywiad dla portalu „Nova. The Elegant Universe”, pbs.org, lipiec 2003 [dostęp 2022-01-11].
- ↑
 John Horgan, Nobel Laureate Steven Weinberg Still Dreams of Final Theory, Scientific American, blogs.scientificamerican.com, 1 maja 2015 [dostęp 2022-01-11].
John Horgan, Nobel Laureate Steven Weinberg Still Dreams of Final Theory, Scientific American, blogs.scientificamerican.com, 1 maja 2015 [dostęp 2022-01-11].
- ↑ Sir Roger Penrose: Fashion, Faith, and Fantasy in the New Physics of the Universe[1], [dostęp 05.02.2017]
- ↑ Podkast rozmowy z Rogerem Penrosem. sciencefriday.com. [zarchiwizowane z tego adresu (2014-06-03)]. z 4 kwietnia 2014
- ↑
 Introduction, math.columbia.edu, 17 marca 2004 [dostęp 2022-01-11].
Introduction, math.columbia.edu, 17 marca 2004 [dostęp 2022-01-11].
- ↑ Peter Woit, Not Even Wrong – The Failure of String Theory And the Search for Unity in Physical Law, Random House, 2006, ISBN 0-224-07605-1.
- ↑
 Luboš Motl, Book that is Not Even Wrong, blog The Reference Frame, 23 sierpnia 2005 [dostęp 2022-01-12].
Luboš Motl, Book that is Not Even Wrong, blog The Reference Frame, 23 sierpnia 2005 [dostęp 2022-01-12].
- ↑
 John Horgan, Why String Theory Is Still Not Even Wrong, Scientific American, scientificamerican.com, 27 kwietnia 2017 [dostęp 2022-01-11].
John Horgan, Why String Theory Is Still Not Even Wrong, Scientific American, scientificamerican.com, 27 kwietnia 2017 [dostęp 2022-01-11].
- ↑
 Peter Woit, Theories of Everything & Why String Theory is Not Even Wrong, kanał Lex Fridman na YouTube, 3 grudnia 2021 [dostęp 2022-01-13].
Peter Woit, Theories of Everything & Why String Theory is Not Even Wrong, kanał Lex Fridman na YouTube, 3 grudnia 2021 [dostęp 2022-01-13].
- ↑ Lee Smolin, The Trouble With Physics: The Rise of String Theory, the Fall of a Science, and What Comes Next, Boston: Houghton Mifflin, 2006, ISBN 978-0-618-55105-7, OCLC 64453453.
- ↑ Lee Smolin, Kłopoty z fizyką: Powstanie i rozkwit teorii strun, upadek nauki i co dalej, Jerzy Kowalski-Glikman (tłum.), Warszawa: Prószyński i S-ka, 2008, ISBN 978-83-7469-835-1, OCLC 297634861.
- ↑ John Horgan, Physicist George Ellis Knocks Physicists for Knocking Philosophy, Falsification, Free Will, Scientific American, scientificamerican.com, 22 lipca 2014 [dostęp 2022-01-11].
- ↑
 Sabine Hossenfelder, String theory pros and cons, kanał autorki na YouTube, 22 października 2018 [dostęp 2022-01-12].
Sabine Hossenfelder, String theory pros and cons, kanał autorki na YouTube, 22 października 2018 [dostęp 2022-01-12].
- ↑
 Sean M. Carroll, The String Theory Backlash, (ang.) Discover Magazine, discovermagazine.com, 19 czerwca 2006 [dostęp 2022-01-13].
Sean M. Carroll, The String Theory Backlash, (ang.) Discover Magazine, discovermagazine.com, 19 czerwca 2006 [dostęp 2022-01-13].
- ↑
 Sean M. Carroll, String theory: It's not dead yet, New Scientist, newscientist.com, 16 maja 2007 [dostęp 2022-01-13].
Sean M. Carroll, String theory: It's not dead yet, New Scientist, newscientist.com, 16 maja 2007 [dostęp 2022-01-13].
- ↑ String Theory, With No Holds Barred, science.org, 29 marca 2007 [dostęp 2022-01-13].
- ↑
 Big Bang Theory Quote 5393, the-big-bang-theory.com [dostęp 2022-01-14].
Big Bang Theory Quote 5393, the-big-bang-theory.com [dostęp 2022-01-14].
Literatura przedmiotu[edytuj | edytuj kod]
Popularnonaukowa[edytuj | edytuj kod]
- 2001: Greene, Brian, Piękno Wszechświata: Superstruny, ukryte wymiary i poszukiwanie teorii ostatecznej, Prószyński i S-ka, Warszawa, ISBN 83-7255-178-2.
- 2008: Kaku, Michio, Physics of the Impossible. A scientific exploration into the world of phasers, force fields, teleportation and time travel.
- 2009: Fizyka rzeczy niemożliwych. Fazery, pola siłowe, teleportacja i podróże w czasie, Prószyński i S-ka, ISBN 978-83-7648-145-6.
- 2011: II wydanie polskie, ISBN 978-83-7648145-6.
- 2011: Susskind, Leonard, Kosmiczny krajobraz. Dalej niż teoria strun, Prószyński i S-ka, Warszawa, ISBN 978-83-7648-852-3
Akademicka[edytuj | edytuj kod]
- 2005: Polchinski, Joseph, String Theory. A modern textbook, Cambridge University Press.
- Vol. 1: An introduction to the bosonic string, ISBN 978-0-511-33821-2
- Vol. 2: Superstring theory and beyond, ISBN 0-511-33821-X
Linki zewnętrzne[edytuj | edytuj kod]
 Teoria strun w Polsce, stringtheory.pl [dostęp 2022-01-12] – strona zawiera m.in. kalendarz polskich konferencji na ten temat, organizowanych od 2010 roku.
Teoria strun w Polsce, stringtheory.pl [dostęp 2022-01-12] – strona zawiera m.in. kalendarz polskich konferencji na ten temat, organizowanych od 2010 roku.
![]() Nagrania na YouTube (ang.) [dostęp 2023-05-21]:
Nagrania na YouTube (ang.) [dostęp 2023-05-21]:
- Brian Greene, Making sense of string theory, kanał TED, 23 kwietnia 2008;
- Edward Witten, Newton Lecture 2010: String theory and the Universe, części 1 i 2, kanał Institute of Physics, 10 sierpnia 2012.
- Don Lincoln, Superstrings, kanał Fermilabu, 12 stycznia 2015;
- Lee Smolin, String Theory Is Still Wrong, kanał Dr Brian Keating, 27 maja 2021.
- PWN: 3980562
- Britannica: science/string-theory
- Treccani: teoria-delle-stringhe, la-grande-scienza-teoria-delle-stringhe_(Storia-della-Scienza), la-grande-scienza-teoria-delle-stringhe-una-testimonianza_(Storia-della-Scienza)
- Universalis: theorie-des-cordes
- БРЭ: 4170089
- SNL: strengteori
- Catalana: 0144410


