Obliczenia równoległe

Obliczenia równoległe – forma wykonywania obliczeń, w której wiele instrukcji jest wykonywanych jednocześnie[1]. Taka forma przetwarzania danych była wykorzystywana przez wiele lat, głównie przy wykorzystaniu superkomputerów, a szczególne znaczenie zyskała z uwagi na fizyczne ograniczenia uniemożliwiające dalsze zwiększanie częstotliwości taktowania procesorów. Obliczenia równoległe stały się dominującym wzorcem w architekturze komputerowej, głównie za sprawą upowszechnienia procesorów wielordzeniowych[2].
Ze względu na skalę można wyróżnić obliczenia równoległe na poziomie:
- bitów,
- instrukcji,
- danych,
- zadań.
Ze względu na poziom, na którym sprzęt wspomaga operacje równoległe, można wyróżnić komputery:
- jednoprocesorowe wielordzeniowe (zawierające jeden procesor wielordzeniowy),
- symetryczne wieloprocesorowe (zawierające kilka identycznych, równorzędnych procesorów),
- systemy składające się z wielu maszyn:
Do prowadzenia obliczeń równoległych, oprócz sprzętu, konieczne są również odpowiednie algorytmy nazywane równoległymi. Są one trudniejsze w implementacji niż sekwencyjne[3], ponieważ współbieżność wprowadza dodatkowe możliwości popełnienia błędu. Powstają również dodatkowe problemy w uzyskaniu wysokiej wydajności z powodu dodatkowych nakładów na komunikację i konieczność synchronizacji obliczeń.
Obliczenia zależne, niezależne i granica ich przyspieszania[edytuj | edytuj kod]
W przetwarzaniu sekwencyjnym, aby rozwiązać problem obliczeniowy, tworzony jest algorytm, który składa się z ciągu instrukcji. Instrukcje te są wykonywane, w ustalonej kolejności na jednej jednostce obliczeniowej. Nie można wykonywać więcej niż jednej instrukcji jednocześnie – po ukończeniu jednej instrukcji, wykonywana jest kolejna[4].
W obliczeniach równoległych, aby rozwiązać dany problem, wykorzystuje się wiele jednostek obliczeniowych jednocześnie. Można tak postąpić, dzieląc problem na mniejsze, niezależne części, z których jedna może być wykonywana niezależnie od pozostałych. Jeśli uda się przeprowadzić taki podział, każda z części może być wykonana na innej jednostce obliczeniowej w tym samym czasie co pozostałe[4].
Wyodrębnienie tych niezależnych części jest kluczowe w implementacji algorytmów równoległych. Żaden program nie może być wykonany szybciej niż najdłuższy łańcuch zależnych od siebie obliczeń (znanych jako ścieżka krytyczna), ponieważ obliczenia, które są zależne od poprzednich obliczeń w łańcuchu, muszą być wykonywane po sobie. Jednak większość algorytmów nie składa się tylko z długich łańcuchów zależnych od siebie obliczeń; najczęściej pojawia się możliwość wykonania niezależnych obliczeń równolegle.
Warunki Bernsteina[edytuj | edytuj kod]
Niech Pi i Pj będą dwoma fragmentami programu. Warunki Bernsteina[5] opisują, kiedy dwa fragmenty są niezależne od siebie i mogą być wykonane równolegle bez żadnych przeszkód. Niech Ii będzie zbiorem wszystkich zmiennych wejściowych dla Pi, a Oi zbiorem jego zmiennych wyjściowych (podobnie Ij i Oj dla Pj). Pi i Pj są niezależne, jeśli spełniają następujące warunki:
Naruszenie pierwszego lub drugiego warunku wprowadza zależność przepływu, odpowiadającą sytuacji, w której wynikiem działania Pi jest wartość wykorzystywana przez Pj (lub odwrotnie). Trzeci warunek to wymaganie niezależności wyjścia. W sytuacji, gdy dwie wartości są zapisywane w jednym miejscu, to druga nadpisze pierwszą[6].
Przykład 1[edytuj | edytuj kod]
Poniżej przedstawiono dwie funkcje. Pierwsza zawiera przykładowe operacje zależne, a druga niezależne:
1: function Zależne(a, b) 2: c := a·b 3: d := 2·c 4: end function
Operacja 3 w Zależne(a, b) nie może być wykonana przed (czy nawet równolegle z) operacją 2, ponieważ operacja 3 wykorzystuje wynik z operacji 2. Narusza warunek 1 i w konsekwencji wymusza określony przepływ sterowania.
1: function Niezależne(a, b) 2: c := a·b 3: d := 2·b 4: e := a+b 5: end function
W tym przykładzie nie ma żadnych zależności pomiędzy operacjami, a więc mogą one być wykonane równolegle.
Przykład 2[edytuj | edytuj kod]
Spełnienie warunków Bernsteina może zależeć również od tego, w jaki sposób zapisano program. Przykładowo w funkcji
1: function ZależneII(a, b) 2: a := b + 5 3: c := a + 10 4: end function
wartość c zależy od wyliczanego wcześniej a. Można jednak w prosty sposób usunąć tę zależność i napisać równoważnie:
1: function NiezależneII(a, b) 2: a := b + 5 3: c := b + 15 4: end function
Warunki Bernsteina nie zezwalają na współdzielenie pamięci, a w konsekwencji na wymianę informacji pomiędzy podprogramami. Aby zapewnić możliwość komunikacji, potrzebne jest więc ustalanie kolejności między dostępami do pamięci, korzystając z takich technik jak semafory, bariery czy inne techniki synchronizacji.
Sytuacje wyścigu, wzajemne wykluczanie, synchronizacja i spowolnienie równoległe[edytuj | edytuj kod]
Podczas wykonywania programu równoległego, poszczególne jego podzadania[7] komunikują się ze sobą, a ich poszczególne instrukcje mogą się przeplatać w dowolny sposób. W poniższym przykładzie dwa podzadania operują na współdzielonej zmiennej
| Podzadanie A | Podzadanie B |
| 1A: Odczytaj zmienną V | 1B: Odczytaj zmienną V |
| 2A: Dodaj 1 do zmiennej V | 2B: Dodaj 1 do zmiennej V |
| 3A: Zapisz wartość w zmiennej V | 3B: Zapisz wartość w zmiennej V |
Jeśli instrukcja 1B zostanie wykonana pomiędzy 1A i 3A, lub jeśli instrukcja 1A zostanie wykonana pomiędzy 1B i 3B, to wynik działania programu będzie nieprawidłowy. Zjawisko to jest znane jako wyścigi lub hazard (ang. race conditions), a fragment programu, który nie powinien być wykonywany przez kilka podzadań jednocześnie, nazywamy sekcją krytyczną. W takim przypadku jak powyżej programista powinien zapewnić wzajemne wykluczanie pomiędzy podzadaniami w dostępie do zmiennej Można to osiągnąć, stosując blokady – konstrukcje programistyczne, dzięki którym tylko jedno podzadania ma dostęp do określonego zasobu. Powyższy fragment programu przepisany z użyciem blokad mógłby zostać przepisany w następujący sposób:
| Podzadanie A | Podzadanie B |
| 1A: Zablokuj zmienną V | 1B: Zablokuj zmienną V |
| 2A: Odczytaj zmienną V | 2B: Odczytaj zmienną V |
| 3A: Dodaj 1 do zmiennej V | 3B: Dodaj 1 do zmiennej V |
| 4A: Zapisz wartość w zmiennej V | 4B: Zapisz wartość w zmiennej V |
| 5A: Odblokuj zmienną V | 5B: Odblokuj zmienną V |
Tylko jedno z podzadań z sukcesem zablokuje zmienną i uzyska do niej wyłączny dostęp, podczas gdy drugie będzie musiało czekać na jej odblokowanie. Zastosowanie powyższej konstrukcji daje gwarancję poprawnego wykonania programu, kosztem jest jednak jego spowolnienie, które może być znaczne.
Blokowanie wielu zmiennych przy użyciu nieatomowych blokad może spowodować zakleszczenie. Atomowość blokady to własność, która gwarantuje, że wszystkie zmienne blokowane są razem, to znaczy, jeśli dwa podzadania próbują zablokować kilka zmiennych, to uda się to tylko jednemu z nich i blokada powstanie na wszystkich zmiennych. Jeśli natomiast blokady nie są atomowe, to może się zdarzyć, że jeśli dwa podzadania próbują zablokować te same dwie zmienne, to jeden z nich zablokuje jedną, a drugi drugą. W powstałej sytuacji oba podzadania czekają na siebie nawzajem i żaden z nich nie może zakończyć działania. Taką sytuację nazywamy zakleszczeniem.
Wiele programów równoległych wymaga by ich podzadania były dodatkowo synchronizowane. Taką możliwość daje użycie bariery. Bariery są zwykle implementowane za pomocą blokad. Wyróżnia się klasa algorytmów, w których nie używa się ani blokad ani barier (ang. lock-free and wait-free algorithms). Jednak stosowanie tego podejścia napotyka spore trudności (za przedstawienie eleganckich dowodów, wykorzystujących elementy topologii algebraicznej, niemożliwości rozwiązania dość prostych problemów przyznano Nagrodę Gödla w 2004 roku).
Nie każda próba „zrównoleglenia” daje efekt w postaci przyspieszenia obliczeń. W ogólności, jeśli program jest dzielony na coraz więcej i więcej podzadań, to w pewnym momencie narzuty związane z komunikacją zaczynają przeważać nad zyskiem ze „zrównoleglenia” i pomimo zwiększania teoretycznej mocy obliczeniowej mamy do czynienia ze spowolnieniem obliczeń. Zjawisko to nazywane jest spowolnieniem równoległym (ang. parallel slowdown). Próbą górnego oszacowania możliwego przyspieszenia uzyskanego przez zrównoleglenie obliczeń dają prawa: Amdahla i Gustafsona.
Prawa Amdahla i Gustafsona[edytuj | edytuj kod]
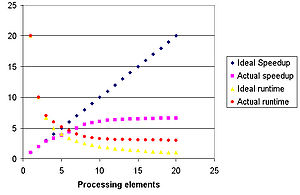
Teoretycznie, przyspieszenie spowodowane zrównolegleniem mogłoby być co najwyżej liniowe – podwojenie liczby jednostek obliczeniowych nie może zmniejszyć czasu obliczeń o więcej niż połowę, jednak w praktyce osiągnięcie optymalnego przyspieszenia nie jest możliwe. Większość realizacji osiąga przyspieszenie bliskie optymalnemu tylko dla małej liczby jednostek obliczeniowych.
Potencjalne przyspieszenie algorytmu na platformie korzystającej z obliczeń równoległych jest określone przez prawo Amdahla sformułowane w latach 60. XX wieku[8]. Prawo to wychodzi z założenia, że duży matematyczny czy inżynierski problem typowo składa się z takich części, które udaje się zrównoleglić i z takich, dla których nie jest to możliwe. Prawo Amdahla stanowi, iż fragmenty programu, które nie mogą być zrównoleglone, ograniczają możliwe do osiągnięcia przyspieszenie całego procesu. Ten związek jest definiowany przez następujące równanie:
gdzie: jest maksymalnym, możliwym do osiągnięcia przyspieszeniem programu (jako ułamek swojej pierwotnej prędkości w przypadku wykonywania sekwencyjnego), a jest ułamkiem, który określa jaką część obliczeń można „zrównoleglić”. Na przykład jeśli sekwencyjna część programu stanowi 10% całkowitego czasu potrzebnego na jego wykonanie to można osiągnąć nie więcej niż 10-krotne przyspieszenie, niezależnie od ilości procesorów jakie zostaną dodane. Tworzy to odgórny limit przydatności dodawania większej ilości jednostek obliczeniowych. „Jeśli zadanie nie może być podzielone z uwagi na ograniczenia wynikające z sekwencyjności problemu, dodanie mocy przetwarzania nie wpłynie na czas jego wykonania. Ciąża u ludzi trwa dziewięć miesięcy, obojętnie, ile kobiet uczestniczy w jej utrzymaniu”[9].

Kolejne prawo, nazywane Prawem Gustafsona (ang. Gustafson’s law) jest blisko spokrewnionym z prawem Amdahla. Gustafson w swojej pracy[10] argumentował, że co prawda dla ustalonego rozmiaru problemu, prawo Amdahla jest słuszne, jednak z jego praktyki badawczej wynika, że dysponując większą liczbą procesorów, próbuje się również rozwiązywać większe problemy, co z kolei powoduje, że coraz większa część obliczeń jest możliwa do zrównoleglenia.
Inne ograniczenie możliwości „zrównoleglania” algorytmów pochodzi z teorii złożoności obliczeniowej. Podobnie jak dla obliczeń sekwencyjnych istnieje klasa problemów NP-zupełnych, tak w obliczeniach równoległych istnieje klasa problemów P-zupełnych, których dobre „zrównoleglenie” jest prawdopodobnie niemożliwe[11].
Równoległość drobno- i gruboziarnista[edytuj | edytuj kod]
Aplikacje mogą być klasyfikowane pod względem tego, jak często podzadania wymagają synchronizacji lub komunikują się ze sobą. Mówimy o równoległości drobnoziarnistej (ang. fine-grained), jeśli komunikacja następuje wielokrotnie w ciągu sekundy, a gruboziarnistej (ang. coarse-grained), jeśli występuje rzadziej. Z najłatwiejszym przypadkiem mamy do czynienia, gdy komunikacja nie występuje w ogóle lub sporadycznie (żargonowo taką sytuację określa się jako embarrassing parallelism).
Modele spójności[edytuj | edytuj kod]

W systemach przetwarzania równoległego w celu przyspieszenia wykonywania operacji na pamięci współdzielonej stosuje się lokalne pamięci podręczne i buforowanie operacji zapisu[12]. Istnienie tych mechanizmów może prowadzić do niespójności (dla różnych procesów te same, wspólne dane mogą przez pewien czas mieć różne wartości). Jako przykład można podać następującą sekwencję instrukcji (x i y są zmiennymi współdzielonymi, początkowo obie są równe 0):
| Wątek A | Wątek B |
| 1A: Podstaw wartość x do ax | 1B: dodaj 1 do y |
| 2A: Podstaw wartość y do ay | 2B: dodaj 1 do x |
| 3A: Sprawdź, czy ax jest większe lub równe ay | 3B: nic nie rób |
Realizacja wspomnianych mechanizmów może dopuścić sytuację, gdy aktualizacja zmiennych x i y jest dostarczana do wątku A w zmienionej kolejności, a więc mogłoby się zdarzyć, że wynik porównania w 3A byłby fałszywy. W związku z tym języki programowania równoległego i komputery równoległe muszą posiadać model spójności (ang. consistency model), który definiuje zasady wykonywania operacji na zmiennych współdzielonych w pamięci komputera oraz w jaki sposób powstają wyniki tych operacji.
Jednym z pierwszych modeli spójności był model spójności sekwencyjnej Lesliego Lamporta. Spójność sekwencyjna oznacza, że wyniki każdego możliwego działania programu równoległego są takie same jak wynik działania dla pewnego ustalonego sekwencyjnego wykonania tych operacji, przy czym kolejność wykonywania operacji przez każdy pojedynczy procesor zgadza się z kolejnością wykonania zapisaną w jego programie[13].
Powszechnym modelem spójności pamięci jest STM (ang. software transactional memory, w którym używa się koncepcji atomowych transakcji zapożyczonej z teorii baz danych.
Modele spójności pamięci mogą być przedstawiane formalnie na wiele sposobów. Wczesnym matematycznym modelem dla dyskretnych systemów rozproszonych są sieci Petriego, które Carl Adam Petri zdefiniował w swojej rozprawie doktorskiej w 1962 roku.
Taksonomia Flynna i typy zrównoleglania[edytuj | edytuj kod]
Taksonomia Flynna[edytuj | edytuj kod]
Michael J. Flynn stworzył jedną z najwcześniejszych klasyfikacji systemów dla równoległych (i sekwencyjnych) komputerów i programów, znaną jako taksonomia Flynna. Flynn zaklasyfikował programy i komputery według tego, czy dany program lub komputer korzysta z jednego, czy z wielu zbiorów instrukcji oraz czy te instrukcje korzystają z jednego, czy z wielu zbiorów danych.
W obrębie podziału Flynn wyróżnił cztery klasy: SISD (ang. single-instruction-single-data) równoważną przetwarzaniu całkowicie sekwencyjnemu; SIMD (ang. single-instruction-multiple-data), gdzie wykonuje się te same operacje na różnych zbiorach danych – jak to ma często miejsce przy przetwarzaniu sygnałów; MISD (ang. multiple-instruction-single-data) to rzadko używana klasa, w której wykonujemy różne operacje na tym samym zbiorze danych (zob. systolic arrays); i w końcu MIMD (ang. Multiple-instruction-multiple-data), gdzie różne operacje wykonywane są na różnych zbiorach danych – jest to najczęstszy przypadek w przetwarzaniu równoległym.
Według Davida Pattersona i Johna Hennesy’a, „Niektóre maszyny są oczywiście hybrydami tych kategorii, jednak ten klasyczny model przetrwał, ponieważ jest prosty, łatwy do zrozumienia i daje dobry pierwszy ogląd zagadnienia. Jest również – prawdopodobnie dzięki swojej zrozumiałości – najbardziej powszechnym schematem”[14].
Inny podział można przeprowadzić nie ze względu na typ systemu, ale skalę, w jakiej odbywa się zrównoleglanie. Wyróżniamy wtedy obliczenia równoległe: na poziomie bitów, instrukcji, danych oraz zadań.
Zrównoleglanie na poziomie bitów[edytuj | edytuj kod]
Poczynając od powszechnego zastosowania technologii VLSI (produkcji układów scalonych o wielkiej skali integracji) w latach 70. aż do roku około 1986 przyspieszenie działania komputerów było uzyskiwane poprzez podwajanie długości słowa maszynowego (czyli podstawowej jednostki informacji przetwarzanej przez procesor w jednym cyklu, w uproszczeniu jest to liczba bitów będąca rozmiarem szyny danych oraz rejestrów procesora)[15]. Zwiększenie rozmiaru słowa maszynowego zmniejsza liczbę instrukcji, jaką procesor musi wykonać, realizując operację na zmiennych, których rozmiar jest większy niż długość słowa maszynowego. Na przykład jeśli 8-bitowy procesor realizuje dodawanie dwóch 16-bitowych liczb całkowitych, to trzeba oddzielnie wykonać działanie na młodszych i, z uwzględnieniem przeniesienia (ang. carry bit), starszych bajtach obu liczb. Tak więc w tym przypadku konieczne było wykonanie dwóch dodawań 8-bitowych, podczas gdy 16-bitowy procesor mógłby wykonać tę operację jako jedną instrukcję.
Historycznie, 4-bitowe procesory zostały zastąpione 8-bitowymi, te z kolei 16-bitowymi, a następnie 32-bitowymi. Ten trend nieco się zatrzymał, gdyż procesory 32-bitowe stały się standardem aż do lat 2003–2004, gdy na rynku upowszechniły się procesory z architekturą 64-bitową.
Zrównoleglanie na poziomie instrukcji[edytuj | edytuj kod]

Program komputerowy, technicznie rzecz biorąc, jest ciągiem instrukcji wykonywanym przez procesor. Instrukcje te mogą być grupowane, a kolejność ich wykonania zmieniana w taki sposób, aby można było wykonać je równolegle bez zmiany wyniku programu. Technika ta nazywana jest zrównoleglaniem na poziomie instrukcji, postęp w jej stosowaniu zdominował rozwój architektury komputerów od połowy lat 80. do połowy lat 90. XX wieku[16].
Współczesne procesory posiadają wielostopniowe potoki instrukcji. Każdy stopień potoku odpowiada za inną czynność, jaką procesor wykonuje na danej instrukcji w danym etapie; innymi słowy, proces z -stopniowym potokiem może posiadać do różnych instrukcji na różnym etapie wykonywania. Klasycznym przykładem potokowego procesora jest procesor RISC z pięciostopniowym potokiem: pobranie instrukcji, zdekodowanie instrukcji, wykonanie instrukcji, dostęp do pamięci oraz zapisanie wyników działania instrukcji do rejestru. Procesor Pentium 4 ma 35-stopniowy potok[17].

Niektóre procesory mogą wykonywać więcej niż jedną instrukcję w ciągu cyklu, stosując inne techniki niż przetwarzanie potokowe opisane powyżej. Procesory te, nazywane superskalarnymi, grupują, przestawiają instrukcje niepowiązane zależnością danych i wykonują je jednocześnie. Dwie najczęściej stosowane w tym celu techniki to technika notowania (ang. scoreboarding) i podobna, nazywana algorytmem Tomasulo, w której stosuje się przemianowanie rejestrów (ang. register renaming).
Możliwe jest również wykonywanie instrukcji, co do których nie ma jeszcze pewności, czy powinny być wykonane, aby ostatecznie przyjąć lub odrzucić wyniki ich działania. Jest to tak zwane spekulatywne wykonywanie instrukcji.
Zrównoleglanie przetwarzania danych[edytuj | edytuj kod]
Zrównoleglanie przetwarzania danych jest właściwe przetwarzaniu iteracyjnemu i skupia się na rozdzielaniu danych pomiędzy różne jednostki obliczeniowe w taki sposób, aby zminimalizować ich wzajemne zależności. Na poziomie kodu źródłowego mówi się o zrównoleglaniu pętli (ang. parallelization of loops), gdzie często wykonuje się podobne (niekoniecznie identyczne) ciągi operacji na elementach dużej struktury”[18]. Tego typu równoległość wykorzystuje wiele naukowych i inżynierskich aplikacji.
Rozdzielenie danych nie zawsze jest możliwe. Jeśli na przykład obliczenia w każdej kolejnej iteracji zależą od wyników poprzedniej, to zrównoleglenie pętli nie jest możliwe. Taka zależność ma miejsce w poniższym przykładzie obliczającym pierwsze kilka liczb z ciągu Fibonacciego:
1: prev2 := 0 2: prev1 := 1 3: cur := 1 4: do: 5: CUR := PREV1 + PREV2 6: PREV2 := PREV1 7: PREV1 := CUR 8: while (CUR < 10)
Pętla ta nie może zostać zrównoleglona, ponieważ zmienne (PREV1) i PREV2 użyte do obliczenia CUR są na nowo obliczane w każdym obiegu pętli.
Zrównoleglanie zadań[edytuj | edytuj kod]
Zrównoleglanie zadań jest cechą charakterystyczną programu, w którym „zupełnie różniące się obliczenia mogą być wykonywane na tych samych lub innych zbiorach danych”[18]. Różni się ono od zrównoleglania danych, gdzie te same obliczenia wykonywane są na tych samych lub innych zbiorach danych. Programy charakteryzujące się zrównolegleniem zadań zwykle nie skalują się dobrze wraz ze wzrostem rozmiaru problemu[19].
Sprzęt[edytuj | edytuj kod]
Pamięć i komunikacja[edytuj | edytuj kod]
Pamięć operacyjna w komputerze równoległym jest pamięcią współdzieloną przez wszystkie jednostki w jednej przestrzeni adresowej, lub pamięcią rozproszoną, w której każda jednostka prowadzi obliczenia we własnej przestrzenie adresowej[20]. Pojęcie pamięci rozproszonej oznacza logiczny podział przestrzeni adresowych (fizycznie mogą one należeć do tej samej maszyny), choć zwykle oznacza to również rozproszenie fizyczne. Rozproszona pamięć dzielona odnosi się do połączenia powyższych koncepcji, gdzie logicznie pamięć jest współdzielona, chociaż fizycznie mamy do czynienia z pamięcią rozproszoną (każda jednostka ma swoją fizyczną pamięć lokalną, ale na poziomie logicznym/programowym ma dostęp do pamięci innych jednostek). Rozproszona pamięć dzielona jest więc symulacją pamięci współdzielonej, co ułatwia tworzenie oprogramowania, a jednocześnie może powodować opóźnienia (dostęp do pamięci lokalnej jest typowo znacznie szybszy niż dostęp do pamięci zdalnej).
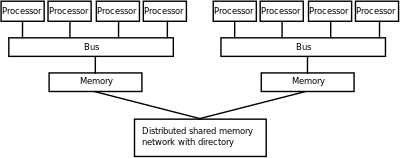
Architektury komputerowe, w których cała pamięć operacyjna jest dostępna z takim samym opóźnieniem i częstotliwością, są nazywane UMA (ang. Uniform Memory Access). Tę cechę mogą mieć właściwie tylko systemy z pamięcią dzieloną. Pozostałe systemy określamy mianem NUMA (ang. Non-Uniform Memory Access) – do tej kategorii zaliczamy systemy z pamięcią rozproszoną.
W celu poprawy wydajności systemu komputerowego stosuje się niewielkie, ale szybkie pamięci podręczne (ang. cache memory), które mogą przechowywać tymczasowe dane. Stosowanie ich w architekturach równoległych nastręcza problemy związane z zachowaniem spójności danych (ang. cache coherency), gdyż te same dane mogą być przechowywane w pamięciach podręcznych różnych procesorów. Zapewnienie poprawności obliczeń wymusza stosowanie dodatkowych technik, z których najpopularniejsza to bus snooping. Mimo ich istnienia projektowanie wydajnych pamięci podręcznych przysparza wiele trudności, dlatego architektury oparte na pamięci dzielonej należą do trudniej skalowalnych niż te oparte na pamięci rozproszonej[20].
Komunikacja pomiędzy dwoma procesorami oraz procesorem i pamięcią może zostać zrealizowana sprzętowo na kilka sposobów: poprzez wieloportową (ang. multiported) lub multipleksowaną pamięć dzieloną, przełącznicę krzyżową (ang. crossbar switch), współdzieloną magistralę (ang. shared bus) lub sieć o jednej z wielu topologii (gwiazdy, pierścienia, drzewa, hiperkostki i innych). Komputery równoległe zbudowane w oparciu o sieć (ang. interconnect network) wymagają jakiejś formy wyboru tras połączeń (ang. routing) dla procesorów, które nie są bezpośrednio połączone. Medium użyte do komunikacji pomiędzy procesorami zwykle ma strukturę hierarchiczną, zwłaszcza w przypadku dużej liczby procesorów.
Typy komputerów równoległych[edytuj | edytuj kod]
Komputery równoległe można podzielić ze względu na poziom, na jakim sprzęt zrównolegla operacje. Klasyfikacja w dużym stopniu odpowiada temu, jak bardzo są fizycznie oddalone od siebie poszczególne jednostki obliczeniowe. Przynależność do jednej z grup nie wyklucza jednak przynależności do pozostałych. Do często spotykanych kombinacji należą na przykład klastry wieloprocesorów symetrycznych.
Procesory wielordzeniowe[edytuj | edytuj kod]
Procesor wielordzeniowy to procesor z kilkoma jednostkami wykonawczymi („rdzeniami”). Procesory te różnią się od procesorów superskalarnych, gdyż mogą wykonywać jednocześnie instrukcje pochodzące z różnych ciągów instrukcji; w przeciwieństwie do tych drugich, które co prawda również mogą w pewnych warunkach wykonywać kilka instrukcji jednocześnie, ale pochodzących z jednego ciągu instrukcji (w danej chwili wykonują tylko jeden wątek). Potencjalnie każdy z rdzeni może być jednostką superskalarną.
Wczesną formą procesorów wielordzeniowych była technologia SMT, inaczej wielowątkowość współbieżna (ang. simultaneous multithreading), którą zastosowano na przykład w procesorach i Pentium 4 (zob. Hyper-Threading). Procesor z technologią SMT ma tylko jeden rdzeń, ale kiedy jest bezczynny (ang. idle), na przykład z powodu konieczności odwołania poza pamięć podręczną (ang. cache miss), może go wykorzystać do wykonywania kolejnego wątku. Jako faktycznie wielordzeniowe procesory można wymienić architektury Core oraz Cell.
Symetryczne systemy wieloprocesorowe[edytuj | edytuj kod]
Wieloprocesor symetryczny (SMP – ang. symmetric multiprocessor) to system komputerowy z wieloma identycznymi procesorami, które operują na wspólnej pamięci za pośrednictwem magistrali (ang. bus)[21]. Z powodu zastosowania magistrali rozwiązanie to jest jednak słabo skalowalne, dlatego zwykle maszyny SMP posiadają nie więcej niż 32 procesory[22]. Stosowanie dużych pamięci podręcznych, co ogranicza wykorzystanie magistrali, i niewielkich rozmiarów procesorów powoduje, że przy założeniu dostatecznie szybkiego dostępu do pamięci, symetryczne systemy wieloprocesorowe są bardzo wydajne przy stosunkowo niewielkich kosztach[21].
Przetwarzanie rozproszone[edytuj | edytuj kod]
Przetwarzanie rozproszone (znane też jako wieloprocesor o rozproszonej pamięci) jest systemem komputerowym o rozproszonej pamięci, w którym elementy przetwarzające połączone są przez sieć komputerową. Komputery rozproszone są wysoce skalowalne[23].
Przetwarzanie klastrowe[edytuj | edytuj kod]

Klaster jest grupą komputerów, które w pewnych aspektach mogą być traktowane jako pojedynczy komputer[24]. Klastry składają się z wielu niezależnych komputerów połączonych siecią. Podczas gdy maszyny w klastrze nie muszą być symetryczne, równoważenie obciążenia jest trudniejsze, jeśli nie są. Jednym z typów klastra jest Beowulf, który jest zaimplementowany na wielu identycznych komputerach połączonych siecią lokalną Ethernet opartą na protokole TCP/IP[25]. Technologia Beowulf została stworzona przez Thomasa Sterlinga i Donalda Beckera. Znaczna część superkomputerów z listy TOP500 to klastry[26].
Komputery masowo równoległe[edytuj | edytuj kod]
Masowo równoległy komputer (ang. Massively Parallel Processor) jest jednym komputerem z wieloma połączonymi ze sobą procesorami. Komputer ten posiada wiele podobnych cech do klastrów, jednak jest on zazwyczaj większy i posiada o wiele więcej niż 100 procesorów.[27] W komputerze masowo równoległym „każdy procesor posiada swoją własna pamięć oraz kopię systemu operacyjnego i aplikacji. Każdy podsystem komunikuje się z innymi poprzez szybkie łącza”[28].

Blue Gene/L, najszybszy według rankingu TOP500 w 2007 roku, superkomputer na świecie jest komputerem masowo równoległym.
Obliczenia w gridach[edytuj | edytuj kod]
Obliczenia w gridach to najbardziej rozproszona forma obliczeń równoległych. Mamy tu do czynienia z komputerami połączonymi siecią Internet, których zasoby używane są do rozwiązania danego problemu. Ze względu na niewielką przepustowość i duże opóźnienia łączy, zwykle tylko problemy, które wymagają niewiele komunikacji, są rozwiązywane w ten sposób. Wśród realizacji obliczeń gridowych można wymienić SETI@home i Folding@home jako szerzej znane.
Większość aplikacji korzysta z warstwy pośredniej (ang. middleware) – oprogramowania, które, działając na poziomie pomiędzy system operacyjnym a aplikacjami, dostarcza usług związanych z wykorzystaniem zasobów sieciowych. Jako przykład można wymienić system BOINC (ang. Berkeley Open Infrastructure for Network Computing), który pierwotnie powstał dla potrzeb projektu SETI@home.
Specjalistyczne urządzenia do przetwarzania równoległego[edytuj | edytuj kod]
Obliczenia równoległe można wykonywać nie tylko w komputerach ogólnego przeznaczenia, ale i w specjalnie zaprojektowanych urządzeniach. Rozwiązanie to zwykle opłaca się stosować do rozwiązywania dość ograniczonej klasy zagadnień równoległych.
- Rekonfigurowalne Systemy Obliczeniowe
System rekonfigurowalny składa się z procesora ogólnego przeznaczenia oraz programowalnych układów logicznych FPGA (ang. field-programmable gate array).
Układy FPGA programuje się przy użyciu języków HDL (ang. Hardware Description Language) takich jak VHDL czy Verilog. Programowanie w tych językach może być jednak monotonne i męczące, dlatego powstało kilka narzędzi, które próbują emulować elementy składni i semantyki języka C, znanego większości programistów, tłumacząc je na język typu HDL. Jako przykłady takich rozwiązań można podać: Mitrion-C, Impulse C, DIME-C oraz Handel-C.
Upublicznienie specyfikacji technologii HyperTransport przez AMD umożliwiło dostęp do wysoko wydajnych, rekonfigurowalnych obliczeń stronom trzecim[29].
- GPGPU

Wykonywanie obliczeń ogólnego przeznaczenia za pomocą procesora karty graficznej (GPGPU, ang. General-Purpose Computing on Graphics Processing Units) to nowy kierunek badań w inżynierii komputerowej. Procesor karty graficznej (tzw. GPU) to koprocesor zoptymalizowany do obliczeń w grafice komputerowej[30], z których większość to podlegające łatwemu urównolegleniu algebraiczne operacje macierzowe wykonywane w arytmetyce zmiennopozycyjnej. Dlatego współczesne GPU posiadają architekturę masowo równoległą z setkami rdzeni obliczeniowych, a ich teoretyczna moc obliczeniowa sięga 1 TFLOPS (bilion operacji zmiennoprzecinkowych na sekundę).
Początkowo w programach wykorzystujących technikę GPGPU używano standardowych interfejsów programowania aplikacji graficznych, głównie DirectX i OpenGL, co było niewygodne i nieefektywne. Dlatego producenci kart graficznych udostępnili specjalne języki programowania i środowiska programistyczne dostosowane do tworzenia aplikacji w technologii GPGPU: CUDA dla procesorów firmy Nvidia oraz CTM i ATI Stream dla procesorów firmy AMD. Innymi środowiskami przeznaczonymi do pracy w technologii GPGPU są m.in. BrookGPU, PeakStream oraz RapidMind. Istnieje również niezależne od platformy sprzętowej i wspierane przez wszystkich liczących się producentów sprzętu środowisko OpenCL. Zarówno Nvidia, jak i AMD produkują tzw. procesory obliczeniowe, czyli specjalne karty graficzne dla technologii GPGPU: Tesla i FireStream.
- Specjalizowane układy scalone
Specjalizowane układy scalone (ASIC ang. application-specific integrated circuit) to układy projektowane do realizacji ściśle określonego zadania[31][32][33].
Zaletą układów ASIC, ze względu na specjalizację do określonego zadania, jest większa wydajność w porównaniu z komputerem ogólnego przeznaczenia. Jednak ze względu na wysoki koszt (stworzenie maski litograficznej może kosztować ponad milion dolarów[34], a im mniejsze tranzystory, tym droższa maska) może się okazać, że osiągnięty zysk jest iluzoryczny. W czasie potrzebnym na przygotowanie ASIC układy ogólnego przeznaczenia, których wydajność rośnie zgodnie z prawem Moore’a, mogły osiągnąć porównywalną wydajność[29]. Czynniki te powodują, że układy ASIC nie nadają się w większości zastosowań obliczeń równoległych. Jednym z nielicznych przykładów może być maszyna Riken MDGRAPE-3, gdzie użyto ASIC do symulacji dynamiki molekularnej.
- Procesory wektorowe

Procesor wektorowy jest procesorem lub systemem komputerowym, który wykonuje te same instrukcje na dużych zbiorach danych. „Procesory wektorowe posiadają operacje wysokiego poziomu, które działają na liniowych tablicach składających się z liczb lub wektorów. Przykładem operacji wektorowej jest gdzie i są 64-elementowymi wektorami złożonymi z 64-bitowych liczb zmiennoprzecinkowych”[35]. Procesory wektorowe są przykładem architektury klasy SIMD taksonomii Flynna[35].
Komputery Cray z procesorami wektorowymi stały się znane w latach 70. i 80. Ogólnie jednak procesory wektorowe przestały być popularne, zarówno jako CPU, jak i pełne systemy komputerowe, a nowoczesne maszyny używają tego typu przetwarzania danych poprzez dodatkowe zestawy rozkazów takie jak AltiVec, SSE i 3DNow!.
Oprogramowanie[edytuj | edytuj kod]
W celu ułatwienia programowania komputerów równoległych stworzono specjalne: języki programowania, interfejsy i biblioteki. Można je podzielić ze względu na architekturę pamięci, jaką zakładają: pamięć współdzieloną, pamięć rozproszoną, czy też rozproszoną pamięć dzieloną. Języki programowania oparte na pamięci dzielonej pozwalają operować na współdzielonych zmiennych, a te oparte na pamięci rozproszonej korzystają z przesyłania komunikatów (ang. message passing). POSIX Threads i OpenMP to dwa najczęściej używane interfejsy oparte na pamięci dzielonej, natomiast Message Passing Interface (MPI) to najczęściej używany interfejs korzystający z przesyłania komunikatów.
Zrównoleglanie automatyczne[edytuj | edytuj kod]
Automatyczne zrównoleglanie sekwencyjnego programu przez kompilator jest „świętym graalem” obliczeń równoległych. Mimo wieloletnich wysiłków osób pracujących nad rozwojem kompilatorów, osiągnięto jedynie częściowy sukces[36].
Popularne języki programowania równoległego pozostają albo jawnie równolegle (ang. explicitily parallel), albo (w najlepszym przypadku) częściowo niejawne (ang. partially implicit), kiedy to programista podaje kompilatorowi specjalne dyrektywy sterujące zrównoleglaniem. Istnieje kilka języków, w których zrównoleglanie odbywa się w pełni niejawnie: SISAL, Równoległy Haskell i (dla FPGA) Mitrion-C – są to jednak języki niszowe, które nie są powszechnie używane.
Mechanizm punktów kontrolnych[edytuj | edytuj kod]
Wraz ze wzrostem stopnia skomplikowania komputerów rośnie również liczba występujących błędów i zmniejsza się średni bezawaryjny czas ich pracy. Jedną z technik zapewniania poprawności obliczeń jest zapamiętywanie, w czasie działania aplikacji, tak zwanych punktów kontrolnych (ang. application checkpointing). Innymi słowy, system co jakiś czas zapamiętuje stan działania aplikacji wraz ze wszystkimi wykorzystywanymi zasobami (ang. core dump), aby w razie wystąpienia błędu wznowić obliczenia od ostatniego punktu kontrolnego, zamiast wykonywać je wszystkie od początku. Technika ta może również ułatwić migrację procesów.
Zastosowania[edytuj | edytuj kod]
Wraz z postępem w szybkości działania komputerów równoległych coraz więcej problemów, których rozwiązanie wcześniej nie było możliwe, jest w zasięgu dostępnych mocy obliczeniowych. Zastosowanie obliczeń równoległych obejmuje szerokie spektrum dziedzin nauki od bioinformatyki (zob. zwijanie białka) do ekonomii (symulacje w matematyce finansowej).
Typowe problemy, gdzie może być wykorzystane przetwarzanie równoległe, obejmują[37]:
- gęstą algebrę liniowa – metody numeryczne w algebrze liniowej, gdzie dane są macierzami lub wektorami gęstymi,
- rzadką algebrę liniową – metody numeryczne w algebrze liniowej, gdzie dane są macierzami lub wektorami rzadkimi,
- metody spektralne – dane są w dziedzinie częstotliwości (ang. Frequency domain) w odróżnieniu od dziedziny czasu i przestrzeni,
- symulacje zachowania układu ciał pod wpływem oddziaływań fizycznych (ang. N-body simulation), na przykład symulacja Barnesa-Huta (ang. Barnes-Hut simulation),
- obliczenia z rozmieszczeniem węzłów w siatce prostokątnej (ang. regular grid problems) takich jak metoda kratowa Boltzmanna (ang. Lattice Boltzmann methods) stosowana w mechanice płynów,
- obliczenia z nieregularnym rozmieszczeniem węzłów (ang. unstructured grid problems) tak jak w analizie metodą elementów skończonych,
- symulacje metodą Monte Carlo,
- zagadnienia związane z układami kombinacyjnymi takie jak atak typu brute force,
- problemy, w których występuje przeszukiwanie grafu,
- programowanie dynamiczne,
- algorytmy typu branch and bound,
- obliczenia w modelach grafowych (ang. graphical models) takie jak wykrywanie ukrytych modeli Markowa lub konstruowanie sieci bayesowskich),
- symulacja działania automatu skończonego.
Prowadzenie obliczeń równoległych na dużą skalę jest niezwykle kosztowne. Z tego powodu jednostki posiadające superkomputery (komputery równoległe o dużej mocy obliczeniowej) określa się mianem centrów obliczeniowych. W Polsce są to między innymi: ICM w Warszawie, TASK w Gdańsku, PCSS w Poznaniu i Cyfronet w Krakowie, a na świecie: Los Alamos National Laboratory i Lawrence Livermore National Laboratory w USA, EPCC w Wielkiej Brytanii i wiele innych.
Historia[edytuj | edytuj kod]

Początki obliczeń równoległych łączy się z pracą Luigi Federico Menabrei pod tytułem „Sketch of the Analytic Engine Invented by Charles Babbage” z 1842 roku[38][39]. Ponad sto lat później, w 1954 roku, IBM wprowadził na rynek komputer 704, według projektu, którego Gene Amdahl był jednym z głównych konstruktorów. Komputer ten stał się pierwszym urządzeniem dostępnym na rynku, które w pełni automatycznie używało rozkazów arytmetyki liczb zmiennoprzecinkowych[40]. W 1958, naukowcy z IBM John Cocke i Daniel Slotnick po raz pierwszy rozważali wykorzystanie przetwarzania równoległego w obliczeniach numerycznych[41]. Firma Burroughs w 1962 roku wprowadziła D825 – czteroprocesorowy komputer, który adresował 16 modułów pamięci przy użyciu przełącznicy krzyżowej[42]. W 1967 Gene Amdahl opublikował artykuł, w którym sformułowane zostało prawo nazwane później prawem Amdahla[43].
W 1969 Amerykański Honeywell wprowadził na rynek system Multics, który mógł zawierać do ośmiu procesorów[41]. Z kolei C.mmp był w latach 70. systemem składającym się z szesnastu minikomputerów PDP-11 (działał w Carnegie Mellon University)[39].
Początki komputerów typu SIMD sięgają lat 70. XX wieku, a motywacją ich konstruktorów była próba zamortyzowania czasu propagacji jednostki sterującej procesora przy przetwarzaniu kolejnych instrukcji[44]. W 1964 Slotnick zaproponował zbudowanie wieloprocesorowego komputera równoległego dla Laboratoriów Lawrence’a w Livermore (Kalifornia)[41]. Komputer ten (ILLIAC IV) został ufundowany przez Siły Powietrzne Stanów Zjednoczonych, co było pierwszą próbą konstrukcji komputera typu SIMD[41]. Projekt pozwalał na wyposażenie tego komputera nawet w 256 procesorów, co umożliwiało jednoczesne przetwarzanie wielu zbiorów danych. Po jedenastu latach przedsięwzięcie, zrealizowane ostatecznie na Uniwersytecie Illinois, pochłonęło czterokrotnie więcej funduszy, niż pierwotnie zakładano[45] i kiedy w 1976 roku w końcu można było go użyć, ówczesne komputery, takie jak Cray-1, były już od niego bardziej wydajne.
Koniec ery skalowania częstotliwości[edytuj | edytuj kod]
Od połowy lat 80. do 2004 roku dominującym czynnikiem przyspieszającym działanie komputerów było zwiększanie częstotliwości zegara. Czas wykonywania programu jest równy liczbie instrukcji pomnożonej przez średni czas wykonywania instrukcji. Jeśli pozostałe parametry się nie zmieniają, to zwiększanie częstotliwości zegara zmniejsza średni czas, jaki potrzebny jest na wykonanie instrukcji. Wzrost częstotliwości zmniejsza zatem czas wykonywania wszystkich programów, w których prędkość procesora ma dominujący wpływ na szybkość ich wykonania (ang. computation-bounded programs)[46].
Pobór mocy danego układu scalonego określa wzór gdzie oznacza moc, – pojemność elektryczną związaną z kondensatorami ładowanymi i rozładowanymi przy każdym cyklu zegara (proporcjonalna do liczby tranzystorów, których sygnały wejściowe ulegają zmianie), napięciem, a częstotliwością procesora (liczba cykli zegara na sekundę)[47]. Wzrost częstotliwości zwiększa energię elektryczną pobieraną przez procesor i zamienianą na ciepło. Powiększający się pobór energii procesorów i związane z tym problemy z odprowadzaniem ciepła skłoniły firmę Intel w maju 2004 do zamknięcia projektu tworzenia procesorów Tejas i Jayhawk. Decyzja ta jest nazywana końcem dominującej roli zwiększania częstotliwości w ulepszaniu architektury komputerów[48].
Prawo Moore’a jest empiryczną obserwacją mówiącą, iż liczba tranzystorów w układzie scalonym podwaja się co 18–24 miesiące. Mimo problemów z poborem energii i częstych zapowiedzi jego końca, prawo Moore’a jest nadal aktualne. Wzrastające możliwości umieszczania w jednym układzie scalonym coraz większej liczby tranzystorów zmuszają do szukania kolejnych technik wykorzystania ich do zwiększenia szybkości obliczeń, np. budując koprocesory zrównoleglające obliczenia.
Zobacz też[edytuj | edytuj kod]
Przypisy[edytuj | edytuj kod]
- ↑ G.S. Almasi, A. Gottlieb, Highly Parallel Computing. Benjamin-Cummings publishers, Redwood city, CA, 1989.
- ↑ Krste Asanovic i in., The Landscape of Parallel Computing Research: A View from Berkeley (PDF). University of California, Berkeley. Raport Techniczny numer UCB/EECS-2006-183. 18 grudnia 2006: „Old [conventional wisdom]: Increasing clock frequency is the primary method of improving processor performance. New [conventional wisdom]: Increasing parallelism is the primary method of improving processor performance... Even representatives from Intel, a company generally associated with the 'higher clock-speed is better’ position, warned that traditional approaches to maximizing performance through maximizing clock speed have been pushed to their limit.”.
- ↑ David A. Patterson, John L. Hennessy, Computer Organization and Design (Second Edition), Morgan Kaufmann Publishers, 1998. ISBN 1-55860-428-6, s. 715.
- ↑ a b Blaise Barney: Introduction to Parallel Computing. [dostęp 2007-11-09]. [zarchiwizowane z tego adresu (2013-06-29)].
- ↑ A.J. Bernstein, Program Analysis for Parallel Processing, IEEE Trans. on Electronic Computers, EC-15, październik 1966, s. 757–762.
- ↑ Roosta, Seyed H., Parallel processing and parallel algorithms: theory and computation, 2000, Springer, ISBN 0-387-98716-9, s. 114.
- ↑ Podzadania składowe programu realizowanego równolegle mogą być wątkami tego samego procesu. Niektóre równolegle pracujące komputery zaprojektowane są tak, by wykorzystywać lżejsze odmiany wątków – włókna, możliwe jest również wykorzystanie oddzielnych procesów.
- ↑ G. Amdahl, The validity of the single processor approach to achieving large-scale computing capabilities, Materiały konferencyjne AFIPS Spring Joint Computer Conference, s. 483–485, Atlantic City, N.J., kwiecień 1967. AFIPS Press.
- ↑ Frederick P. Brooks Jr., The Mythical Man-Month: Essays on Software Engineering, rozdział 2 – The Mythical Man Month. ISBN 0-201-83595-9.
- ↑ Reevaluating Amdahl’s Law. scl.ameslab.gov. [zarchiwizowane z tego adresu (2012-06-23)]. Communications of the ACM 31(5), 1988. s. 532–533.
- ↑ Raymond Greenlaw, H. James Hoover, Walter L. Ruzzo: Limits to Parallel Computation: P-Completeness Theory. Oxford University Press, 1988.
- ↑ Janina Mincer-Daszkiewicz: Pamięć w systemach rozproszonych. [dostęp 2008-08-15].
- ↑ Leslie Lamport, How to Make a Multiprocessor Computer That Correctly Executes Multiprocess Programs, „IEEE Transactions on Computers”, C-28,9 (wrzesień 1979), s. 690–691.
- ↑ Patterson i Hennessy, s. 748.
- ↑ David E Culler, Parallel Computer Architecture – A Hardware/Software Approach, Jaswinder Pal Singh, Anoop Gupta, San Francisco: Morgan Kaufmann Publishers, 1999, s. 15, ISBN 1-55860-343-3, OCLC 39354251.
- ↑ Culler i inni, s. 15.
- ↑ Yale Patt, The Microprocessor Ten Years From Now: What Are The Challenges, How Do We Meet Them? (wmv). Wykład wygłoszony w Carnegie Mellon University, kwiecień 2004. dostęp 7 października, 2007.
- ↑ a b Culler i in., s. 124.
- ↑ Culler i in., s. 125.
- ↑ a b Patterson i Hennessy, s. 713.
- ↑ a b Patterson, Hennessy, s. 549.
- ↑ Patterson, Hennessy, s. 714.
- ↑ cotozajezyk (erlang.pl). [dostęp 2010-07-04]. [zarchiwizowane z tego adresu (19 sierpnia 2010)]. (pol.).
- ↑ What is clustering?. [dostęp 2008-05-16]. (ang.).
- ↑ Beowulf definition. PC Magazine. [dostęp 2008-05-16]. (ang.).
- ↑ Architecture share for 11/2007. [dostęp 2008-05-16]. [zarchiwizowane z tego adresu (21 kwietnia 2008)]. (ang.).
- ↑ Patterson i Hennessy, s. 537.
- ↑ MPP Definition. pcmag.com. [zarchiwizowane z tego adresu (2013-05-11)].. „PC Magazine”, dostęp 2 czerwca 2008.
- ↑ a b Michael R. D’Amour, CEO DRC Computer Corporation, Standard Reconfigurable Computing, Invited speaker at the University of Delaware, 28 lutego 2007.
- ↑ Sha’Kia Boggan, Daniel M. Pressel, GPUs: An Emerging Platform for General-Purpose Computation (PDF). ARL-SR-154, U.S. Army Research Lab. August 2007. Dostęp 7 listopada 2007.
- ↑ Oleg Maslennikov (2002), Systematic Generation of Executing Programs for Processor Elements in Parallel ASIC or FPGA-Based Systems and Their Transformation into VHDL-Descriptions of Processor Element Control Units, „Lecture Notes in Computer Science”, 2328/2002: s. 272.
- ↑ Y. Shimokawa, Y. Fuwa, N. Aramaki. A parallel ASIC VLSI neurocomputer for a large number of neurons and billion connections per second speed, IEEE International Joint Conference on Neural Networks, 18–21 listopada 1991. 3: s. 2162–2167.
- ↑ K.P. Acken, M.J. Irwin, R.M. Owens. A Parallel ASIC Architecture for Efficient Fractal Image Coding, „The Journal of VLSI Signal Processing”, lipiec 1998, 19(2):97–113(17).
- ↑ Andrew B. Kahng, Scoping the Problem of DFM in the Semiconductor Industry, University of California, San Diego, 21 czerwca 2004: „Future design for manufacturing (DFM) technology must reduce design [non-recoverable expenditure] cost and directly address manufacturing [non-recoverable expenditures] – the cost of a mask set and probe card – which is well over $1 million at the 90 nm technology node and creates a significant damper on semiconductor-based innovation.”.
- ↑ a b Patterson, Hennessy, s. 751.
- ↑ John Paul Shen, Mikko H. Lipasti, Modern Processor Design: Fundamentals of Superscalar Processors, McGraw-Hill Professional, 2005. ISBN 0-07-057064-7. s. 561: „However, the holy grail of such research – automated parallelization of serial programs – has yet to materialize. While automated parallelization of certain classes of algorithms has been demonstrated, such success has largely been limited to scientific and numeric applications with predictable flow control (e.g., nested loop structures with statically determined iteration counts) and statically analyzable memory access patterns. (e.g., walks over large multidimensional arrays of float-point data).”.
- ↑ Krste Asanovic, i in., The Landscape of Parallel Computing Research: A View from Berkeley (PDF). University of California, Berkeley. Raport techniczny numer UCB/EECS-2006-183, 18 grudnia 2006. Zobacz tabelę na stronach 17–19.
- ↑ L.F. Menabrea, Sketch of the Analytic Engine Invented by Charles Babbage, Bibliothèque Universelle de Genève, 1842, dostęp: 7 października 2007.
- ↑ a b Patterson i Hennessy, s. 753.
- ↑ Frank da Cruz: Columbia University Computing History: The IBM 704. Columbia University, 2003. [dostęp 2008-01-08]. (ang.).
- ↑ a b c d Gregory V. Wilson: The History of the Development of Parallel Computing. Virginia Tech/Norfolk State University, Interactive Learning with a Digital Library in Computer Science, 1994. [dostęp 2008-01-08]. (ang.).
- ↑ Gary Anthes: The Power of Parallelism. „Computerworld”, 2001-11-19. [dostęp 2008-01-08]. [zarchiwizowane z tego adresu (2008-01-31)].
- ↑ Gene Amdahl,Validity of the single processor approach to achieving large-scale computing capabilities. In: Proceedings of the American Federation Information Processing Society, vol. 30, 1967, 483–485.
- ↑ Patterson, Hennessy, s. 749.
- ↑ Patterson, Hennessy, s. 749–750: „Although successful in pushing several technologies useful in later projects, the ILLIAC IV failed as a computer. Costs escalated from the $8 million estimated in 1966 to $31 million by 1972, despite the construction of only a quarter of the planned machine ... It was perhaps the most infamous of supercomputers. The project started in 1965 and ran its first real application in 1976.”.
- ↑ John L. Hennessy, David A. Patterson, Computer Architecture: A Quantitative Approach, 3rd edition, 2002. Morgan Kaufmann, ISBN 1-55860-724-2, s. 43.
- ↑ J.M. Rabaey, Digital Integrated Circuits, Prentice Hall, 1996. ISBN 0-13-178609-1, s. 235.
- ↑ Laurie J. Flynn, Intel Halts Development of 2 New Microprocessors, „The New York Times”, 8 maja 2004, dostęp: 22 kwietnia 2008.
Linki zewnętrzne[edytuj | edytuj kod]
- Lawrence Livermore National Laboratory: Introduction to Parallel Computing
- Designing and Building Parallel Programs, by Ian Foster
- Internet Parallel Computing Archive. wotug.ukc.ac.uk. [zarchiwizowane z tego adresu (2002-10-12)].
- Parallel processing topic area at IEEE Distributed Computing Online. dsonline.computer.org. [zarchiwizowane z tego adresu (2011-09-28)].
- Parallel Computing Works Free On-line Book
- Frontiers of Supercomputing Free On-line Book Covering topics like algorithms and industrial applications


















