Trójkąt równoramienny

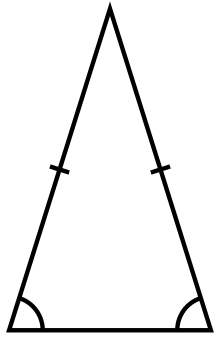
Trójkąt równoramienny – trójkąt o (co najmniej) dwóch bokach równej długości. Te dwa boki zwane są ramionami trójkąta, trzeci bok jego podstawą. Kąty przy podstawie są przystające a ich miara jest mniejsza od miary kąta prostego.

Trójkąt równoramienny posiada (co najmniej jedną) oś symetrii – przecina ona podstawę w połowie długości i przechodzi przez wierzchołek łączący ramiona. Oś symetrii pokrywa się z wysokością, środkową, dwusieczną i symetralną opuszczonymi na podstawę.

Szczególne przypadki trójkąta równoramiennego:

• trójkąt równoboczny – dowolne dwa boki można uznać za ramiona,
• równoramienny trójkąt prostokątny – kąt prosty może być jedynie między ramionami. Długość podstawy jest równa ${\sqrt {2}}$ długości ramienia.

Związki metryczne

Zależność między kątami

$2\alpha +\beta =\pi .$

Zależność między długością podstawy i ramienia:

$a^{2}=2b^{2}(1-\cos \beta ).$

Pole trójkąta równoramiennego:

$P=a^{2}{\frac {\cos \beta +1}{4\sin \beta }}={\tfrac {1}{2}}b^{2}\sin \beta ,$

gdzie:

$a$ – długość podstawy,

$b$ – długość ramienia,

$\beta$ – miara kąta przeciwległego do $a,$ czyli kąta między ramionami

$\alpha$ – miara kąta przy podstawie

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Isosceles Triangle, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2023-06-01].