Romb

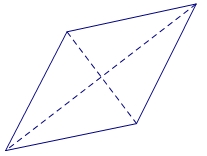
Rysunek rombu z oznaczeniami

Romb (rzadziej ukośnik) – w geometrii czworokąt (wypukły) o bokach równej długości; każdy romb jest równoległobokiem, zaś szczególnym jego przypadkiem (o wszystkich kątach prostych) jest kwadrat.

Wzory

Jeżeli $a$ oznacza długość boku rombu, a $h$ jego wysokość (tzn. odległość między dwoma równoległymi bokami), zaś $d, f$ to długości odpowiednio krótszej i dłuższej przekątnej rombu, podczas gdy $\alpha$ jest miarą kąta ostrego albo prostego pomiędzy bokami rombu, to prawdziwe są poniższe wzory:

• pole powierzchni,

  $P = ah = a^2 \sin \alpha = \tfrac{1}{2} df,$

• obwód,

  $O = 4a,$

• promień okręgu wpisanego,

  $r = \tfrac{1}{2} a \sin \alpha,$

• długości przekątnych wyrażone za pomocą długości boków,

  $d = 2a \sin \tfrac{\alpha}{2},$

  $f = 2a \cos \tfrac{\alpha}{2}.$

Własności

• Suma miar wszystkich kątów wewnętrznych wynosi $2\pi$ (360°), a suma miar dwóch sąsiednich kątów wewnętrznych wynosi $\pi$ (180°).
• Przekątne przecinają się pod kątem prostym dzieląc romb na cztery przystające trójkąty prostokątne.
• Punkt przecięcia przekątnych rombu dzieli każdą z nich na połowy wyznaczając środek okręgu wpisanego będąc przy tym środkiem symetrii rombu.
• Przekątne pokrywają się z dwusiecznymi kątów oraz osiami symetrii rombu.

Zobacz też

• równoległobok,
• deltoid,
• kwadrat,
• prostokąt.

Linki zewnętrzne

• Romb w MathWorld.com
• Geometria Jana Zydlera: Rozdział 21. Równoległoboki i ich własności. Trapez