Oktawy Cayleya
Oktawy Cayleya, oktoniony (łac. octo – osiem), liczby Cayleya – rozszerzenie kwaternionów stanowiące niełączną algebrę. Opisało ją niezależnie dwóch matematyków: John T. Graves w roku 1843 i Arthur Cayley w roku 1845.
Oktoniony są trzecią z kolei po liczbach zespolonych i kwaternionach algebrą powstałą przez zastosowanie konstrukcji Cayleya-Dicksona do liczb rzeczywistych.
Są algebrą 8-wymiarowej przestrzeni liniowej nad ciałem liczb rzeczywistych. Z tego też powodu mogą być traktowane jako ośmioelementowe ciągi liczb rzeczywistych. Oktawa jest kombinacją liniową jedynki i 7 jednostek urojonych tworzących bazę standardową przestrzeni: 1, e1, e2, e3, e4, e5, e6 i e7. Gdzie e1...e7 podniesione do kwadratu dają −1. Działanie dodawania na oktawach jest równoważne dodawaniu wektorów 8-wymiarowej przestrzeni, natomiast działanie mnożenia definiuje poniższa tabela:
| · | 1 | e1 | e2 | e3 | e4 | e5 | e6 | e7 |
| 1 | 1 | e1 | e2 | e3 | e4 | e5 | e6 | e7 |
| e1 | e1 | −1 | e4 | e7 | –e2 | e6 | –e5 | –e3 |
| e2 | e2 | –e4 | −1 | e5 | e1 | –e3 | e7 | –e6 |
| e3 | e3 | –e7 | –e5 | −1 | e6 | e2 | –e4 | e1 |
| e4 | e4 | e2 | –e1 | –e6 | −1 | e7 | e3 | –e5 |
| e5 | e5 | –e6 | e3 | –e2 | –e7 | −1 | e1 | e4 |
| e6 | e6 | e5 | –e7 | e4 | –e3 | –e1 | −1 | e2 |
| e7 | e7 | e3 | e6 | –e1 | e5 | –e4 | –e2 | −1 |
Kolejność w mnożeniu to wiersze (ei) – kolumny (ej). Stąd też:
- dla
tu działania oznaczają:
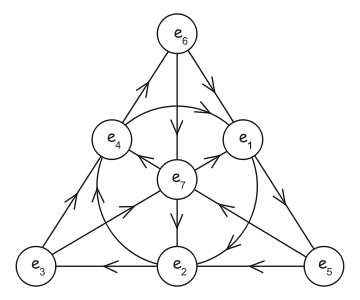
Obrazek przedstawia metodę mnożenia oktonionów. Porównanie z tabelką u góry może pomóc w jej zrozumieniu i zapamiętaniu.
Oktawy stanowią jedyną algebrę skończonego wymiaru nad ciałem liczb rzeczywistych z wykonalnym dzieleniem, w której mnożenie nie jest łączne, ale jest alternatywne (tj. łączne w algebrze tworzonej przez każde dwa z jej elementów).
Oktawy Cayleya zawierają w sobie algebry izomorficzne z:
Z drugiej strony można zanurzyć w następujących algebrach:
Zobacz też[edytuj | edytuj kod]
Linki zewnętrzne[edytuj | edytuj kod]
- Eric W. Weisstein, Octonion, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2024-03-07].
- The Octonions – artykuł Johna C. Baeza