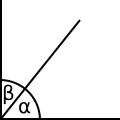
Kąt
Kąt – obszar powstały z rozcięcia płaszczyzny przez sumę dwóch różnych półprostych o wspólnym początku, wraz z tymi półprostymi[1]. Półproste nazywane są ramionami kąta, wspólny początek półprostych nazywany jest wierzchołkiem kąta[2].
Kąt można też zdefiniować jako część wspólną lub jako sumę dwóch półpłaszczyzn z brzegiem wyznaczonych przez dwie nierównoległe proste. Wówczas należy dodatkowo zdefiniować „kąt pełny” jako całą płaszczyznę, „kąt półpełny” jako półpłaszczyznę oraz „kąt zerowy” jako półprostą.
Gdy kąt obejmuje całą płaszczyznę (w przypadku „kąta pełnego”) pomocne bywa wyróżnienie na płaszczyźnie półprostej pełniącej rolę ramion i z jej początkiem jako wierzchołkiem kąta. Podobnie gdy ramiona dopełniają się do prostej (dając „kąt półpełny”), wyróżnia się czasem wspólny początek półprostych, tj. ustalony punkt powstałej prostej, jako wierzchołek.
- W artykule opisano kąt płaski na płaszczyźnie euklidesowej z uogólnieniami w osobnej sekcji.
Miara kąta[edytuj | edytuj kod]
Kąt liczbowo wyrażony w jednostkach kąta nazywa się miarą kąta. Często, niezbyt precyzyjnie, kątem nazywa się jego miarę.
Kąt skierowany[edytuj | edytuj kod]
Kątem obrotu nazywa się miarę kąta (skierowanego) między dowolną prostą przechodzącą przez środek (punkt stały) obrotu a prostą będącą jej obrazem (wspomniane dwie proste przecinają się we wspomnianym środku wyznaczając kąt w powyższym sensie).
Klasyfikacja[edytuj | edytuj kod]
Kąty można też klasyfikować ze względu na pojęcia zawierania (kąty zerowy, półpełny i pełny), wypukłości (kąty wypukły i wklęsły), bądź prostopadłości lub przystawania (kąt prosty; kąty ostry i rozwarty – z zawieraniem). Ponieważ dwa kąty płaskie o równej tej samej mierze są przystające, to klasyfikacji kątów można dokonać grupując je również względem ustalonego zakresu ich miar (niżej używane będą miara łukowa wraz z miarą stopniową podaną w nawiasie):
| nazwa kąta | opis | wzór | |
|---|---|---|---|
| wypukły | kąt będący figurą wypukłą; miara takiego kąta jest mniejsza lub równa π rad (lub 180°) albo równa 2π rad (lub 360°); czasem ta nierówność jest ostra – kąt wypukły musi być mniejszy od półpełnego[3]; | α < 180° | |
| zerowy | kąt utworzony przez dwie półproste pokrywające się, a tym samym im równy; jego miara jest równa 0 rad (lub 0°); | α = 0° | |
| ostry | kąt ściśle zawierający się w pewnym kącie prostym; ma miarę większą od 0 rad (lub 0°), lecz mniejszą od π/2 rad (lub 90°)[4]; | 0° < α < 90° | |
| prosty | kąt przystający do kąta mającego z nim wspólne jedno tylko ramię, podczas gdy pozostałe ramiona tworzą prostą[a]; jego miara wynosi π/2 rad (lub 90°); | α = 90° | |
| rozwarty | kąt ściśle zawarty w pewnym kącie półpełnym, lecz niebędący ani ostrym, ani prostym; ma miarę większą niż π/2 rad (lub 90°), lecz mniejszą niż π rad (lub 180°)[5]; | 90° < α < 180° | |
| półpełny | każdy z dwu kątów utworzonych przez dwie półproste uzupełniające się do prostej; jego miara wynosi π rad (lub 180°)[6]; | α = 180° | |
| wklęsły | kąt, który nie jest wypukły; miara takiego kąta jest większa niż π rad (lub 180°), lecz mniejsza niż 2π rad (lub 360°)[7]. | 180° < α < 360° | |
| pełny | kąt utworzony przez dwie półproste pokrywające się i równy całej płaszczyźnie; jego miara jest równa 2π rad (lub 360°)[8]; | α = 360° | |
Wyjąwszy przypadek, gdy ramiona kąta uzupełniają się do prostej (oba kąty są wtedy półpełne) lub pokrywają się (jeden z kątów jest wtedy zerowy, a drugi pełny), jeden z kątów można jednoznacznie zidentyfikować jako wypukły, drugi zaś jako wklęsły (w przeciwnym przypadku oba są wypukłe); czasem możliwe jest też wyróżnienie wśród nich kąta rozwartego bądź ostrego.
Kąty wyznaczane przez proste[edytuj | edytuj kod]
-
Para kątów przyległych
-
Kąty dopełniające
-
Kąty są wierzchołkowe
-
Kąty naprzemianległe wewnętrzne
-
Kąty naprzemianległe zewnętrzne

Dowolne dwie nierównoległe proste na płaszczyźnie wyznaczają dwie pary kątów: pary mające wspólne ramię nazywa się kątami przyległymi, z kolei pary mające wspólny wyłącznie wierzchołek nazywa się wierzchołkowymi. Suma miar kątów przyległych jest równa mierze kąta półpełnego, a miary kątów wierzchołkowych są równe. Kąty mające jedno wspólne ramię, pozostałe zaś leżące pod kątem prostym, nazywa się kątami dopełniającymi; suma miar kątów dopełniających jest więc równa mierze kąta prostego[b].
Dowolne dwie proste przecięte (nierównoległą do żadnej z nich) trzecią prostą nazywaną sieczną lub transwersalą (prostą transwersalną) wyznaczają łącznie osiem kątów wokół dwóch punktów przecięcia (por. rys. obok). Pary kątów o ramionach na ustalonej prostej lub są przyległe bądź wierzchołkowe (odpowiednio: pary różnej lub tej samej parzystości z kątów bądź ).
Cztery kąty leżące między prostymi nazywa się wewnętrznymi a pozostałe cztery – zewnętrznymi pary kątów nieprzyległych leżących po jednej stronie prostej nazywa się jednostronnymi (różnokolorowe pary z kątów bądź z kątów ), z kolei pary kątów nieprzyległych branych z różnych stron tej prostej nazywa się naprzemianległymi[c] (różnokolorowe pary z kątów bądź z kątów ). W ten sposób wyróżnia się po dwie pary kątów:
- jednostronnych wewnętrznych ( oraz ),
- jednostronnych zewnętrznych ( oraz ),
- naprzemianległych wewnętrznych ( oraz ),
- naprzemianległych zewnętrznych ( oraz ).
Cztery pary nieprzyległych kątów jednostronnych, które nie są wewnętrzne ani zewnętrzne, nazywa się odpowiadającymi[c] ( oraz ).
- Twierdzenie
- Proste przecięte transwersalą są równoległe wtedy i tylko wtedy, gdy choć jedna para kątów wierzchołkowych bądź odpowiadających jest przystająca (równej miary).
Funkcje trygonometryczne kątów dopełniających („komplementarnych”[d]) dany kąt nazywa się kofunkcjami: sinus kąta dopełniającego nazywa się kosinusem danego kąta, podobnie ma się rzecz z tangensem i kotangensem oraz sekansem i kosekansem. Kofunkcją dla kofunkcji danego kąta jest funkcja tego kąta, gdyż kątem dopełniającym do kąta dopełniającego dany kąt jest on sam – dlatego kofunkcją dla kosinusa, kotangensa, czy kosekansa są odpowiednio sinus, tangens i sekans. Analogiczne uwagi obowiązują dla funkcji cyklometrycznych, hiperbolicznych oraz area.
Kąty związane z okręgiem[edytuj | edytuj kod]

Dowolny kąt, który wycina z okręgu ustalony łuk, nazywa się opartym na tym łuku[e]. Kąt, którego wierzchołek leży w środku danego okręgu, nazywa się środkowym; ponieważ okrąg jest zbiorem punktów równoodległych od jego środka, to „ilość” punktów (długość łuku) wspólna z danym kątem środkowym w stosunku do ich odległości od środka opisuje „rozmiar” tego kąta – obserwacja ta została wykorzystana do określenia miary łukowej dowolnego kąta, jak przedstawiono to wyżej. Kątem wpisanym w ustalony okrąg nazywa się dowolny kąt, którego wierzchołek leży na tym okręgu, a jego ramiona są zarazem jego siecznymi, z kolei kąt dopisany do okręgu w wybranym jego punkcie, to kąt ostry o wierzchołku w tymże punkcie, którego jedno ramię jest sieczną, a drugie – styczną wspomnianego okręgu; można go traktować jako zdegenerowany przypadek kąta wpisanego, w którym jedna z siecznych staje się styczną.
- Twierdzenie o kątach wpisanych
- Miary kątów wpisanych opartych na tym samym łuku są równe.
- Twierdzenie o kątach środkowym i wpisanym
- Miara kąta środkowego jest dwa razy większa od miary kąta wpisanego opartych na tym samym łuku.
- Twierdzenie o stycznej i siecznej
- Miara kąta dopisanego wycinającego dany łuk jest równa mierze kąta wpisanego opartego na tym łuku.
Uogólnienia[edytuj | edytuj kod]
Definiuje się również kąty między innymi płaskimi figurami geometrycznymi niż (pół)proste: tego samego rodzaju, np. wektorami (analogicznie), krzywymi (w danym punkcie, w tym okręgami: jako kąt między stycznymi, o ile istnieją i są wyznaczone jednoznacznie).
Rozpatruje się także pojęcie kąta w przestrzeni trójwymiarowej i wielowymiarowej, np. między płaszczyznami (definiowane np. za pomocą wektorów normalnych), czy prostą i płaszczyzną (jako kąt między prostą a jej rzutem prostopadłym na płaszczyznę).
Zobacz też[edytuj | edytuj kod]
Uwagi[edytuj | edytuj kod]
- ↑ Zgodnie z definicjami w kolejnej sekcji: kąt przystający do kąta doń przyległego.
- ↑ W polskiej nomenklaturze brak jest terminów opisujących związek między innymi parami kątów, obecnych jednak w innych językach, np. kątów o wspólnym jednym i tylko jednym ramieniu (ang. adjacent angles, „kąty sąsiednie/sąsiadujące, przylegające”; hiszp. ángulos consecutivos, „następujące, sąsiadujące”), czy mających wspólne dokładnie dwa ramiona (ang. explementary angles, „kąty wypełniające”; ang. conjugate angles, hiszp. ángulos conjugados, „kąty sprzężone”). Suma miar kątów mających dokładnie jedno wspólne ramię jest równa mierze kąta wyznaczonego przez pozostałe ramiona tych kątów; suma miar kątów o dwóch wspólnych ramionach jest równa mierze kąta pełnego.
- ↑ a b Nieprzyległe kąty naprzemianległe, które nie są wewnętrzne ani zewnętrzne, w przeciwieństwie do nieprzyległych jednostronnych niewewnętrznych i niezewnętrznych nie mają swojej ustalonej nazwy (z tego też powodu zwykle nie zalicza się ich do kątów naprzemianległych).
- ↑ Łac. complementum, „dopełnienie”; od complēre, „wypełnić, uzupełnić”, od com-, „wraz, z, razem; dogłębnie” + plēre, „napełniać”; gr. πλήρης plērēs, „pełny”, od πλήθειν plēthein, „być pełnym”.
- ↑ Wskazanie końców łuku jest niewystarczające, dla ustalonych dwóch ramion dany kąt można wybrać na dwa sposoby – do wyróżnienia jednego z nich, oprócz posiłkowania się miarą lub inną własnością kąta możliwe jest też doprecyzowanie łuku, który dany kąt wycina w okręgu: do tego celu wykorzystuje się również pojęcia łuku skierowanego/zorientowanego (zob. relacja leżenia między) lub kąta skierowanego/zorientowanego.
Przypisy[edytuj | edytuj kod]
- ↑ Encyklopedia dla wszystkich, Warszawa: WNT, 2000, s. 135, ISBN 83-204-2334-1.
- ↑ kąt, [w:] Encyklopedia PWN [dostęp 2021-10-01].
- ↑ kąt wypukły, [w:] Encyklopedia PWN [dostęp 2021-10-16].
- ↑ kąt ostry, [w:] Encyklopedia PWN [dostęp 2021-10-16].
- ↑ kąt rozwarty, [w:] Encyklopedia PWN [dostęp 2021-10-16].
- ↑ kąt półpełny, [w:] Encyklopedia PWN [dostęp 2021-10-16].
- ↑ kąt wklęsły, [w:] Encyklopedia PWN [dostęp 2021-10-16].
- ↑ kąt pełny, [w:] Encyklopedia PWN [dostęp 2021-10-16].
Bibliografia[edytuj | edytuj kod]
- „Encyklopedia Matematyka”, wyd. Greg, ISBN 978-83-7517-015-3 (kąt skierowany)