Funkcja sigmoidalna

Krzywa logistyczna

Wykres funkcji błędu

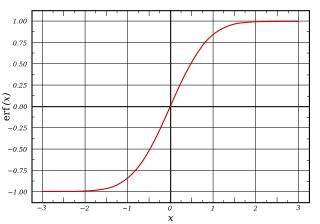
Funkcja sigmoidalna – dowolna funkcja matematyczna, której wykres ma charakterystyczny kształt litery S.

Typowym przykładem funkcji sigmoidalnej jest funkcja logistyczna pokazana na pierwszym rysunku i opisana wzorem:

$\sigma (x)={\frac {1}{1+e^{-x}}}={\frac {e^{x}}{1+e^{x}}}=1-\sigma (-x).$

Inne przykłady funkcji sigmoidalnych przytoczono poniżej. W niektórych dziedzinach, zwłaszcza w kontekście sztucznych sieci neuronowych, termin „funkcja sigmoidalna” jest używany jako synonim funkcji logistycznej.

Dziedziną funkcji sigmoidalnej jest zbiór wszystkich liczb rzeczywistych. Wartości funkcji zwykle monotonicznie rosną (ale mogą również maleć). Typowym zbiorem wartości funkcji sigmoidalnych jest przedział od 0 do 1 lub od -1 do 1.

Wiele funkcji sigmoidalnych może pełnić rolę funkcji aktywacji sztucznych neuronów w sieciach neuronowych, są to na przykład funkcja logistyczna i tangens hiperboliczny. Krzywe sigmoidalne są również powszechne w statystyce jako dystrybuanty rozkładów prawdopodobieństwa (przyjmujące wartości z przedziału od 0 do 1); przykładem może być całka funkcji gęstości rozkładu logistycznego, rozkładu normalnego czy rozkładu t -Studenta.

Definicja

Funkcja sigmoidalna jest ograniczoną, różniczkowalną funkcją rzeczywistą, która jest zdefiniowana dla wszystkich rzeczywistych argumentów, ma nieujemną pochodną w każdym punkcie oraz pojedynczy punkt przegięcia.

Własności

Ogólnie rzecz biorąc, funkcja sigmoidalna jest monotoniczna i jej pierwsza pochodna ma kształt krzywej dzwonowej. I odwrotnie: całka dowolnej ciągłej, nieujemnej funkcji z wykresem w kształcie dzwonu (z jednym lokalnym maksimum i bez lokalnych minimów) będzie sigmoidalna. Zatem dystrybuanty wielu powszechnie wykorzystywanych rozkładów prawdopodobieństwa są sigmoidalne. Sigmoidalna jest funkcja błędu, która jest powiązana z dystrybuantą rozkładu normalnego i funkcja arcus tangens powiązana z dystrybuantą rozkładu Cauchy’ego .

Funkcja sigmoidalna jest ograniczona parą asymptot poziomych dla $x\rightarrow \pm \infty$ .

Rosnąca funkcja sigmoidalna jest wypukła dla wartości poniżej punktu przegięcia i wklęsła dla wartości powyżej tego punktu. W wielu przykładach punktem przegięcia jest 0.

Przykłady

Porównanie niektórych funkcji sigmoidalnych. Na rysunku wszystkie funkcje są znormalizowane w taki sposób, że ich nachylenie w początku układu współrzędnych wynosi 1.

• funkcja logistyczna:$$f(x)={\frac {1}{1+e^{-x}}}$$
• tangens hiperboliczny (przesunięta i przeskalowana wersja funkcji logistycznej): $$f(x)=\tanh x={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$$
• funkcja arcus tangens:$$f(x)=\arctan x$$
• funkcja Gudermanna:$$f(x)=\operatorname {gd} (x)=\int _{0}^{x}{\frac {dt}{\cosh t}}=2\arctan \left(\tanh \left({\frac {x}{2}}\right)\right)$$
• funkcja błędu:$$f(x)=\operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,dt$$
• uogólniona funkcja logistyczna:$$f(x)=\left(1+e^{-x}\right)^{-\alpha },\quad \alpha >0$$
• funkcja smoothstep:$$f(x)={\begin{cases}{\displaystyle \left(\int _{0}^{1}\left(1-u^{2}\right)^{N}du\right)^{-1}\int _{0}^{x}\left(1-u^{2}\right)^{N}\ du},&|x|\leq 1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\quad N\in \mathbb {Z} \geq 1$$
• niektóre funkcje algebraiczne, np.:$$f(x)={\frac {x}{\sqrt {1+x^{2}}}}$$i w bardziej ogólnej formie:$$f(x)={\frac {x}{\left(1+|x|^{k}\right)^{1/k}}}$$
• funkcja płynnego przejścia znormalizowana do (-1,1):$${\begin{aligned}f(x)&={\begin{cases}{\displaystyle {\frac {2}{1+e^{-2m{\frac {x}{1-x^{2}}}}}}-1},&|x|<1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\\&={\begin{cases}{\displaystyle \tanh \left(m{\frac {x}{1-x^{2}}}\right)},&|x|<1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\end{aligned}}$$,

gdzie $m$ jest parametrem sterującym nachyleniem wykresu w pobliżu $x=0$ ($m$ musi być większe lub równe ${\sqrt {3}}$, ponieważ każda mniejsza wartość prowadzi do krzywej z więcej niż jednym punktem przegięcia, a zatem krzywej nie będącej prawdziwą sigmoidą). Funkcja ta jest nietypowa, ponieważ osiąga wartości graniczne -1 i 1: jej wartość wynosi -1 dla wszystkich $x\leq -1$ i 1 dla wszystkich $x\geq 1$ . Niemniej jednak jest ona gładka (nieskończenie różniczkowalna, $C^{\infty }$) wszędzie, w tym w $x=\pm 1$ .

Z dokładnością do przesunięcia i skalowania wiele funkcji sigmoidalnych to szczególne przypadki funkcji:$$f(x)=\varphi (\varphi (x,\beta ),\alpha ),$$ gdzie $$\varphi (x,\lambda )={\begin{cases}(1-\lambda x)^{1/\lambda }&\lambda \neq 0\\e^{-x}&\lambda =0\\\end{cases}}$$ jest odwrotnością ujemnego przekształcenia Boxa-Coxa, zaś $\alpha <1$ i $\beta <1$ są parametrami kształtu.

Zastosowanie

Odwrócona logistyczna krzywa S do modelowania zależności między plonem pszenicy a zasoleniem gleby

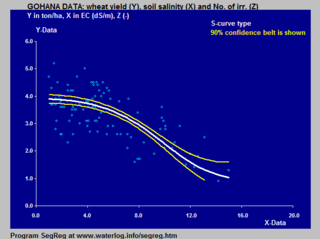
Krzywe sigmoidalne wykorzystuje się w charakterze funkcji aktywacji w sztucznych sieciach neuronowych.

Wiele naturalnych procesów, takich jak krzywe uczenia się w złożonych systemach, wykazuje na początku niewielki wzrost, który z czasem przyspiesza i osiąga punkt kulminacyjny. Gdy brakuje konkretnego modelu matematycznego opisującego proces, często stosuje się funkcję sigmoidalną.

Model van Genuchtena-Gupty opiera się na odwróconej krzywej S i stosuje się go do opisu zależności plonów od zasolenia gleby. Przykłady zastosowania logistycznej krzywej S do reakcji plonów roślin uprawnych (pszenicy) zarówno na zasolenie gleby, jak i głębokość zwierciadła wody w glebie pokazano w modelowaniu reakcji upraw w rolnictwie.

W przetwarzaniu sygnałów dźwiękowych funkcje sigmoidalne służą jako funkcje przejścia modułu kształtowania fali w celu emulacji dźwięku przesterowania obwodów analogowych.

W biochemii i farmakologii równania Hilla i Hilla–Langmuira są funkcjami sigmoidalnymi.

W grafice komputerowej i renderowaniu w czasie rzeczywistym niektóre funkcje sigmoidalne służą do płynnego łączenia kolorów lub obiektów geometrycznych pomiędzy dwiema wartościami, bez widocznych nieciągłości.

Krzywe miareczkowania pomiędzy mocnymi kwasami i mocnymi zasadami mają kształt sigmoidalny ze względu na logarytmiczny charakter skali pH.

Zobacz też

• Funkcja schodkowa
• Funkcja signum
• Funkcja skokowa Heaviside’a
• Regresja logistyczna
• Funkcja logitowa
• Funkcja softmax
• Funkcja swish
• Rozkład Weibulla
• Statystyka Fermiego-Diraca