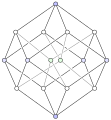
Dwunastościan rombowy

Dwunastościan rombowy
(Kliknij, aby zobaczyć animowany model)
Typ	Wielościan Catalana
Ściana	romb
Liczba ścian	12
Liczba krawędzi	24
Liczba wierzchołków	14 = 6 + 8
Wielościan dualny	Sześcio-ośmiościan

Dwunastościan rombowy – bryła przestrzenna mająca 12 ścian, 14 wierzchołków i 24 krawędzie. Wszystkie ściany są przystającymi rombami o następującej własności: stosunek długości przekątnych jest równy $\sqrt 2$. W każdym wierzchołku spotykają się 3 lub 4 ściany. W ośmiu wierzchołkach stykają się kątami rozwartymi 3 romby, zaś w pozostałych sześciu wierzchołkach stykają się kątami ostrymi 4 romby. Kąt ostry każdej ściany jest równy $\arccos {\frac {1}{3}} \approx 70^\circ$. Krótsze przekątne wszystkich ścian są krawędziami sześcianu.

Dwunastościan rombowy jest dualny z wielościanem archimedesowym zwanym sześcio-ośmiościanem i dlatego grupa symetrii bryły działa przechodnio na zbiorze ścian. Przechodniość ta oznacza, że dla dwóch ścian A i B istnieje obrót lub symetria przekształcające bryłę na siebie, a ścianę A na ścianę B.
Grupa symetrii dwunastościanu rombowego działa także przechodnio na zbiorze krawędzi tej bryły.

Rozmiary bryły

Dwunastościan rombowy (czarne krawędzie) i dualny z nim sześcio-ośmiościan (zielone krawędzie).

Jeśli długość krawędzi dwunastościanu rombowego jest równa $a\;$, to promień sfery wpisanej w dwunastościan rombowy jest równy

$r_i = a \sqrt{\frac{2}{3}} \approx 0.8164965809 \cdot a,$

promień sfery przechodzącej przez środki krawędzi jest równy

$r_m = a \frac23 \sqrt{2} \approx 0.94280904158 \cdot a,$.

a promień sfery opisanej jest równy

$r_o = a \frac2{\sqrt{3}} \approx 1.154700538 \cdot a$.

Pole i objętość

Pole powierzchni $S\;$ i objętość $V\;$ dwunastościanu rombowego o krawędzi $a\;$ są równe:

$S = 8\sqrt{2}a^2 \approx 11.3137085a^2$

$V = \frac{16}{9} \sqrt{3}a^3 \approx 3.07920144a^3$

Występowanie w przyrodzie

Kryształ granatu

Niektóre kryształy występujące w przyrodzie przybierają formę dwunastościanu rombowego. Są to przede wszystkim kryształy granatu, ale tę formę przyjmuje wiele innych minerałów, na przykład magnetyt, sodalit, spinel i sfaleryt.

Pszczoły używają geometrii tej bryły do tworzenia plastrów miodu, których komórki są graniastosłupami prawidłowymi, sześciokątnymi zamkniętymi połówkami dwunastościanu rombowego.

Jak można sobie wyobrazić kształt dwunastościanu rombowego

Wypełnienie przestrzeni przystającymi dwunastościanami rombowymi.

Krótkie przekątne rombów, i wierzchołki, w których romby stykają się kątami rozwartymi są krawędziami i wierzchołkami sześcianu o objętości równej połowie objętości samego dwunastościanu. Długie przekątne rombów, i wierzchołki, w których romby stykają się kątami ostrymi, są krawędziami i wierzchołkami ośmiościanu foremnego.

Ten dwunastościan można skonstruować, wychodząc z sześcianu, w następujący sposób: budujemy ostrosłup, którego podstawą jest ściana, a wierzchołkiem lustrzane odbicie środka sześcianu w płaszczyźnie ściany, powiększając sześcian o ten ostrosłup; powtarzając to dla wszystkich ścian uzyskamy dwunastościan rombowy, a użyte ostrosłupy będą składać się na kompletny sześcian - więc objętość dwunastościanu będzie 2 razy większa.

Powyższe wywody można zilustrować w układzie współrzędnych w przestrzeni:

• Punkty (± 1, ± 1, ± 1) są wierzchołkami sześcianu o ścianach rozpiętych na sześciu czwórkach punktów: {(1, ± 1, ± 1)}, {(- 1, ± 1, ± 1)}, {(± 1, 1, ± 1)}, {(± 1, - 1, ± 1)}, {(± 1, ± 1, 1)}, {(± 1, ± 1, - 1)}.
• Do powyższych 8 punktów dołączamy 6 następnych: (± 2, 0, 0), (0, ± 2, 0), (0, 0, ± 2). Są one obrazami początku układu współrzędnych O w symetrii względem poszczególnych ścian, np. punkt (- 2, 0, 0) jest obrazem O w symetrii względem ściany (- 1, ± 1, ± 1), a punkt (2, 0, 0) - w symetrii względem ściany (1, ± 1, ± 1).
• 14 wyżej wymienionych punktów jest wierzchołkami dwunastościanu rombowego.

Takie dwunastościany mogą wypełnić przestrzeń - żeby skonstruować taki układ wystarczy wyjść z układu sześcianów wypełniających przestrzeń, usunąć z nich co drugi, tak aby z każdych dwóch o wspólnej ścianie jeden został usunięty, i pozostałych użyć do konstrukcji dwunastościanów, odbijając ich środki względem sześciu ścian.

Wielościany pokrewne

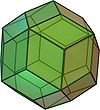
Dwunastościan rombowy jest elementem ciągu wielościanów rombowych i parkietaży, których grupa symetrii jest [n, 3] grupą Coxetera. Sześcian (geometria) może bowiem być uważany za sześciościan rombowy, gdzie romby są kwadratami.

Wielościan			Parkietaż euklidesowy	Parkietaż hiperboliczny
[3, 3]	[4, 3]	[5, 3]	[6, 3]	[7, 3]	[8, 3]
Sześcian	Dwunastościan rombowy	Trzydziestościan rombowy

Związki z bryłami czterowymiarowymi

Czterowymiarowym odpowiednikiem dwunastościanu rombowego jest 24-komórka) (jest to komórka foremna).

Jej wierzchołkami są:

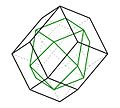
• 16 wierzchołków czterowymiarowego odpowiednika sześcianu - 8-komórki: (± 1, ± 1, ± 1, ± 1). Jej 3-wymiarowymi ścianami są sześciany rozpięte na ośmiu ósemkach punktów: {(1, ± 1, ± 1, ± 1)}, {(- 1, ± 1, ± 1, ± 1)}, {(± 1, 1, ± 1, ± 1)}, {(± 1, - 1, ± 1, ± 1)}, {(± 1, ± 1, 1, ± 1)}, {(± 1, ± 1, - 1, ± 1)}, {(± 1, ± 1, ± 1, 1)}, {(± 1, ± 1, ± 1, - 1)}.
• Ponadto wierzchołkami 24-komórki są obrazy środka O układu współrzędnych w ośmiu ścianach: (± 2, 0, 0, 0), (0, ± 2, 0, 0), (0, 0, ± 2, 0), (0, 0, 0, ± 2).

Przekrój 24-komórki przestrzenią 3-wymiarową prostopadłą do największej przekątnej w jej środku jest dwunastościanem rombowym. Wynika to z powyższych opisów obu figur geometrycznych w układzie współrzędnych kartezjańskich.

Dwunastościan jest także otoczką wypukłą rzutu prostokątnego 8-komórki wzdłuż wielkiej przekątnej. Ilustruje to rysunek poniżej. Rzut zielonych punktów jest wtedy środkiem dwunastościanu.

• 

  24-komórka

• 

  Dwunastościan rombowy i 8-komórka

Bibliografia

1. The Geometrical Foundation of Natural Structure (Section 3-9)
2. Magnus Wenninger: Dual Models. MR730208.
3. The thirteen semiregular convex polyhedra and their duals, Page 19, Rhombic dodecahedron
4. The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 285, Rhombic dodecahedron )
5. Marcel Berger: Géométrie (tłum. na jęz. ros.). Москва: Мир, 1984.
6. Hilbert D., Cohn-Vossen S.: Geometria poglądowa (tłum. z jęz. niem.). Warszawa: PWN, 1956.

Linki zewnętrzne

• Virtual Reality Polyhedra – Encyklopedia wielościanów.

Modele komputerowe

• Rhombic Dodecahedron -- interaktywne modele 3-wymiarowe.
• Relating a Rhombic Triacontahedron and a Rhombic Dodecahedron (Sándor Kabai)
• Rhombic Dodecahedron 5-Compound (Sándor Kabai)
• Rhombic Dodecahedron 5-Compound (Sándor Kabai)

Projekty papierowe

• Rhombic Dodecahedron Calendar – kalendarz w postaci dwunastościanu rombowego (bez użycia kleju)
• Another Rhombic Dodecahedron Calendar

Zastosowania praktyczne

• Archimede Institute - projekty przedmiotów w kształcie dwunastościanu rombowego.