Układ krystalograficzny
Układ krystalograficzny – system klasyfikacji kryształów ze względu na układ wewnętrzny cząsteczek w sieci krystalicznej. Układ krystalograficzny definiuje się także jako zespół klas symetrii, których elementy powodują jednakowe ograniczenia stałych sieciowych komórki elementarnej sieci przestrzennej[1]. System wyróżnia siedem układów, w których wyróżnia się 32 klasy krystalograficzne.
Ogólne informacje[edytuj | edytuj kod]
Uznany podział wyróżnia sześć układów krystalograficznych (regularny, heksagonalny, tetragonalny, rombowy, jednoskośny i trójskośny). Ze względów tradycjonalnych można spotkać podziały z dodatkowym układem trygonalnym, który w rzeczywistości jest komórką romboedryczną układu heksagonalnego[1]. Układ cząstek wynika po części ze struktury chemicznej cząsteczki. Większość kryształów przyjmuje formę regularnego wielościanu. Zewnętrzny kształt kryształu (monokryształu) jest odzwierciedleniem jego struktury wewnętrznej. Wewnątrz kryształu atomy, jony i cząsteczki są uporządkowane przestrzennie w określony, regularny sposób.
Elementami symetrii budowy kryształów są:
Wyróżnia się następujące układy krystalograficzne[edytuj | edytuj kod]
- układ regularny, np. sól kamienna, diament, magnetyt, spinel
- układ tetragonalny, np. kasyteryt, cyrkon, wezuwian, szelit, wulfenit
- układ heksagonalny, np. beryl, pirotyn, apatyt, cynkit, nefelin, grafit
- układ trygonalny, np. romboedr, skalenoedr, kalcyt, korund, kwarc
- układ rombowy, np. siarka, baryt, oliwin, struwit, hemimorfit
- układ jednoskośny, np. wolframit, gips, tytanit, augit, ortoklaz
- układ trójskośny, np. chalkantyt, dysten = cyanit, aksynit, rodonit, albit
Istnieją substancje niemające struktury krystalicznej – amorficzne (bezpostaciowe), zwane też szkłami, np. opal. Mimo iż nie są minerałami, są przedmiotem badań mineralogii. Nazywa się je mineraloidami.
Z reguły jednemu związkowi chemicznemu odpowiada jedna klasa krystalograficzna, chociaż niektóre minerały o jednakowym składzie chemicznym mają różną budowę wewnętrzną i należą do różnych klas krystalograficznych. Zjawisko to definiuje się jako polimorfizm.
Przykładowe formy polimorficzne (alotropowe):
- (dla węgla) diament i grafit
- kalcyt i aragonit
- piryt i markasyt
- kwarc, trydymit i krystobalit
- rutyl, anataz i brukit
Charakterystyka układów[edytuj | edytuj kod]
| Układ | Jednostki osiowe | Kąty między osiami |
|---|---|---|
| regularny | a = b = c | α = β = γ = 90° |
| tetragonalny | a = b ≠ c | α = β = γ = 90° |
| rombowy | a ≠ b ≠ c | α = β = γ = 90° |
| jednoskośny | a ≠ b ≠ c ≠ a | α = γ = 90°; β ≠ 90° |
| trójskośny | a ≠ b ≠ c ≠ a | α ≠ β ≠ γ ≠ α α, β, γ ≠ 90° |
| heksagonalny | a = b ≠ c | α = β = 90°; γ = 120° |
| trygonalny (romboedryczny) |
a = b ≠ c (a = b = c) |
α = β = 90°; γ = 120° (α = β = γ ≠ 90°) |
Sieć Bravais’go[edytuj | edytuj kod]
Układ krystalograficzny opisuje się często za pomocą sieci Bravais’go. Jest to sposób wypełnienia przestrzeni przez wielokrotne powtarzanie operacji translacji komórki elementarnej. Sieci Bravais’go uzyskiwane są przez złożenie siedmiu układów krystalograficznych i czterech sposobów centrowania (P – prymitywne; C – centrowanie na podstawach; F – centrowanie na wszystkich ścianach; I – centrowanie przestrzenne). Jeżeli rozpatruje się układ trygonalny jako romboedryczną wersję układu heksagonalnego to jest on oznaczany przez literę R. Spośród teoretycznie możliwych 28 (7 · 4) sposobów występuje tylko 14[3]:
| Układ | Liczba możliwości | Możliwe sieci Bravais’go |
|---|---|---|
| Regularny | 3 | prymitywna (P), przestrzennie centrowana (I), ściennie centrowana (F) |
| Tetragonalny | 2 | prymitywna (P), przestrzennie centrowana (I) |
| Rombowy | 4 | prymitywna (P), przestrzennie centrowana (I), ściennie centrowana (F), centrowana na podstawach (C) |
| Jednoskośny | 2 | prymitywna (P), centrowana na podstawach (C) |
| Trójskośny | 1 | prymitywna (P) |
| Heksagonalny | 1 | prymitywna (P) |
| Trygonalny[a] | 1 | prymitywna (P) |
| Rodzina krystalograficzna[b][3] |
Układ krystalograficzny |
Typ komórki Bravais’go[3] |
Symbol Pearsona[3] |
Główne translacje[3] | Liczba węzłów[c][3] |
Geometria komórki elementarnej |
|---|---|---|---|---|---|---|
| trójskośny | 
| |||||
| jednoskośny | 
| |||||

| ||||||
| rombowy | 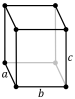
| |||||

| ||||||
| Parser nie mógł rozpoznać (SVG (MathML może zostać włączone przez wtyczkę w przeglądarce): Nieprawidłowa odpowiedź („Math extension cannot connect to Restbase.”) z serwera „http://localhost:6011/pl.wikipedia.org/v1/”:): {\displaystyle 2} | 
| |||||

| ||||||
| tetragonalny | 
| |||||

| ||||||
| heksagonalny | heksagonalny | 
| ||||
| trygonalny[d] | 
| |||||
| regularny | 
| |||||

| ||||||

| ||||||
Zobacz też[edytuj | edytuj kod]
Uwagi[edytuj | edytuj kod]
- ↑ W niektórych podziałach występuje jako odmiana romboedryczna układu heksagonalnego.
- ↑ Zgodnie z podziałem Tablic Międzynarodowych.
- ↑ Liczba węzłów przypadających na jedną komórkę elementarną.
- ↑ W niektórych podziałach występuje jako osobny układ trygonalny/romboedryczny.
Przypisy[edytuj | edytuj kod]
- ↑ a b Trzaska Durski Z., Trzaska Durska H.: Podstawy krystalografii. Warszawa: OW Politechniki Warszawskiej, 2003, s. 141–143. ISBN 83-7207-438-0.
- ↑ Krystalografia. Warszawa: Wydawnictwo Naukowe PWN, 2007. ISBN 978-83-01-14704-4.
- ↑ a b c d e f Trzaska Durski Z., Trzaska Durska H.: Podstawy krystalografii. Warszawa: OW Politechniki Warszawskiej, 2003, s. 55–57. ISBN 83-7207-438-0.




































