Hydrostatyka
Hydrostatyka (z gr. hydōr – „woda” + statikos – „powodujący stanie”) – dział mechaniki płynów zajmujący się badaniem cieczy w stanie spoczynku[1] oraz warunków pozostawania w spoczynku cieczy znajdującej się w polu sił masowych.
Siłami masowymi są siły, których wartość jest proporcjonalna do masy ciała, czyli siły grawitacyjne oraz sił bezwładności. Pomimo że istnieje odrębna dziedzina nauki zajmująca się jedynie statyką gazów (aerostatyka), ze względu na liczne pokrewieństwa (zarówno w samych zjawiskach, jak i ich opisach), często ciecze i gazy są rozpatrywane wspólnie (mechanika płynów).
Współczesność[edytuj | edytuj kod]
Współcześnie podstawowym zagadnieniem hydrostatyki jest określenie skalarnego pola ciśnienia w cieczy znajdującej się w spoczynku. Ciśnienie opisuje równanie:
gdzie:
- – wektorowe pole jednostkowych sił masowych (siła działająca na jednostkę masy cieczy),
- – gęstość cieczy,
- – ciśnienie,
- – dywergencja.
Zależność ta wynika z zastosowania praw dynamiki Newtona, które mogą być wyrażone dla płynu przez równania Naviera-Stokesa przy założeniu, że prędkość jest równa zero. Spełnione ono jest zarówno dla płynów nieściśliwych, czyli idealnych cieczy, jak i dla płynów ściśliwych, gdy pomija się ruch płynu wywołany ściśliwością; rzeczywistych cieczy i gazów.
Prawa strona równania jest różniczką, oznacza to że płyn pozostaje w spoczynku dla sił masowych będących różniczkowalnymi, takie pole sił jest polem potencjalnym. Ciśnienie oraz gęstość płynu w spoczynku w polu potencjalnym na powierzchni o jednakowym potencjale (ekwipotencjalnej) są jednakowe[2]. Jeśli ciało składa się z dwóch płynów o różnej gęstości to powierzchnia rozdziału jest powierzchnią ekwipotencjalną, płyn o większej gęstości zajmuje obszar o mniejszej energii[2].
Prawo Pascala[edytuj | edytuj kod]
Gdy nie występują siły masowe równanie upraszcza się do:
Oznacza to że, gdy w płynie nie występują siły masowe, to ciśnienie w płynie jest jednakowe we wszystkich punktach płynu. Prawidłowość tę po raz pierwszy sformułował Pascal, stąd jego nazwa prawo Pascala i tradycyjnie jest uważane za najważniejsze prawo hydrostatyki.
Ciecz w polu jednorodnym[edytuj | edytuj kod]
Gdy siła masowa jest jednakowa w całej objętości cieczy i skierowana wzdłuż osi to ciśnienie zależy tylko od tej współrzędnej, a równanie równowagi płynu można sprowadzić do postaci:
lub
gdzie:
- – siła jednostkowa w kierunku osi
- – zmiana położenia,
- – zmiana ciśnienia.
Gdy gęstość płynu nie zależy od ciśnienia, co jest w przybliżeniu spełnione dla wszystkich cieczy, a siła masowa jest przyspieszeniem ziemskim równanie opisujące ciśnienie w cieczy zapisuje się w postaci:
gdzie:
- – ciśnienie panujące w cieczy na głębokości
- – ciśnienie panujące na powierzchni cieczy,
- – głębokość, na której określane jest ciśnienie.
W gazach, w tym i w powietrzu, gęstość można obliczyć z równania Clapeyrona. Jest ona zależna od ciśnienia:
gdzie:
- – masa molowa gazu,
- – stała gazowa,
- – temperatura gazu.
Z powyższego wynika zależność ciśnienia gazu od wysokości:
Co prowadzi do równania na zależność gęstości gazu od wysokości
gdzie:
- – wysokość,
- – zwana skalą wysokości.
Równania powyższe zwane są formułą barometryczną służą do wyznaczania ciśnienia w powietrzu na różnych wysokościach.
Wstęp[edytuj | edytuj kod]
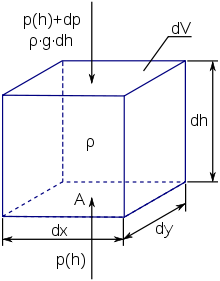
Kluczowym pojęciem w hydrostatyce jest ciśnienie. Ciśnienie jest stosunkiem siły przypadającej na powierzchnię jednostkową:
W celu otrzymania wyrażenia łączącego siłę z ciśnieniem dla objętości różniczkowej wychodzi się z równania różniczkowego opisującego zmianę ciśnienia w kierunku osi OZ:
Po zsumowaniu równań dla wszystkich kierunków równanie przyjmuje postać:
Jeżeli wartość dF podzielimy przez objętość różniczkową otrzymamy:
Co można zapisać:
Ciśnienie cieczy (w układach rzeczywistych) zależy jedynie od głębokości (ilości cieczy ponad punktem pomiaru). Jeżeli przyjmiemy, że g oraz są jednakowe dla każdego punktu w cieczy ( = idem i dg = idem) to zmiana ciśnienia w zależności od głębokości będzie miała charakter liniowy, co można wyrazić wzorem:
gdzie:
- – gęstość cieczy,
- – przyspieszenie ziemskie,
- – wysokość cieczy.
Jeżeli w dwóch pojemnikach (patrz rys. 2) znajduje się ciecz o tej samej wysokości i gęstości, to na dno obu pojemników wywierane jest takie samo ciśnienie. Dzieje się tak dlatego, że ciecz nad pochyłymi ściankami zbiornika b wywiera ciśnienie na te ścianki, a nie na dno zbiornika.

Jeżeli w pojemniku znajdują się ciecze o różnej gęstości (nie mieszające się) to ciśnienie na danej głębokości jest sumą ciśnień wywieranych przez ciecze położone wyżej (o niższej gęstości) i wyraża się wzorem:
gdzie:
- – gęstość -tej cieczy,
- – wysokość warstwy -tej cieczy,
- – przyspieszenie ziemskie.
Jeżeli ciecze w zbiorniku mieszają się (nie tworzą warstw) to gęstość można zastąpić średnią gęstością cieczy:
gdzie:
- – gęstość -tej cieczy.
- – ułamek objętościowy -tej cieczy.
Właściwości statyczne płynów[edytuj | edytuj kod]
Płyny w stanie spoczynku posiadają pewne właściwości, dzięki którym mogą być charakteryzowane. Należą do nich:
- gęstość
Stosunek masy do objętości:
- gęstość względna
Stosunek gęstości cieczy do gęstości wody. Ponieważ gęstość wody wynosi w przybliżeniu to gęstość względna cieczy wynosi w przybliżeniu wartość jednej tysięcznej gęstości tej cieczy. Gęstość względną wyraża się wzorem:
- ciężar właściwy
Ciężar przypadający na objętość jednostkową:
- objętość właściwa
Stosunek objętości cieczy do masy (odwrotność gęstości):
- współczynnik rozszerzalności cieplnej
Stosunek zmiany jednostki objętości płynu w wyniku zmiany temperatury o jednostkę temperatury
- współczynnik ściśliwości
Stosunek zmiany jednostki objętości płynu pod wpływem zmiany ciśnienia o jednostkę

- ciepło właściwe
Jest to energia potrzebna do podniesienia temperatury jednostki masy ciała o jednostkę temperatury:
Oznaczenia:
Prawa hydrostatyki[edytuj | edytuj kod]

Istnieją trzy podstawowe prawa, które odgrywają ogromną rolę w hydrostatyce:
Prawo Archimedesa[edytuj | edytuj kod]
Prawo Archimedesa brzmi: Na ciało zanurzone w płynie działa pionowa, skierowana ku górze siła wyporu. Wartość siły jest równa ciężarowi wypartej cieczy (gazu). Siła jest przyłożona w środku ciężkości wypartej cieczy (gazu).
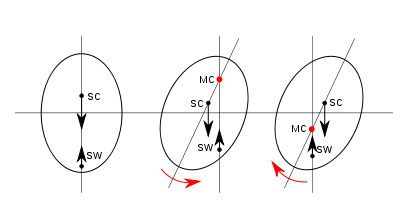
Prawo to pomaga też wyjaśnić zachowanie się ciał częściowo zanurzonych w wodzie (pływających). Ciało częściowo zanurzone w wodzie (rys. 3) ma środek ciężkości (SC) oraz środek wyporności (SW). Przy zmianie kąta pochylenia położenie środka wyporności ulega zmianie, a ciało może wrócić do pozycji początkowej (stabilne) lub odchylić się całkowicie (niestabilne). O tym czy ciało jest stabilne czy nie, decyduje położenie metacentrum (MC). Metacentrum jest punktem, w którym oś ciała przecina się z linią pionową przecinającą środek wyporności. Dla małych zmian kąta pochylenia jego położenie jest niezależne od kąta. Jeżeli metacentrum znajduje się powyżej środka ciężkości to ciało pod wpływem powstałego układu sił wróci do stanu początkowego (rys. 3b). Jeżeli natomiast metacentrum leży poniżej środka ciężkości ciało pochyli się całkowicie (rys. 3c). Odcinek od metacentrum do środka ciężkości nazywa się wysokością metacentryczną. Obliczenia takie stosuje się np. przy projektowaniu statków. Statki projektuje się tak, aby były one jak najbardziej stateczne i w razie przechylenia samoczynnie wracały do pozycji początkowej.
Prawo Eulera[edytuj | edytuj kod]
Sformułowane przez Eulera w 1755 roku mówi, że[3]:
Na płaskie ciało zanurzone w cieczy działa ciśnienie, którego wartość jest niezależna od orientacji tego ciała w przestrzeni.
W celu otrzymania matematycznej zależności opisującej to prawo rozpatrzmy różniczkową objętość płynu o podstawie trójkątnej i wysokości b (rys. 4). Płyn znajduje się w stanie równowagi (spoczynku). W stanie równowagi suma sił w poszczególnych kierunkach musi być równa zero:

Ponieważ:
Po podstawieniu otrzymujemy ostatecznie:
Prawo Pascala[edytuj | edytuj kod]
Prawo Pascala mówi, że jeżeli na ciecz lub gaz w zbiorniku zamkniętym wywierane jest ciśnienie zewnętrzne, to ciśnienie wewnątrz zbiornika jest wszędzie jednakowe i równe ciśnieniu zewnętrznemu.
Prawo to jest spełnione dla cieczy, na którą działają jedynie siły powierzchniowe. Oznacza to, że dotyczy cieczy, które nie znajdują się w polu sił grawitacyjnych. W warunkach rzeczywistych (gdy na ciecz działają dodatkowo siły grawitacji) cząsteczki z niższych warstw cieczy muszą „udźwignąć” cząsteczki znajdujące się nad nimi. Powoduje to różnice ciśnień między górną a dolną warstwą cieczy. Prawo często stosuje się w inżynierii (np. przy konstrukcji pras hydraulicznych, akumulatorów ciśnienia oraz tam).
Płaszczyzna zanurzona w cieczy[edytuj | edytuj kod]

Ciało (płaskie) zanurzone w cieczy podlega działaniu sił (rys. 6)[4][5]. Jeżeli pominie się siłę ciężkości tego ciała i założy, że działają na nie tylko siły powierzchniowe, to przy obliczeniach uwzględnia się jedynie siły pochodzące od cieczy. Ponieważ powierzchnia jest nachylona pod kątem to na każdy element powierzchni działa inne ciśnienie pochodzące od cieczy (ponieważ każdy element powierzchni leży na innej głębokości) natomiast ciśnienie atmosferyczne jest jednorodne dla całej powierzchni. Siłę wypadkową można zapisać jako sumę iloczynów wszystkich nieskończenie małych elementów powierzchni i ciśnień na nie padających:
Jeżeli rozpiszemy ciśnienie jako sumę ciśnienia atmosferycznego (stałego) i ciśnienia pochodzącego od cieczy to otrzymamy:
Jeżeli przyjmiemy to wyrażenie to można zapisać jako:
Ponieważ średnie (dla punktu C – środka ciężkości) równa się:
Stąd ostatecznie:
Obliczona siła wypadkowa przyłożona jest w punkcie P – środku ciśnienia. Jego współrzędne oznaczymy jako oraz Aby obliczyć te współrzędne dodajemy momenty sił względem środka ciężkości i uzyskujemy postać równania:
Po przekształceniu:
Jeżeli wprowadzimy
to otrzymamy:
Ponieważ
gdzie – moment bezwładności.
Przekształcając równanie możemy obliczyć odległość od środka ciężkości:
Analogicznie obliczenia przeprowadza się dla współrzędnej
Wartości momentów bezwładności dla najczęściej spotykanych figur płaskich podano w tabelach poniżej.
|
|
|
|
|
Ciecz w stanie bezwładności[edytuj | edytuj kod]

Jeżeli umieścimy ciecz w wirówce i poddamy działaniu sił to po pewnym czasie cała ciecz zostanie wprawiona w ruch i osiągnie stan bezwładności, zachowując się jak sztywne ciało. Ciecz znajdująca się w takim stanie jest przedmiotem badań hydrostatyki.
Aby opisać ciecz zachowującą się jak ciało sztywne, kręcące się wokół osi należy uwzględnić oprócz sił ciężkości, wynikających z przyspieszenia ziemskiego, również siły odśrodkowe, wynikające z przyspieszenia skierowanego do osi obrotu.
Zakładamy, że ciało obraca się ze stałą prędkością kątową Promień obrotu, który łączy oś obrotu z objętością różniczkową, którą badamy, oznaczamy jako
Przyspieszenie zgodnie z zasadami mechaniki (kinetyki) jest równe:
gdzie
Gradient ciśnienia równa się zmianie siły objętościowej:
Aby uzyskać wyrażenie na wartość ciśnienia całkujemy drugie równanie otrzymując:
gdzie to stała wyrażona jako funkcja '. Następnie różniczkujemy po
I przyrównując do równania wcześniej otrzymanego:
Całkujemy:
gdzie to stała całkowania. Z warunków początkowych (dla i ) otrzymujemy równanie na wartość ciśnienia:
Pomiar ciśnienia[edytuj | edytuj kod]



Pomiarów ciśnienia dokonuje się przy pomocy urządzeń zwanych ciśnieniomierzami. Ciśnieniomierze dzielimy na manometry (do pomiaru nadciśnienia) oraz wakuometry (do pomiaru podciśnienia). Często nazwy manometr używa się jako synonimu ciśnieniomierz. Manometry różnią się między sobą zasadą działania. Można dokonać ich ogólnego podziału manometrów na:
- grawitacyjne – wykorzystują siłę grawitacji do bezpośredniego pomiaru ciśnienia. Przykładem może być manometr w postaci U-rurki (patrz poniżej). Zamiast słupa cieczy jako przeciwwagi niekiedy wykorzystuje się obciążenie (dzwon). Zakres mierzonego ciśnienia dla manometrów U-rurkowych: od MPa do 0,1 MPa[6].
- sprężynowe – mierzą odkształcenie jakie następuje pod wpływem ciśnienia. Ciśnieniomierze tego typu przybierają rozmaite formy.
- rurki Bourdona (rys. 9) – manometry zbudowane z wygiętej (najczęściej pod kątem ok. 250°) rurki wypełnionej płynem. Pod wpływem przyłożonego ciśnienia rurka prostuje się. Wskazówka manometru przesuwa się proporcjonalnie do wygięcia rurki. Przy pomiarze wysokich ciśnień wykorzystuje się manometry wyposażone w kilka rurek (spiralę). Zakres pomiaru takich urządzeń wynosi: od 0,06 MPa do 400 MPa[6].
- membranowe – działają na podobnej zasadzie jak rurki Bourdona, jednak w tym przypadku elementem odkształcalnym jest membrana, której odkształcenie jest wprost proporcjonalne do przyłożonego ciśnienia. Istnieje możliwość sterowania wielkością siły aktywującej odkształcenie. Zakres stosowania: od 0,0016 MPa do 4 MPa[6].
- elektroniczne – mierzące takie właściwości jak opór elektryczny, indukcyjność, częstotliwość rezonansu, przetwarzające bezpośrednio wartość ciśnienia na sygnał elektryczny, stosowane w układach automatyki przemysłowej.
Klasyczny manometr ma postać U-rurki (rys. 8) wypełnionej cieczą (najczęściej wodą lub innym medium, np. czterochlorkiem węgla) oraz podziałką. Jeden koniec podłączony jest do zbiornika, w którym panuje ciśnienie, które jest mierzone, a drugi zazwyczaj jest otwarty (do atmosfery). Zasadę działania klasycznego manometru można wyjaśnić przy pomocy praw hydrostatyki. Suma ciśnień w lewej części U-rurki musi być równa sumie ciśnień w prawej części. Jeżeli obie części U-rurki są podłączone do atmosfery to poziomy cieczy po obu stronach są równe (rys. 8a). Jeżeli podłączymy jedną stronę U-rurki do zbiornika, w którym panuje nadciśnienie to ciecz przesunie się w lewą stronę (rys. 8b). Przesunięcie będzie proporcjonalne do nadciśnienia w zbiorniku. Dla przedstawionego układu równowagę można zapisać:
gdzie:
- – ciśnienie atmosferyczne,
- – różnica wysokości słupa cieczy,
- – gęstość cieczy,
- – ciśnienie w zbiorniku.
Obecnie w przemyśle, oprócz klasycznych ciśnieniomierzy, stosuje się bardziej złożone układy (mechaniczne lub elektroniczne) do pomiaru ciśnienia. Zaletą urządzeń elektronicznych jest uzyskanie informacji w postaci cyfrowej oraz możliwość bezpośredniej współpracy z komputerem. Zaletą klasycznych manometrów jest cena i niezawodność.
Zobacz też[edytuj | edytuj kod]
Przypisy[edytuj | edytuj kod]
- ↑ hydrostatyka, [w:] Encyklopedia PWN [dostęp 2022-11-28].
- ↑ a b Alicja Kordas: Mechanika płynów. Wrocław: Oficyna Wydawnicza Politechniki Wrocławskiej, 2001, s. 82. ISBN 83-7085-597-0.
- ↑ M. Serwiński, Zasady inżynierii chemicznej – operacje jednostkowe, Wydawnictwa Naukowo-Techniczne, Warszawa 1971.
- ↑ F.Kreith, Mechanical Engineering Handbook, CRC Press, 1999, ISBN 0-8493-9751-0.
- ↑ F.M.White, Fluid Mechanics, McGraw-Hill, 2003, ISBN 0-07-240217-2.
- ↑ a b c Manometry.








































![{\displaystyle \rho =\lim _{dV\to 0}{\frac {dm}{dV}}\left[\mathrm {\frac {kg}{m^{3}}} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8351099a40d593d8c5f0ee0bee75321940264246)
![{\displaystyle 1000[kg/m^{3}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4036b237bde5645d00a51fbadf52c7613d0b4c06)
![{\displaystyle s={\frac {\rho _{cieczy}}{\rho _{wody}}}[-]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bc2d1f310095be718f990deb08f926692488b7b)
![{\displaystyle \gamma =\lim _{dV\to 0}{\frac {dF}{dV}}\left[\mathrm {\frac {N}{m^{3}}} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e53e87d2a4c15f949e410298ca82b5c3793c3a8)
![{\displaystyle \upsilon =\lim _{dm\to 0}{\frac {dV}{dm}}\left[\mathrm {\frac {m^{3}}{kg}} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ec7e25b020039afaa5651bfed55aa46f7157dc1)
![{\displaystyle \beta =-{\frac {\partial V}{\partial t}}\cdot {\frac {1}{V}}\left[{\frac {1}{^{\circ }}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc52b0030360ed11fdd72868614294239bf92d15)
![{\displaystyle \alpha ={\frac {\partial V}{\partial p}}\cdot {\frac {1}{V}}\left[\mathrm {{\frac {1}{Pa}}={\frac {m\cdot s}{kg}}} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9baa5d250b5997ca97f89af5e03de0cb12ae7642)
![{\displaystyle c={\frac {t}{N}}\left({\frac {\partial S}{\partial t}}\right)\left[\mathrm {\frac {J}{kg\cdot K}} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fd80b0a82c628f3da9ad4f90300c08f4e1fdf3c)