Testy doświadczalne ogólnej teorii względności
Testy doświadczalne ogólnej teorii względności mają na celu dostarczenie obserwacyjnych dowodów na rzecz ogólnej teorii względności. Pierwsze trzy testy zaproponowane przez Alberta Einsteina w roku 1915 dotyczyły anomalnej precesji peryhelium Merkurego, odchylenia światła w polu grawitacyjnym oraz grawitacyjnego przesunięcia ku czerwieni. Precesja Merkurego była już znana, pierwsze obserwacje odchylenia światła zgodne z przewidywaniami teorii względności zostały przeprowadzone w 1919, przy czym bardziej dokładne pomiary przeprowadzano w następnych latach, astrofizyczne pomiary grawitacyjnego przesunięcia ku czerwieni przeprowadzono w roku 1925, jednak pomiary wystarczająco czułe do potwierdzenia teorii nie zostały wykonane do roku 1954. Program dokładniejszych testów rozpoczynający się w roku 1959 zweryfikował różne przewidywania teorii względności z większym stopniem dokładności w zakresie słabego pola grawitacyjnego, mocno ograniczając możliwe odchylenia względem przewidywań teorii.
W latach siedemdziesiątych zostały wykonane kolejne testy, poczynając od pomiaru relatywistycznej dylatacji czasu sygnału radarowego w pobliżu Słońca przeprowadzonego przez Irwina Shapiro. Począwszy od roku 1974, Hulse, Taylor i inni badali zachowanie pulsarów podwójnych o masach powodujących znacznie większe zakrzywienie czasoprzestrzeni niż to, które występuje w Układzie Słonecznym. Zarówno w granicy słabego pola grawitacyjnego (jak w Układzie Słonecznym) jak i w silniejszych polach występujących w układach pulsarów podwójnych przewidywania ogólnej teorii względności zostały lokalnie bardzo dobrze potwierdzone.
W lutym 2016 grupa badaczy z detektora LIGO doniosła o bezpośrednim wykryciu fal grawitacyjnych, pochodzących ze zderzenia czarnych dziur[1]. To odkrycie weryfikuje przewidywania ogólnej teorii względności w granicy bardzo silnego pola, nie znajdując jak do tej pory żadnych odchyleń od przewidywań teorii.
Klasyczne testy[edytuj | edytuj kod]
W roku 1916 Albert Einstein zaproponował[2][3] trzy testy ogólnej teorii względności, w następnych latach nazwane klasycznymi testami ogólnej teorii względności:
- precesje peryhelium orbity Merkurego
- ugięcie światła w polu grawitacyjnym Słońca
- grawitacyjne przesunięcie ku czerwieni
W liście do London Times z 28 listopada 1919 Einstein opisał teorie względności i podziękował brytyjskim naukowcom za zrozumienie i przetestowanie jego pracy. Wspomniał również o powyższych trzech klasycznych testach, dodając:[4]
- „Główna atrakcyjność tej teorii polega na logicznej zupełności. Jeżeli jeden z wyciągniętych z niej wniosków okazałby się błędny, musiałaby zostać porzucona, zmodyfikowanie jej bez zniszczenia całej struktury wydaje się niemożliwe”.
Precesja peryhelium Merkurego[edytuj | edytuj kod]

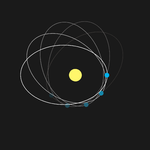
Według fizyki newtonowskiej układ dwóch ciał składający się z obiektu okrążającego sferycznie symetryczną masę zachowuje się w taki sposób, że ruch ciała próbnego wyznacza elipsę ze środkiem masy znajdującym się w jednym z jej ognisk. Punkt na orbicie, w którym poruszające się ciało znajduje się najbliżej źródła pola (nazywany apsydą lub w astronomii peryhelium, ze względu na fakt, że Słońce jest głównym źródłem pola grawitacyjnego w Układzie Słonecznym) pozostaje nieruchomy. Jednak w Układzie Słonecznym istnieje wiele innych czynników powodujących ruch peryheliów planet. Głównym czynnikiem jest obecność innych planet, których oddziaływanie wywołuje perturbacje. Innym, choć dużo słabszym czynnikiem, jest spłaszczenie Słońca.
Ruch Merkurego nie jest zgodny z przewidywaniami, które można wyprowadzić z grawitacji newtonowskiej. Anomalia prędkości precesji peryhelium została po raz pierwszy zaobserwowana w roku 1859 przez Le Verriera. Na podstawie obserwacji ruchu Merkurego prowadzonych od 1697 do 1848 roku Le Verrier ustalił, że rzeczywiste tempo precesji odbiega od przewidywań teorii Newtona o 38″ na wiek zwrotnikowy (w roku 1882 dokładniejsze oszacowanie 43″ zostało podane przez Simona Newcomba)[5]. Zaproponowano szereg doraźnych wyjaśnień tych efektów, jednak powodowały one kolejne większe problemy.
Brakująca wartość w prędkości precesji została ostatecznie wyjaśniona na bazie ogólnej teorii względności. Einstein pokazał, że ogólna teoria względności daje przewidywania dokładnie zgodne z obserwowaną wartością przesunięcia peryhelium[2]. Wyjaśnienie prędkości precesji Merkurego odegrało bardzo ważną rolę w procesie akceptacji ogólnej teorii względności. W ostatnich latach Friedman i Steiner[6] wyjaśnili obserwowaną wielkość przesunięcia peryhelium bez pełnej ogólnej teorii względności, jedynie w ramach modelu relatywistycznej dynamiki newtonowskiej (RND).
Wcześniejsze pomiary ruchu planet były wykonywane przy pomocy tradycyjnych teleskopów, natomiast współcześnie przeprowadzono bardziej dokładne pomiary wykorzystując metody radarowe. Całkowita zmierzona precesja wynosi 574,10″±0,65 na wiek[7] względem Międzynarodowego Niebieskiego Układu Odniesienia (ICRF). Taka wartość precesji jest uważana za wypadkowy efekt następujących przyczyn:
| Wielkość[8] | Przyczyna |
|---|---|
| 532,3035 | Oddziaływanie grawitacyjne innych ciał Układu Słonecznego |
| 0,0286 | Spłaszczenie Słońca |
| 42,9799 | Zakrzywienie czasoprzestrzeni (zakładając czasoprzestrzeń Schwarzschilda) |
| −0,0020 | Efekt Lense-Thirringa |
| 575,31 | Całkowita oczekiwana precesja |
| 574,10±0,65[7] | Obserwowana precesja |
Zatem efekt może być całkowicie wyjaśniony na gruncie ogólnej teorii względności. Najnowsze obliczenia bazujące na bardziej dokładnych pomiarach nie zmieniły zasadniczo sytuacji.
W ogólnej teorii względności przesuniecie peryhelium wyrażone w radianach na obrót jest w przybliżeniu dane wzorem:[9]
gdzie L jest półosią wielką, T jest okresem orbitalnym, c jest prędkością światła i e jest mimośrodem orbity (zobacz: problem dwóch ciał w ogólnej teorii względności).
Co więcej powyższy wzór jest dokładnym wyrażeniem na prędkość precesji peryhelium w ramach relatywistycznej dynamiki newtonowskiej[10].
Ruch innych planet również wykazuje precesje peryhelium orbity, jednak z uwagi na odległość od Słońca w jakiej się znajdują, jak również ich okresy orbitalne, precesja jest mniejsza i została zaobserwowana na długo po odkryciu precesji peryhelium Merkurego. Na przykład precesja peryhelium Wenus i Ziemi, zgodnie z ogólną teorią względności, wynosi odpowiednio 8,62″ i 3,84″ (sekund łukowych) na wiek. Obie wartości zostały zmierzone z wynikiem zgodnym z teorią[11]. Wykonano również pomiary ruchu perycentrum w układzie pulsarów podwójnych PSR 1913+16 z wartością 4.2º na rok[12]. Jest to wynik spójny z przewidywaniami ogólnej teorii względności[13]. Istnieje także możliwość wykonania pomiarów dla układów gwiazd podwójnych, które nie zawierają ultra gęstych gwiazd (takich jak pulsary), jednakże w przypadku takich obserwacji pozostaje problem dokładnego modelowania klasycznych zjawisk – na przykład prawidłowa interpretacja pomiaru wymaga dokładnej znajomości momentów pędu gwiazd względem ich płaszczymy orbitalnej. Dla kilku układów gwiazd np. DI Herculis[14] takie pomiary zostały wykonane w ramach testów ogólnej teorii względności.
Ugięcie światła w polu grawitacyjnym Słońca[edytuj | edytuj kod]

Henry Cavendish w roku 1784 (w nieopublikowanej pracy) i Johann Georg von Soldner w roku 1801 (w pracy opublikowanej w 1804) zwrócili uwagę, że z newtonowskiej teorii grawitacji wynika ze światło zakrzywi się w polu grawitacyjnym[15][16]. W 1911 Einstein powtórzył obliczenia Solder'a z takim samym wynikiem bazując jedynie na zasadzie równoważności. Natomiast w 1915 w trakcie pracy nad ogólną teorią względności Einstein zauważył, że jego wynik (a tym samym również Solder'a) stanowi zaledwie połowę poprawnej wartości. Einstein jako pierwszy wykonał prawidłowe obliczenie w oparciu o ogólną teorię względności[17].
Pierwsze testy ugięcia światła w polu grawitacyjnym polegały na obserwacji zmian położenia gwiazd na sferze niebieskiej w pobliżu Słońca. Obserwacje zostały wykonane przez Arthura Eddingtona i jego współpracowników podczas całkowitego zaćmienia Słońca 29 maja 1919[18], które pozwoliło zaobserwować położenie gwiazd w pobliżu Słońca (konstelacja Byka)[18]. Obserwacje zostały wykonane jednocześnie w miastach Sobral, Ceará, Brazil i w Sao Tomé i Príncipe na zachodnim wybrzeżu Afryki[19]. Ich pozytywny rezultat został uznany za spektakularny a informacja o nim pojawiła się na pierwszych stronach większości ówczesnych gazet. Wskutek tego Einstein wraz ze swoją teorią stał się sławny na skalę światową. Kiedy został zapytany przez swojego asystenta jak zareagowałby na wieść, że obserwacje Eddigntona i Dysona z 1919 nie potwierdziły jego teorii, Einstein zażartował: "Byłoby mi naprawdę przykro drogi panie. Teoria byłaby mimo wszystko prawdziwa."[20]
Jednakże dokładność wczesnych pomiarów była niewielka. Niektórzy twierdzili[21], że obserwacje Eddinghtona mogły być stronnicze i obciążone błędami systematycznymi. Natomiast współczesne analizy danych Eddingtona[22] sugerują, że pomiary były dokładne[23][24]. Obserwacje zostały powtórzone przez badaczy z Lick Obserwavtory podczas zaćmienia w 1922 z rezultatem zgodnym z tym który otrzymano w 1919[24]. W następnych latach tego rodzaju obserwacje były powtarzane kilkukrotnie, na przykład w 1953 przez astronomów z Yerkes Obserwavtory[25] i w 1973 przez grupę z Univesity of Texas[26]. Tego rodzaju pomiary były obciążone znaczną niepewnością przez blisko 50 lat, do czasu kiedy zaczęto przeprowadzać pomiary w częstotliwościach radiowych[27]. Pierścień Einsteina jest przykładem ugięcia światła pochodzącego z odległych galaktyk w polu grawitacyjnym bliższych obiektów[28].
Grawitacyjne przesunięcie ku czerwieni[edytuj | edytuj kod]

Einstein przewidział grawitacyjne przesuniecie ku czerwieni w roku 1907 jako konsekwencje zasady równoważności. Przewidywano, że tego rodzaju efekt mógłby zostać zaobserwowany w liniach spektralnych widma białego karla o bardzo silnym polu grawitacyjnym. Pierwsze próby pomiaru grawitacyjnego przesunięcia ku czerwieni zostały przeprowadzone przez Waltera Sydneya Adamsa w roku 1925 i dotyczyły linii spektralnych Syriusza B. Aczkolwiek te pomiary zostały skrytykowane z uwagi na zanieczyszczenie pomiaru światłem pochodzącym z sąsiedniej (znacznie jaśniejszej) gwiazdy, Syriusza[29][30]. Pierwsze dokładne pomiary grawitacyjnego przesunięcia ku czerwieni w liniach spektralnych białego karła (40 Eridani B) zostały przeprowadzone przez Poppera w roku 1954 z wynikiem 21 km/s[30].
Przesunięcie ku czerwieni w widmie Syriusza B zostało ostatecznie zmierzone przez Greensteina w 1971 z wynikiem 89±19 km/s, następnie dokładniejsze pomiary z użyciem teleskopu Hubblea dały wynik 80,4±4,8 km/s.
Testy doświadczalne szczególnej teorii względności[edytuj | edytuj kod]
Ogólna teoria względności obejmuje szczególną teorie względności, a zatem eksperymenty weryfikujące przewidywania szczególnej teorii względności weryfikują także przewidywania ogólnej teorii względności. Jak wynika z zasady równoważności, symetria Lorentza jest lokalnie zachowana w nieobracających się, swobodnie spadających układach odniesienia. Informacje na temat eksperymentów weryfikujących symetrie Lorentza w warunkach, w których efekty grawitacyjne mogą zostać zaniedbane zostały opisane w artykule testy szczególnej teorii względności.
Współczesne testy[edytuj | edytuj kod]
Epoka współczesnych testów rozpoczęła się w znacznej mierze za sprawą Dickego i Schiffa, którzy zaprojektowali program testów ogólnej teorii względności[31][32][33]. Położyli nacisk nie tylko na klasyczne testy opisane powyżej, ale również na eksperymenty zerowe, testujące efekty, które w zasadzie mogłyby wystąpić w teorii grawitacji, ale nie występują w ogólnej teorii względności. Innymi ważnymi czynnikami było pojawienie się alternatywnych teorii grawitacji (w szczególności teorii skalarno-tensorowych takich jak teoria Bransa-Dickego[34]), parametrycznego systemu postnewtonowskiego, który opisuje ilościowo możliwe odchylenia od przewidywań ogólnej teorii względności oraz frameworku dla zasady równoważności.
Nowe odkrycia związane z eksploracją przestrzeni kosmicznej, elektroniką i fizyką materii skondensowanej pozwoliły na przeprowadzenie kolejnych precyzyjnych pomiarów takich jak eksperyment Pounda-Rebki, a także doświadczenia wykorzystujące interferometrie laserową lub transksiężycową transmisje laserową.
Parametryczny system postnewtonowski[edytuj | edytuj kod]
Analiza wczesnych testów ogólnej teorii względności była utrudniona z uwagi na brak jakichkolwiek konkurencyjnych teorii. Nie było wiadomo, jaki rodzaj testu mógłby odróżnić ogólną teorie względności od potencjalnych teorii alternatywnych. Ogólna teoria względności była jedyną znaną relatywistyczną teorią grawitacji, zgodną ze szczególną teorią względności i obserwacjami. Co więcej, uważa się, że OTW jest bardzo prostą i elegancką teorią. Sytuacja uległa zmianie wraz z pojawieniem się teorii Bransa-Dickego w 1960 roku. Jest to teoria prawdopodobnie prostsza, nie zawiera żadnych stałych wymiarowych, w przeciwieństwie do OTW spełnia zasadę Macha oraz hipotezę wielkich liczb Diraca (dwie filozoficzne idee, które miały zasadniczy wpływ na rozwój ogólnej teorii względności). Ostatecznie, doprowadziło to do stworzenia parametrycznego systemu postnewtonowskiego (rozwijany najpierw przez Nordtvedta, następnie przez Willa), który w ramach zbioru dziesięciu parametrów opisuje wszystkie możliwe odstępstwa od newtonowskiego prawa powszechnego ciążenia do pierwszego przybliżenia prędkości poruszających się obiektów. To pozwala na usystematyzowanie analiz odchyleń od przewidywań ogólnej teorii względności dla wolno poruszających się obiektów w słabych polach grawitacyjnych. Włożono wiele wysiłku w celu doświadczalnej weryfikacji możliwych naruszeń parametrów tego formalizmu i obecnie są one ściśle ograniczone.
Eksperymenty testujące zjawisko soczewkowania grawitacyjnego i opóźnienia światła weryfikują naruszenia tego samego parametru tzw. parametru Eddingtona (γ), który jest bezpośrednią parametryzacją stopnia ugięcia światła w polu grawitacyjnym. Jest on równy jedności (γ = 1) w ogólnej teorii względności i przyjmuje różne wartości w innych teoriach grawitacji (takich jak teoria Bransa-Dickego). Możliwe naruszenia parametru Eddingtona są jak dotąd najściślej ograniczone. Natomiast dokładne obserwacje precesji peryhelium Merkurego, jak również doświadczenia testujące silną zasadę równoważności pozwoliły na dobre ograniczenie naruszeń innych parametrów.
Jednym z planowanych celów misji BepiColombo jest weryfikacja ogólnej teorii względności poprzez precyzyjny pomiar parametrów gamma i beta parametrycznego systemu postnewtonowskiego[35].
Soczewkowanie grawitacyjne[edytuj | edytuj kod]
Jednym z najważniejszych testów ogólnej teorii względności jest soczewkowanie grawitacyjne. Tego typu zjawiska zostały zaobserwowane dla światła pochodzącego z odległych obiektów kosmicznych, jednak wszystkie czynniki wpływające na te pomiary nie mogą zostać niezależnie zweryfikowane i nie jest jasne w jaki sposób takie obserwacje ograniczają możliwe odstępstwa od przewidywań ogólnej teorii względności. Najbardziej precyzyjne testy są analogiczne do obserwacji Eddingtona z roku 1919, tzn. polegają na pomiarze ugięcia promieniowania pochodzącego z odległego źródła w polu grawitacyjnym Słońca. Obiektami, które najlepiej nadają się do wykonywania precyzyjnych analiz, są odlegle źródła silnego promieniowania radiowego, takie jak niektóre kwazary. Kierunkowa rozdzielczość każdego teleskopu jest w zasadzie ograniczona z uwagi na dyfrakcje, tego typu praktyczne ograniczenia dotyczą również radioteleskopów. Jednakże ważnym usprawnieniem, które pozwoliło na wysoką poprawę rozdzielczości pozycyjnej (z wielkości rzędu milisekund do mikrosekund kątowych), było zastosowanie interferometrii wielkobazowej (VLBI) polegającej na wykorzystaniu pomiarów z kilku radioteleskopów rozmieszczonych na kuli ziemskiej w dużej odległości od siebie. Ostatnie pomiary wykonane przez te teleskopy pozwoliły na pomiar ugięcia fal radiowych w polu grawitacyjnym Słońca z bardzo wysoką dokładnością, ograniczając możliwe naruszenie ugięcia przewidywanego w ramach ogólnej teorii względności do poziomu 0,03%[36]. Przy takim poziomie dokładności wszelkie źródła błędów systematycznych muszą być starannie rozważone w celu precyzyjnego ustalenia rzeczywistego położenia teleskopów. Należy wziąć pod uwagę takie efekty jak nutacja i rotacja Ziemi, refrakcja atmosferyczna, przesunięcia tektoniczne i efekty pływowe. Innym ważnym źródłem błędów jest wpływ korony słonecznej na propagacje sygnałów radiowych. Gaz zjonizowanych cząstek ponad powierzchnią Słońca – jak każdy ośrodek – posiada pewien współczynnik refrakcji, co również powoduje zakrzywienie toru fal elektromagnetycznych. Na szczęście ugięcie spowodowane refrakcją zależy od długości fali, podczas gdy relatywistyczne ugięcie nie wykazuje takiej zależności. Zatem dokładna analiza, bazująca na pomiarach dla różnych długości fali, pozwala wyeliminować to źródło błędu.
Obraz całego nieba jest lekko zniekształcony z powodu grawitacyjnego ugięcia światła w polu grawitacyjnym Słońca. Tego rodzaju efekt został zaobserwowany przez satelitę Europejskiej Agencji Kosmicznej Hippatracos, która wykonała pomiar położenia 105 gwiazd. Podczas całej misji zmierzono około 3,5 × 106 pozycji względnych, każda typowo z dokładnością 3 milisekund kątowych (dokładność dla wielkości gwiazdowych w przedziale 8-9). Ponieważ odchylenie grawitacyjne prostopadłe do kierunku Ziemia-Słońce wynosi już 4,07 milisekund kątowych, uwzględnienie poprawki wynikającej z grawitacyjnego ugięcia światła jest konieczne dla praktycznie wszystkich gwiazd.
Rozpoczęta w roku 2013 misja sondy kosmicznej Gaia ma na celu wykonie spisu miliarda gwiazd Drogi Mlecznej, a także zmierzenie ich pozycji z dokładnością 24 mikrosekund kątowych. Tym samym dostarczy to nowych dowodów zgodności grawitacyjnego ugięcia światła w polu grawitacyjnym Słońca z przewidywaniami ogólnej teorii względności[37].
Opóźnienie sygnału świetlnego[edytuj | edytuj kod]
Irwin I. Shapiro zaproponował inny test, spoza grupy klasycznych testów, który mógłby zweryfikować ogólną teorię względności w Układzie Słonecznym. Jest on czasami nazywany czwartym „klasycznym” testem ogólnej teorii względności. Test polega na pomiarze opóźnienia sygnału radarowego (opóźnienie Shapiro) na drodze od źródła do obiektu odbijającego (np. innej planety) i z powrotem[38]. Opóźnienie wynikające ze zwykłego zakrzywienia toru w pobliżu Słońca jest zbyt małe aby mogło zostać zmierzone (różnica oczekiwanego czasu w płaskiej i zakrzywionej czasoprzestrzeni spowodowana różną długością toru), jednak na opóźnienie sygnału wpływa również dylatacja czasu w potencjale grawitacyjnym Słońca. Wykonane pomiary dla sygnału odbijającego się od Merkurego i Wenus tuż przed i po zaćmieniu zgadzają się z ogólną teorią względności na poziomie 5%[39]. Podobne pomiary wykonane w ramach misji Cassini-Huygens dały wynik zgodny z ogólną teorią względności na poziomie 0,002% (według B. Berotttiego)[40]. Jednakże szczegółowe analizy[41][42] ujawniły, że zmierzona wartość parametru gamma (PPN) jest związana z pewnymi zjawiskami grawitomagnetycznymi wywoływanymi ruchem orbitalnym Słońca wokół barycentrum Układu Słonecznego. Były one implicite postulowane przez B. Berottti jako mające czysto ogólno relatywistyczne pochodzenie, ale ich teoretyczna wartość nigdy nie została zweryfikowana eksperymentalnie, co powoduje, że rzeczywista niepewność pomiaru parametru gamma jest większa (o czynnik rzędu 10) niż 0,002% jak twierdzi B. Berottti na łamach Nature.
Zastosowanie interferometrii wielkobazowej pozwoliło na zmierzenie zależnych od prędkości (grawitomagnetycznych) poprawek do opóźnienia Shapiro w polu magnetycznym Jowisza[43][44] i Saturna[45].
Przypisy[edytuj | edytuj kod]
- ↑ Davide Castelvecchi, Witze Witze. Einstein's gravitational waves found at last. „Nature News”, February 11, 2016. DOI: 10.1038/nature.2016.19361. [dostęp 2016-02-11].
- ↑ a b Albert Einstein. The Foundation of the General Theory of Relativity. „Annalen der Physik”. 49 (7), s. 769–822, 1916. DOI: 10.1002/andp.19163540702. Bibcode: 1916AnP...354..769E. [dostęp 2006-09-03].
- ↑ Albert Einstein. The Foundation of the General Theory of Relativity. „Annalen der Physik”. 49 (7), s. 769–822, 1916. DOI: 10.1002/andp.19163540702. Bibcode: 1916AnP...354..769E.
- ↑ Albert (1919) Einstein, What Is The Theory Of Relativity?, German History in Documents and Images [dostęp 2013-06-07].
- ↑ U. Le Verrier (1859), (in French),"Lettre de M. Le Verrier à M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète", Comptes rendus hebdomadaires des séances de l'Académie des sciences (Paris), vol. 49 (1859), pp.379–383.
- ↑ Y. Friedman, J. M. Steiner. Predicting Mercury's Precession using Simple Relativistic Newtonian Dynamics. „Europhysics Letters (EPL)”. 113, s. 39001, 2016. DOI: 10.1209/0295-5075/113/39001. arXiv:1603.02560. Bibcode: 2016EL....11339001F.
- ↑ a b G. M. Clemence. The Relativity Effect in Planetary Motions. „Reviews of Modern Physics”. 19 (4), s. 361–364, 1947. DOI: 10.1103/RevModPhys.19.361. Bibcode: 1947RvMP...19..361C.
- ↑ Ryan S. Park. Precession of Mercury’s Perihelion from Ranging to the MESSENGER Spacecraft. „The Astronomical Journal”. 153 (3), s. 121, 2017. DOI: 10.3847/1538-3881/aa5be2.
- ↑ Adrian-Horia Dediu, Luis Magdalena, Carlos Martín-Vide: Theory and Practice of Natural Computing: Fourth International Conference, TPNC 2015, Mieres, Spain, December 15-16, 2015. Proceedings. Wyd. illustrated. Springer, 2015, s. 141. ISBN 978-3-319-26841-5. Extract of page 141
- ↑ Y. Friedman, S. Livshitz, J. M. Steiner. Predicting the relativistic periastron advance of a binary star without curving spacetime. „Europhysics Letters (EPL)”. 116, s. 59001, 2016. DOI: 10.1209/0295-5075/116/59001. arXiv:1705.05705. Bibcode: 2016EL....11659001F.
- ↑ Abhijit Biswas, Krishnan R. S. Mani. Relativistic perihelion precession of orbits of Venus and the Earth. „Central European Journal of Physics”. 6 (3), s. 754–758, 2008. DOI: 10.2478/s11534-008-0081-6. Bibcode: 2008CEJPh...6..754B.
- ↑ Richard Alfred Matzner: Dictionary of geophysics, astrophysics, and astronomy. CRC Press, 2001, s. 356. ISBN 0-8493-2891-8.
- ↑ Weisberg, J.M.; Taylor, J.H. (July 2005). "The Relativistic Binary Pulsar B1913+16: Thirty Years of Observations and Analysis".
- ↑ Naeye, Robert, "Stellar Mystery Solved, Einstein Safe", Sky and Telescope, September 16, 2009. See also MIT Press Release, September 17, 2009. Accessed 8 June 2017.
- ↑ Soldner, J.G.V.. On the deflection of a light ray from its rectilinear motion, by the attraction of a celestial body at which it nearly passes by. „Berliner Astronomisches Jahrbuch”, s. 161–172, 1804.
- ↑ Domingos S.L. Soares, Newtonian gravitational deflection of light revisited, „arXiv:General Physics (physics.gen-ph)”, 2009, arXiv:physics/0508030.
- ↑ Will, C.M.. The Confrontation between General Relativity and Experiment. „Living Rev. Relativ.”. 17, s. 4, December 2014. DOI: 10.12942/lrr-2014-4. arXiv:gr-qc/0510072. Bibcode: 2006LRR.....9....3W. (ArXiv version here: arxiv.org/abs/1403.7377.)
- ↑ a b F. W. Dyson, Eddington, A. S., Davidson C.. A determination of the deflection of light by the Sun's gravitational field, from observations made at the total eclipse of 29 May 1919. „Philosophical Transactions of the Royal Society”. 220A, s. 291–333, 1920. DOI: 10.1098/rsta.1920.0009. Bibcode: 1920RSPTA.220..291D.
- ↑ Matthew Stanley. 'An Expedition to Heal the Wounds of War': The 1919 Eclipse and Eddington as Quaker Adventurer. „Isis”. 94 (1), s. 57–89, 2003. DOI: 10.1086/376099. PMID: 12725104.
- ↑ Rosenthal-Schneider, Ilse: Reality and Scientific Truth. Detroit: Wayne State University Press, 1980. p 74. See also Calaprice, Alice: The New Quotable Einstein. Princeton: Princeton University Press, 2005. p 227.
- ↑ Harry Collins and Trevor Pinch, The Golem, ISBN 0-521-47736-0
- ↑ Daniel Kennefick. Not Only Because of Theory: Dyson, Eddington and the Competing Myths of the 1919 Eclipse Expedition. „Studies in History and Philosophy of Science Part A”. 44, s. 89–101, 2007. DOI: 10.1016/j.shpsa.2012.07.010. arXiv:0709.0685.
- ↑ Philip Ball. Arthur Eddington was innocent!. „News@nature”, 2007. DOI: 10.1038/news070903-20.
- ↑ a b D. Kennefick, "Testing relativity from the 1919 eclipse- a question of bias", Physics Today, March 2009, pp. 37–42.
- ↑ van Biesbroeck, G.: The relativity shift at the 1952 February 25 eclipse of the Sun., Astronomical Journal, vol. 58, page 87, 1953.
- ↑ Texas Mauritanian Eclipse Team: Gravitational deflection of-light: solar eclipse of 30 June 1973 I. Description of procedures and final results., Astronomical Journal, vol. 81, page 452, 1976.
- ↑ Titov, O.; Girdiuk, A. (2015). Z. Malkin & N. Capitaine, ed. The deflection of light induced by the Sun's gravitational field and measured with geodetic VLBI. Proceedings of the Journées 2014 "Systèmes de référence spatio-temporels": Recent developments and prospects in ground-based and space astrometry.
- ↑ Nadia Drake: Einstein's 'Impossible' Experiment Finally Performed. 7 June 2017. [dostęp 2017-06-09].
- ↑ N. S. Hetherington. Sirius B and the gravitational redshift – an historical review. „Royal Astronomical Society, Quarterly Journal”. 21, s. 246-252, Sept. 1980. Bibcode: 1980QJRAS..21..246H.
- ↑ a b J. B. Holberg. Sirius B and the Measurement of the Gravitational Redshift. „Journal for the History of Astronomy”. 41 (1), s. 41-64, 2010. Bibcode: 2010JHA....41...41H.
- ↑ R. H. Dicke. New Research on Old Gravitation: Are the observed physical constants independent of the position, epoch, and velocity of the laboratory?. „Science”. 129 (3349), s. 621–624, March 6, 1959. DOI: 10.1126/science.129.3349.621. PMID: 17735811. Bibcode: 1959Sci...129..621D.
- ↑ Dicke, R. H. (1962). "Mach's Principle and Equivalence". Evidence for gravitational theories: proceedings of course 20 of the International School of Physics "Enrico Fermi" ed C. Møller.
- ↑ L. I. Schiff. On Experimental Tests of the General Theory of Relativity. „American Journal of Physics”. 28 (4), s. 340–343, April 1, 1960. DOI: 10.1119/1.1935800. Bibcode: 1960AmJPh..28..340S.
- ↑ C. H. Brans, Dicke, R. H.. Mach's Principle and a Relativistic Theory of Gravitation. „Physical Review”. 124 (3), s. 925–935, November 1, 1961. DOI: 10.1103/PhysRev.124.925. Bibcode: 1961PhRv..124..925B.
- ↑ Fact Sheet.
- ↑ E.B. Fomalont, Kopeikin S.M., Lanyi, G., Benson, J.. Progress in Measurements of the Gravitational Bending of Radio Waves Using the VLBA. „Astrophysical Journal”. 699 (2), s. 1395–1402, July 2009. DOI: 10.1088/0004-637X/699/2/1395. arXiv:0904.3992. Bibcode: 2009ApJ...699.1395F.
- ↑ esa: Gaia overview.
- ↑ I. I. Shapiro. Fourth test of general relativity. „Physical Review Letters”. 13 (26), s. 789–791, December 28, 1964. DOI: 10.1103/PhysRevLett.13.789. Bibcode: 1964PhRvL..13..789S.
- ↑ I.I. Shapiro i inni, Fourth Test of General Relativity: New Radar Result, „Physical Review Letters”, 26 (18), 1971, s. 1132–1135, DOI: 10.1103/PhysRevLett.26.1132, Bibcode: 1971PhRvL..26.1132S.
- ↑ Bertotti B., Iess L., Tortora P.. A test of general relativity using radio links with the Cassini spacecraft. „Nature”. 425 (6956), s. 374–376, 2003. DOI: 10.1038/nature01997. PMID: 14508481. Bibcode: 2003Natur.425..374B.
- ↑ Kopeikin S.~M., Polnarev A.~G., Schaefer G., Vlasov I.Yu.. Gravimagnetic effect of the barycentric motion of the Sun and determination of the post-Newtonian parameter γ in the Cassini experiment. „Physics Letters A”. 367 (4-5), s. 276–280, 2007. DOI: 10.1016/j.physleta.2007.03.036. arXiv:gr-qc/0604060. Bibcode: 2007PhLA..367..276K.
- ↑ Kopeikin S.~M.. Post-Newtonian limitations on measurement of the PPN parameters caused by motion of gravitating bodies. „Monthly Notices of the Royal Astronomical Society”. 399 (3), s. 1539-1552, 2009. DOI: 10.1111/j.1365-2966.2009.15387.x. arXiv:0809.3433. Bibcode: 2009MNRAS.399.1539K.
- ↑ E.B. Fomalont, Kopeikin S.M.. The Measurement of the Light Deflection from Jupiter: Experimental Results. „Astrophysical Journal”. 598 (1), s. 704–711, November 2003. DOI: 10.1086/378785. arXiv:astro-ph/0302294. Bibcode: 2003ApJ...598..704F.
- ↑ S.M. Kopeikin, Fomalont E.B.. Gravimagnetism, causality, and aberration of gravity in the gravitational light-ray deflection experiments. „General Relativity and Gravitation”. 39 (10), s. 1583–1624, October 2007. DOI: 10.1007/s10714-007-0483-6. arXiv:gr-qc/0510077. Bibcode: 2007GReGr..39.1583K.
- ↑ E.B. Fomalont, Kopeikin, S. M., Jones, D., Honma, M. i inni. Recent VLBA/VERA/IVS tests of general relativity. „Proceedings of the International Astronomical Union, IAU Symposium”. 261 (S261), s. 291–295, January 2010. DOI: 10.1017/S1743921309990536. arXiv:0912.3421. Bibcode: 2010IAUS..261..291F.



