Szczególna teoria względności

Szczególna teoria względności (STW) – teoria fizyczna stworzona przez Alberta Einsteina w 1905 roku[1][a]. Zmieniła ona sposób pojmowania czasu, przestrzeni i ruchu opisanych wcześniej w newtonowskiej mechanice, nazwanej potem nierelatywistyczną. Jednocześnie – zgodnie z zasadą korespondencji – mechanika Newtona pozostaje szczególnym przypadkiem tej Einsteina, a STW używa się głównie do opisu dużych prędkości, np. w fizyce cząstek elementarnych. Teoria Einsteina pozwoliła usunąć trudności interpretacyjne i sprzeczności pojawiające się na styku mechaniki, optyki i elektromagnetyzmu opracowanego przez Maxwella.
Najpóźniej od lat 30. XX w. STW jest teorią powszechnie zaakceptowaną i silnie potwierdzoną eksperymentalnie[2]. Wyjaśniła wiele wcześniejszych doświadczeń, jak aberracja światła, eksperyment Fizeau i doświadczenie Michelsona-Morleya. Została też potwierdzona przez badania późniejsze, jak doświadczenie Kennedy’ego-Thorndike’a, doświadczenie Ivesa-Stillwella i inne. Przewidywane przez nią efekty, jak np. dylatacja czasu, są wykorzystywane m.in. w technologii GPS. STW opiera się m.in. na postulacie, że prędkość światła w próżni jest niezmienna. Jest to fakt poświadczony z precyzją tak dużą, że w 1983 roku Generalna Konferencja Miar przyjęła prędkość światła w próżni za podstawę definicji metra. Potwierdzeniem STW są też sukcesy opartych na niej teorii grawitacji i cząstek elementarnych[2]. W ten sposób STW zastąpiła wcześniejsze teorie eteru, m.in. podobną do niej teorię eteru Lorentza. Teoria Einsteina wyeliminowała też konkurencyjne teorie emisyjne.
Szczególna teoria względności wywarła również wpływ na popkulturę. Przewidywany przez nią wzór stał się jednym z najbardziej znanych na świecie. Nawiązują do niego m.in. tytuły filmów fabularnych i albumów muzycznych (także polskich). Oprócz tego w twórczości science fiction – m.in. w powieści Powrót z gwiazd Stanisława Lema – pojawia się opisywana przez STW dylatacja czasu i powiązany paradoks bliźniąt, będące formą podróży w przyszłość.
Nazewnictwo[edytuj | edytuj kod]
Termin teoria względności został wprowadzony przez Plancka i Bucherera, a nazwa szczególna teoria względności pojawiła się później, kiedy Einstein pracował nad teorią ogólną[potrzebny przypis]. Wskazywano na niefortunność i potencjalną mylność tego terminu, zwł. w innych językach (niem. Relativitätstheorie, ang. theory of relativity). STW nie ma nic wspólnego z relatywizmem filozoficznym. Stojąca u jej podstaw zasada względności oznacza, że prawa fizyki są niezmiennicze i bezwzględne. Podobnie niezmiennicza jest prędkość światła w próżni, o czym mówi II postulat STW, a także interwał czasoprzestrzenny wprowadzony w geometrycznym formalizmie Minkowskiego[3].
Przesłanki powstania teorii[edytuj | edytuj kod]

Przed XIX wiekiem[edytuj | edytuj kod]
W XVI w. Galileusz i inni zakwestionowali poglądy starożytnych, zwłaszcza Arystotelesa, wierzących w układ preferowany, w którym środek Wszechświata i położona w nim Ziemia spoczywają. Galileusz doszedł do wniosku, że prędkość i położenie ciała są względne. Z każdym przedmiotem można powiązać inny układ odniesienia. Obserwator nieruchomy względem takiego układu odnosi wrażenie, że on jest w spoczynku, podczas kiedy całe otoczenie porusza się, a jednocześnie osoba nieruchoma względem innego układu (np. stojąca na ziemi) dojdzie do zupełnie przeciwnych wniosków. Matematycznym zapisem względności położenia i prędkości jest transformacja Galileusza.
Galileusz był też prekursorem pierwszej zasady dynamiki Newtona. Wierzył – inaczej niż Arystoteles – że ciała swobodne poruszają się ruchem jednostajnym, a nie opóźnionym. Układy odniesienia, w których to zachodzi, nazwano potem układami inercjalnymi. Zgodnie z transformacjami Galileusza, istnienie jednego układu inercjalnego pociąga za sobą istnienie nieskończenie wielu, poruszających się względem niego i siebie nawzajem ze stałą prędkością.
Wśród tych nieskończenie wielu układów odniesienia żaden nie jest wyróżniony – prawa fizyki, np. mechaniki Newtona, przyjmują w nich identyczną postać. Przez to żaden eksperyment nie jest w stanie wskazać, w którym układzie inercjalnym jest obserwator. Ten ostatni fakt nazwano galileuszowską zasadą względności.
XIX i XX wiek[edytuj | edytuj kod]
Przesłanki optyczne[edytuj | edytuj kod]


W XIX wieku nowe badania ujawniły niedoskonałość mechaniki klasycznej. Zgodnie z transformacjami Galileusza oraz długo uznawaną korpuskularną teorią światła Newtona prędkość światła powinna zależeć od wzajemnego ruchu obserwatora i źródła. Obserwacje aberracji gwiazdowej przez François Arago w 1810 nie znalazły żadnych rozbieżności[4].
Obserwacje te wyjaśnił w 1818 roku Augustin Jean Fresnel w ramach falowej teorii światła, która m.in. z tego powodu stała się nowym paradygmatem w optyce. Jednak falowa teoria światła również miała problemy z mechaniką klasyczną. Wprowadzała układ preferowany – eter. W modelu Fresnela niemożliwe było wykrycie go przez aberrację światła i inne doświadczenia pierwszego rzędu – takie, których wyniki zależały od tylko pierwszej potęgi Ruch względem eteru miał być niemożliwy do wykrycia metodami mechanicznymi i optycznymi I rzędu, ale potencjalnie możliwy metodami optycznymi wyższych rzędów – łamiąc zasadę względności Galileusza. Oprócz tego Fresnelowskie wzory na transformację prędkości światła w ośrodku rozbiegały się z transformacjami Galileusza. Eksperyment Fizeau wydawał się potwierdzać model Fresnela (tzw. częściowe wleczenie eteru), naruszając zasadę względności i transformacje Galileusza.
Aby wykryć „wiatr eteru”, wykonano wiele doświadczeń II rzędu, które dały wynik negatywny, z których najbardziej znanym było doświadczenie Michelsona-Morleya z 1887. Okazało się, że – wbrew przewidywaniom fizyki klasycznej – światło biegnie w próżni z taką samą prędkością względem obserwatora niezależnie od układu odniesienia[5], także w II rzędzie.
Przesłanki elektrodynamiczne[edytuj | edytuj kod]
Nie tylko optyka, ale i elektrodynamika wydawała się łamać zasadę względności. Równania Maxwella opisują pole elektromagnetyczne i w swojej pełnej postaci zawierają w prawie Ampère’a człon opisujący prąd przesunięcia. Gwarantuje on zachowanie ładunku i przewiduje fale elektromagnetyczne. Prąd przesunięcia zniszczył symetrię Galileuszowską – transformacje Galileusza zawodziły w tym przypadku. Równania Maxwella wydawały się obowiązywać w tylko jednym układzie odniesienia, który utożsamiono z eterem[6].
Odpowiedzi teoretyczne[edytuj | edytuj kod]
Aby wyjaśnić doświadczenie Michelsona-Morleya, Fitzgerald w 1889 i niezależnie Lorentz w 1891 zaproponowali hipotezę kontrakcji – przyrządy pomiarowe na skutek ruchu względem eteru miały się skracać, co prowadzi do uzyskania zawsze tej samej wartości prędkości światła w próżni. Lorentz rozwinął tę hipotezę, proponując transformacje Lorentza i całą teorię eteru, wyjaśniającą wszystkie dotychczasowe doświadczenia. Oprócz tego te transformacje okazały się symetriami równań Maxwella – potencjalnie ratując zasadę względności w elektrodynamice.
Młody wówczas Albert Einstein prawdopodobnie wiedział o doświadczeniu Michelsona-Morleya[b], pracach Lorentza i Poincarégo. Starał się pogodzić elektrodynamikę Maxwella z zasadą względności Galileusza. Próbował zmodyfikować elektrodynamikę, tak by prowadziła do emisyjnej teorii światła. Kiedy to się nie udało, Einstein postanowił zrewidować podstawy mechaniki[7].
Postulaty szczególnej teorii względności[edytuj | edytuj kod]
Albert Einstein oparł swoje rozumowanie na dwóch postulatach[8]:
- Zasadzie względności
- We wszystkich układach inercjalnych prawa fizyki są jednakowe – zarówno mechaniki, jak i elektrodynamiki.
- Niezmienniczość prędkości światła w próżni
- Dla wszystkich obserwatorów inercjalnych prędkość światła w próżni jest taka sama – we wszystkich kierunkach i nie zależy od prędkości źródła światła.
Alternatywne założenia szczególnej teorii względności, interesujące szczególnie z teoretycznego punktu widzenia, są oparte na następujących, prostszych założeniach:
- Zasada względności: „Wszystkie układy odniesienia poruszające się względem siebie ze stałą prędkością są równoważne”,
- założenie, że transformacja pomiędzy tak określonymi układami jest transformacją afiniczną (liniową).
Powyższe założenia pozwalają wyprowadzić ogólną postać transformacji pomiędzy układami inercjalnymi. Te transformacje okazują się mieć matematyczną postać transformacji Lorentza. Zawierają one w szczególności jeden parametr – stałą o wymiarze odwrotności prędkości. Należy ją interpretować jako odwrotność prędkości granicznej: maksymalnej prędkości, z jaką mogą poruszać się obserwatorzy, stałej we wszystkich inercjalnych układach odniesienia. Zerowa wartość tego parametru oznacza nieskończoną prędkość graniczną (brak prędkości granicznej) i prowadzi do transformacji Galileusza. Jeśli zamiast tego skorzysta się z równań Maxwella, to prędkość graniczna musi być równa prędkości światła w próżni.
Najważniejsze konsekwencje[edytuj | edytuj kod]


Dwa postulaty Einsteina jednoznacznie prowadzą do transformacji Lorentza[2], a one – do dalszych przewidywań. Jeśli prędkości względne są porównywalne do prędkości światła w próżni to fizyczne wnioski z STW są różne od tych z mechaniki Newtona. Prędkość jest nieporównywalnie większa niż te, z którymi ludzie się spotkają na co dzień. Dlatego też niektóre konsekwencje szczególnej teorii względności są początkowo sprzeczne z intuicją:
- Względność jednoczesności – dwa zdarzenia określone przez jednego obserwatora jako jednoczesne, mogą nie być jednoczesne dla innego obserwatora[9][10].
- Dylatacja czasu – czas, jaki mija pomiędzy dwoma zdarzeniami, nie jest jednoznacznie określony, lecz zależy od ruchu obserwatora. Odstępy czasowe między zdarzeniami są większe („czas płynie wolniej”), jeśli obserwator się porusza, a nie spoczywa względem ich położenia. Innymi słowy: jeśli zjawisko – zachodzące w jakimś punkcie przestrzeni – jest obserwowane z układów poruszających się względem tego punktu, to trwa dłużej niż w układzie odniesienia, w którym punkt tego zjawiska spoczywa[11][10].
- Konsekwencją tego zjawiska – w kontekście zawracającego układu inercjalnego – jest paradoks bliźniąt. Został sformułowany przez Langevina[potrzebny przypis] i potem był podnoszony przez Bergsona jako argument przeciwko STW[potrzebny przypis].
- Kontrakcja przestrzeni lub relatywistyczne skrócenie długości, skrócenie Lorentza – odległości między punktami zależą od układu odniesienia. Wszystkie poruszające się przedmioty obserwuje się jako krótsze niż wtedy, gdy spoczywają[2]. Relatywistyczne skrócenie obiektu zawsze wyniesie tyle samo procent dla danej prędkości[12].
- Zjawisko prowadzi do paradoksu drabiny – drabina może mieć długość większą niż długość stodoły, ale zmieścić się w tej stodole w całości, jeżeli drabina będzie poruszała się odpowiednio szybko w układzie spoczynku stodoły.
- Relatywistyczne składanie prędkości[2] – prędkości nie transformują się przez dodawanie do i odejmowanie od względnej prędkości układów odniesienia. Przykładowo: jeżeli rakieta oddala się od obserwatora z prędkością i wysyła pocisk z prędkością w układzie swojego spoczynku, to obserwator nie zanotuje prędkości przewyższającej prędkość światła w próżni. W tym przykładzie obserwator widziałby pocisk poruszający się z szybkością Podobnie przy dwóch strumieniach cząstek poruszających się z prędkością bliską – jedne emitowane na lewo od źródła, drugie na prawo – z perspektywy jednych cząstek drugie nie będą uciekały szybciej niż [13].
- Wartości innych wielkości fizycznych – takich jak przyspieszenie, siła, gęstość optyczna czy natężenie pola elektrycznego – zależą od ruchu obserwatora, mimo że w mechanice klasycznej są niezmiennicze dla układów inercjalnych. Niektórzy autorzy, zwłaszcza dawniejsi, wprowadzają też pojęcie masy relatywistycznej[2].
- Wartości niektórych wielkości fizycznych, np. pędu czy energii kinetycznej, transformują się inaczej niż w mechanice klasycznej.
- Siła Lorentza w elektrodynamice może być wyprowadzona z STW i z prawa Coulomba.
- Efekt Dopplera dla fal elektromagnetycznych[2] jest symetryczny, tzn. nie uwzględnia prędkości obserwatora i źródła względem ośrodka, a jedynie względem siebie nawzajem. Jest opisany innym wzorem niż dla fal akustycznych – będącym średnią geometryczną wzorów dla ruchu obserwatora i dla ruchu źródła w mechanice klasycznej. Relatywistyczne współczynniki dopplerowskie są wartościami własnymi liniowego przekształcenia Lorentza (i odpowiedniej macierzy). Relatywistyczny efekt Dopplera obejmuje też efekt poprzeczny, kiedy fale i obserwator poruszają się w prostopadłych kierunkach. Analogiczny efekt nie występuje w mechanice klasycznej.
- Masa jest równoważna energii[2], a związek między tymi wielkościami opisuje wzór Zwiększenie energii układu zwiększa jego masę, zmniejszenie energii powoduje zmniejszenie masy. I odwrotnie – ubytek masy oznacza ubytek energii układu (por. deficyt masy)[14].
- Ograniczenie prędkości – STW przewiduje, że:
- Jeśli w jakimś układzie inercjalnym dwa ciała poruszają się z prędkościami podświetlnymi (mniejszymi niż ), to względem siebie również poruszają się z prędkością podświetlną.
- Dla ciał z niezerową masą niemożliwe jest osiągnięcie prędkości – zgodnie z zasadą zachowania energii.
- Dla ciał bezmasowych (jak fotony, gluony, grawitony itp., zwane zbiorczo luksonami) prędkość jest jedyną możliwą.
- Gdyby istniały cząstki nadświetlne, tzn. z prędkością większą niż (tzw. tachiony), ich masa lub energia byłyby wyrażone liczbami urojonymi, pozbawionymi sensu fizycznego.
- W nadświetlnych układach odniesienia kolejność przyczyn i skutków byłaby odwrócona, łamiąc przyczynową strzałkę czasu.
- Co ważne – ograniczenie prędkości dotyczy tylko konkretnych, indywidualnych ciał, przenoszących energię i informację. Nie dotyczy procesów wynikających z ruchu wielu ciał, nieprzenoszących energii ani informacji, np. niektórych rodzajów fal. Dlatego prędkość fazowa i prędkość grupowa fal elektromagnetycznych w niektórych materiałach mogą przekraczać nie łamiąc STW[15].
- Ograniczenie prędkości nie dotyczy też samej czasoprzestrzeni, dlatego nadświetlne prędkości mogą być osiągane przez ucieczkę galaktyk (Prawo Hubble’a-Lemaître’a), napęd Alcubierre’a czy tunel czasoprzestrzenny.
- Zdaniem Einsteina w mechanice kwantowej kolaps wektora stanu (funkcji falowej) w wyniku pomiaru układu splątanego łamie ograniczenie prędkości z STW – mówi o tym paradoks EPR. Jednak zdaniem Heisenberga i większości fizyków taki pomiar jest zgodny z STW, ponieważ jego wynik jest losowy i nie może posłużyć do przekazywania energii ani informacji[potrzebny przypis]. Podobnie propagatory w kwantowej teorii pola sugerują prędkości nadświetlne, jednak nie prowadzą do przesyłu energii ani informacji.
- STW prowadzi też do innych efektów, których Einstein nie przewidział, np. precesja Thomasa dla ruchu dwuwymiarowego oraz paradoks Bella i efekt Unruha dla układów przyspieszających. Za konsekwencje STW można też uznać efekty odróżniające relatywistyczną mechanikę kwantową od zwykłej, nierelatywistycznej – jak konieczne istnienie spinu oraz antymaterii.
Dokładniejszy opis konsekwencji[edytuj | edytuj kod]
Składanie prędkości[edytuj | edytuj kod]

Dylatacji czasu zawsze towarzyszy kontrakcja przestrzeni. Przez to transformacja Lorentza prowadzi do praw składania prędkości innych niż dla transformacji Galileusza. Można założyć, że dany obserwator inercjalny widzi ciało poruszające się wzdłuż osi zgodnie z jej zwrotem, z prędkością
Niech obserwator porusza się względem niego z prędkością w tym samym kierunku mierząc odpowiednie współrzędne przestrzenne jako Układ obserwuje prędkość tego ruchomego ciała jako
Można ją wyrazić przez prędkości oraz
Analogiczna jest transformacja odwrotna – wyrażająca prędkość dla obserwatora przez tę Opisuje ją wzór:
To prawo składania prędkości jest zgodne z II postulatem STW – niezmienniczością prędkości światła w próżni. Niech w jednym układzie inercjalnym jakieś ciało (foton, gluon, grawiton lub inny lukson) porusza się z prędkością W drugim układzie inercjalnym – poruszającym się z prędkością względem pierwszego – ciało również będzie się poruszać z prędkością
Przykład[edytuj | edytuj kod]
Z Ziemi wysyłana jest duża stacja badawcza do badania kosmosu i osiąga ona prędkość względem Ziemi. Ze stacji tej wysyłana jest sonda badawcza i porusza się ona w tym samym kierunku, z prędkością względem stacji badawczej.
Według mechaniki klasycznej (transformacji Galileusza) prędkość sondy względem Ziemi miałaby wartość Prędkość sondy przekraczałaby prędkość światła w próżni, zatem obliczenie jest błędne. Poniżej prawidłowe obliczenie, zgodne z STW.
Niech układ primowany oznacza układ odniesienia związany z Ziemią, a układ nieprimowany niech będzie związany ze stacją badawczą. Wówczas wzór na składanie prędkości będzie miał postać:
a po podstawieniu wartości liczbowych daje:
Prędkość ta jest mniejsza od prędkości światła w próżni Złożenie dwóch dowolnych prędkości mniejszych od da zawsze prędkość mniejszą od [potrzebny przypis].
Równoważność masy i energii[edytuj | edytuj kod]

Energia spoczynkowa[edytuj | edytuj kod]
Prawdopodobnie najsłynniejszą implikacją szczególnej teorii względności jest wniosek, że masa jest formą energii.
Wcześniej uważano, że masa ciała jest wielkością stałą i addytywną, tzn. masa całości jest sumą mas jej części, niezależnie od energii oddziaływań między nimi. W procesach z udziałem wielu ciał, np. w zderzeniach i reakcjach chemicznych, masa miała być bezwzględnie zachowana. Za to energia – kinetyczna i potencjalna – miały być wielkościami wtórnymi, zależnymi od masy ciała, która jednak była od nich niezależna. Podobnie zasada zachowania energii miała być niezależna od zachowania masy.
Jednak Einstein w pracy z 1905 przewidział, że zmiana energii obiektu wpływa na jego bezwładność, zgodnie z równaniem:
gdzie:
- – energia ciała w spoczynku (energia spoczynkowa),
- – jego masa spoczynkowa,
- – prędkość światła w próżni.
Oznacza to, że zasada zachowania masy – w przeciwieństwie do zachowania energii – nie musi obowiązywać bezwzględnie. W szczególności: odkryto, że nie obowiązuje w reakcjach jądrowych ani w reakcjach cząstek elementarnych. Przykładowo anihilacja cząstek i antycząstek prowadzi do całkowitej zamiany masy w energię bezmasowych fotonów. Za to kreacja par polega na zamianie wysokich energii kinetycznych w masy cząstek, także ciężkich jak higgs. Oprócz tego masa nie jest addytywna i np. w jądrach atomowych występuje znaczny deficyt masy, ze względu na wysoką energię potencjalną oddziaływań silnych między nukleonami.
Z powyższego równania wynika wzór na energię spoczynkową ciała: STW nie przewiduje jednoznacznie energii spoczynkowej, tzn. nie wskazuje wartości tej stałej[potrzebny przypis]. Jednak okazuje się, że dla wszystkich obiektów jest to najprostsza zależność (stała wynosi zero):
Energia kinetyczna[edytuj | edytuj kod]
Oprócz tego STW podaje nowy wzór na energię obiektu w ruchu. Jeśli ciało porusza się z prędkością względem obserwatora, to jego całkowita energia wynosi:
gdzie:
Parametr (mieszczący się w przedziale od 0 włącznie do 1 wyłącznie, ) wyraża prędkość ciała w jednostkach naturalnych. Parametr nazywany jest czynnikiem Lorentza lub współczynnikiem relatywistycznym[c]. Za to wielkość jest tzw. masą relatywistyczną, odrzucaną przez część autorów.
Gdy jest dużo mniejsze od równanie można uprościć do:
Przyjmując, że pierwszy człon odpowiada energii wewnętrznej ciała, dochodzi się do „zwykłego” wzoru na całkowitą energię ciała w ruchu. Drugi człon jest równy „normalnej” energii kinetycznej, wynikającej z newtonowskiej mechaniki klasycznej. Przejście to wynika z rozwinięcia czynnika w szereg Maclaurina w otoczeniu punktu
Ograniczenie prędkości[edytuj | edytuj kod]
Przy bardzo dużej prędkości, zbliżonej do mianownik wyrażenia na zaczyna dążyć do 0, a sama wartość dąży do nieskończoności:
Wynika z tego, że przy prędkości światła w próżni energia ciała posiadającego niezerową masę powinna być nieskończona, czyli praktycznie nie istnieje możliwość rozpędzenia go do tej prędkości. Oznacza to, że żadna cząstka nie może zostać rozpędzona do prędkości światła w próżni, a tym bardziej przekroczyć jej. Prędkość tę mogą osiągnąć tylko cząstki bezmasowe (fotony, gluony, grawitony, w ogólności luksony). Jednak dla nich prędkość jest jedyną możliwą – nie mogą jej przekroczyć ani poruszać się wolniej[potrzebny przypis].
Tachiony to hipotetyczne cząstki, które mogłyby się poruszać z prędkością większą od światła w próżni. Miałyby paradoksalne własności jak urojona masa lub energia. W ich układzie odniesienia odwrócona byłaby kolejność przyczyn i skutków, czyli mogłyby podróżować wstecz w czasie (dając tachionowy antytelefon). Istnieją teorie postulujące ich istnienie[potrzebny przypis]. Jak dotąd nie zaobserwowano żadnych zjawisk świadczących o ich istnieniu.
Od czasu do czasu pojawiają się doniesienia o przekroczeniu prędkości światła w próżni przez różne obiekty. Ostatnio miało to miejsce 23 września 2011 roku (eksperyment OPERA). Jak dotąd żadne z tych doniesień nie zostało potwierdzone.
Formalizm czasoprzestrzeni Minkowskiego[edytuj | edytuj kod]

Diagram czasoprzestrzenny[edytuj | edytuj kod]
W STW do opisu zjawisk fizycznych stosowana jest czterowymiarowa czasoprzestrzeń, w której chwilowe położenia ciała punktowego są nazywane zdarzeniami. Zmiany położenia obiektu układają się w linię ciągłą, nazywaną linią świata[6]. Ciało takie może posiadać parametry fizyczne jak masę, ładunek, energię, pęd itd., które nie są bezpośrednio uwzględniane w takim opisie.
Czasoprzestrzeń jest czterowymiarowa, zatem współrzędne zdarzenia określone są przez czwórkę liczb. W takim układzie współrzędnych jedna z osi odpowiada czasowi, a pozostałe – współrzędnym przestrzennym. W użyciu jest kilka wersji takiego opisu. A. Einstein używał tradycyjnej konwencji kartezjańskiego układu współrzędnych oraz czasu Minkowski wprowadził czasoprzestrzeń z czasem urojonym: gdzie Obecnie często używa się konwencji gdzie lub gdzie
Można stosować układ jednostek SI i wtedy czas jest mierzony w sekundach, a położenie – w metrach. Można również uproszczać wzory przez jednostki naturalne, w których prędkość światła w próżni jest wielkością bezwymiarową i równą 1. Czas jest tam mierzony w metrach świelnych lub przeciwnie – odległość jest mierzona w sekundach świetlnych.
By przedstawić czasoprzestrzeń graficznie, na rysunkach pomija się co najmniej jeden wymiar przestrzenny. Oś odpowiadającą czasowi skaluje się odpowiednio do rysunku, zazwyczaj w jednostkach (rysunek stożka świetlnego).
Obserwator stale porusza się wzdłuż linii świata, zgodnie ze zwrotem osi czasowej, nawet jeśli stoi w miejscu w zwykłej przestrzeni. Liniami świata punktu materialnego, na który nie działa żadna siła, jest linia prosta w czasoprzestrzeni. Odpowiada to pierwszej zasadzie dynamiki Newtona znanej z mechaniki klasycznej.
Wszystkie linie świata światła wysłanego z jednego punktu w jednej chwili spełniają wspólne równanie. Odpowiada ono równaniu powierzchni stożka, którego osią jest oś czasu, tyle że w przestrzeni czterowymiarowej. Powierzchnię tę nazywa się stożkiem świetlnym światła wychodzącego. Podobnie wszystkie promienie świetlne docierające do punktu w jednej chwili tworzą powierzchnię stożka, a powierzchnia ta jest nazywana stożkiem świetlnym światła przychodzącego.
Postulaty i transformacje[edytuj | edytuj kod]

Różni obserwatorzy (układy odniesienia) opisują czasoprzestrzeń Minkowskiego za pomocą innych współrzędnych. Dwa postulaty STW można wyrazić w języku geometrii i transformacji między tymi układami.
- Jeśli w jednym z tych układów odniesienia linią świata obiektu jest linia prosta, to w innych też jest nią linia prosta.
- Linie świata światła są nachylone zawsze pod takim samym kątem do osi czasu, w każdym inercjalnym układzie odniesienia.
Pierwszy postulat wyraża zasadę względności – każdy z postulowanych układów odniesienia musi być inercjalny i żaden z nich nie może być wyróżniony. Drugi postulat mówi w języku geometrii o stałej prędkości światła w próżni dla każdego inercjalnego obserwatora.
Przy wyżej opisanych założeniach (zasada względności i niezmienność prędkości światła w próżni) okazuje się, że różni obserwatorzy obserwują to samo zdarzenie w różnych momentach czasowych i w różnych punktach przestrzennych. Zasady przeliczania (transformacji) współrzędnych obserwatorów poruszających się wzdłuż osi x określa transformacja Lorentza[2]:
Jak napisano w poprzednich sekcjach – z tych transformacji wynikają wszystkie efekty relatywistyczne, np. dylatacja czasu i kontrakcja przestrzeni.
Interwał czasoprzestrzenny[edytuj | edytuj kod]

Transformacja Lorentza nie zmienia wartości interwału czasoprzestrzennego s[2]
lub
tzn. jest on jednakowy dla wszystkich inercjalnych obserwatorów.
Uwaga: także liczba przeciwna do powyższej jest stała. Dlatego to ją można przyjąć za definicję interwału czasoprzestrzennego. Wtedy odpowiednia forma kwadratowa ma inną sygnaturę[potrzebny przypis].
Czasoprzestrzeń z tak określonym niezmiennikiem nazywana jest czasoprzestrzenią Minkowskiego[2]. Interwał odpowiada odległości w „zwykłej” przestrzeni (przestrzeń Euklidesa). Tak jak odległość – ma on pewne własności metryki: jest funkcją symetryczną i spełniającą nierówność trójkąta. Mimo to są między nimi istotne różnice:
- Odległość różnych punktów jest liczbą większą lub równą zeru – metryka przyjmuje nieujemne wartości. Za to interwał czasoprzestrzenny może być dowolną liczbą rzeczywistą, także ujemną.
- Jeśli odległość dwóch punktów wynosi zero, to są one tym samym punktem – mówi się, że metryka jest niezdegenerowana. Za to interwał czasoprzestrzenny wynosi zero między dowolnymi dwoma punktami na stożku świetlnym.
Z tego powodu czasami interwał nie jest metryką, ale pseudometryką, a czasoprzestrzeń Minkowskiego – przestrzenią pseudoeuklidesową[potrzebny przypis]. Z tej perspektywy transformacje Lorentza są izometriami czasoprzestrzeni Minkowskiego, a grupa Lorentza i grupa Poincarégo są grupami izometrii.
Można też z góry postulować pseudometrykę czasoprzestrzeni Minkowskiego, a znajdując dla niej grupę izometrii – otrzymać transformacje Lorentza, bez odwołania do dwóch postulatów STW[potrzebny przypis].
Klasyfikacja interwałów ze względu na znak (dla konwencji ):
(1) interwał czasopodobny
– dotyczy zdarzeń, które są powiązane przyczynowo ze sobą, bo może przejść oddziaływanie od jednego zdarzenia do drugiego, poruszające się z prędkością światła lub mniejszą.
Mówi się, że punkt B jest położony czasowo względem punktu A, jeżeli leży wewnątrz stożka świetlnego punktu A lub na jego powierzchni. Przy tym obszar „górnego” stożka to absolutna przyszłość punktu A, a obszar „dolnego” stożka – jego absolutna przeszłość.
(2) interwał przestrzennopodobny
– dotyczy zdarzeń, które nie są powiązane przyczynowo ze sobą, bo nie może przejść oddziaływanie od jednego zdarzenia do drugiego, poruszające się nawet z prędkością światłą.
Na rysunku punkt C jest położony przestrzennie względem punktu A, bo leży poza stożkiem światła punktu A. Dla punktów położonych przestrzennie można znaleźć układ odniesienia, w którym oba zdarzenia występują jednocześnie, a w innych – jedno może być wcześniej lub później niż drugie. Dlatego cały obszar poza stożkami świetlnymi nazywa się względną teraźniejszością.
(3) interwał zerowy
– dotyczy zdarzeń, które są powiązane przyczynowo ze sobą, bo może przejść oddziaływanie od jednego zdarzenia do drugiego, poruszające się z prędkością światła. Każdy punkt leżący na powierzchni stożka świetlnego ma położenie zerowe względem początku układu.
Nierówność trójkąta dla interwału czasoprzestrzennego pozwala na eleganackie wyjaśnienie paradoksu bliźniąt[potrzebny przypis].
Względność jednoczesności[edytuj | edytuj kod]


W teorii względności istnieją pojęcia „ścieżki czasowej” i „ścieżki przestrzennej” w czasoprzestrzeni. Gdy jakiś obiekt porusza się ze stałą prędkością razem z obserwatorem, to wówczas obserwator w swoim układzie odniesienia odczuwa tylko upływ czasu, a nie ma możności zaobserwowania ruchu obiektu. Trasa, jaką pokonuje taki obiekt, definiuje pojęcie „ścieżki czasowej”. Można też sobie wyobrazić trasę w czasoprzestrzeni, wzdłuż której obserwator nie odczuwa upływu czasu, a jedynie przemieszczanie się w przestrzeni. To właśnie jest ścieżka przestrzenna. Biorąc pod uwagę, że maksymalna prędkość, jaką można osiągnąć, to prędkość światła w próżni, można łatwo dowieść, że każdy prosty odcinek między takimi dwoma punktami w czasoprzestrzeni, którego nie można przebyć w skończonym czasie, jest ścieżką przestrzenną. Obiekty połączone taką ścieżką nie mogą na siebie w żaden sposób oddziaływać fizycznie ani siebie wzajemnie obserwować.
Jeżeli dwaj obserwatorzy i znajdują się w dwóch różnych układach odniesienia, między którymi istnieje ścieżka czasowa, i obserwują oni dwa różne zdarzenia A i B, między którymi istnieje tylko ścieżka przestrzenna, wówczas, stosując szczególną teorię względności, można dowieść, że dla obu obserwatorów zdarzenia i mogą następować w różnej kolejności czasowej. Obserwator może widzieć zdarzenie jako pierwsze, zaś obserwator może widzieć zdarzenie B jako pierwsze.
Wynika stąd, że również pojęcie równoczesności jest względne. Jeżeli jakieś dwa zdarzenia są równoczesne dla jednego obserwatora, wcale nie muszą być takie dla innego obserwatora.
Ograniczenie prędkości. Zasada przyczynowości[edytuj | edytuj kod]
Oddziaływania fizyczne mogą rozchodzić się z maksymalną prędkością równą prędkości światła. Dlatego żadne zdarzenie nie może mieć wpływu na zdarzenie leżące poza stożkiem świetlnym – określa to zasadę przyczynowości. Gdyby zasada ta nie obowiązywała, to dane zdarzenie mogłoby wpłynąć na zdarzenia z przeszłości.
Dla przykładu jeżeli w punkcie A wybuchnie supernowa, to obserwator w punkcie B ją dostrzeże, ale ten w punkcie C już nie będzie widział eksplozji. Zjawisko to jest podobne do sytuacji człowieka stojącego na powierzchni Ziemi. Nie widzi on niczego, co dzieje się poza horyzontem, mimo że coś tam się znajduje. Powierzchnia stożka świetlnego odpowiada właśnie linii tego horyzontu w czasoprzestrzeni. Podobnie jak obserwator na Ziemi, ten w punkcie C może się przemieścić. Wniosek ten jest zgodny z codziennym doświadczeniem. Astronomowie nie mogą obserwować odległych gwiazd w stanie aktualnym (jednoczesnym według nas). Ale obserwują światło gwiazd wyemitowane wiele lat temu (np. jeżeli gwiazda alfa Centauri odległa jest od nas o 4 lata świetlne, to obserwując ją, widzimy ją w stanie, w jakim była 4 lata temu).
Ograniczenie prędkości ciał można wyrazić matematycznie. Linie świata są nie tylko funkcjami ciągłymi, ale i lipschitzowskimi – ich iloraz różnicowy jest ograniczony przez stałą [potrzebny przypis].
STW a inne teorie[edytuj | edytuj kod]
Elektrodynamika[edytuj | edytuj kod]
STW była inspirowana m.in. klasyczną elektrodynamiką Maxwella. Pozwoliła wyprowadzić wzór na siłę Lorentza, wcześniej postulowany arbitralnie, na podstawie doświadczenia[potrzebny przypis].
Ze względu na symetrię lorentzowską równań Maxwella, można je zapisać w sposób tensorowy i jawnie kowariantny (niezmienniczy). W takich równaniach osobne współrzędne przestrzenne i czasowe są zastąpione przez czterowektor położenia w czasoprzestrzeni Minkowskiego. Osobne pola elektryczne i magnetyczne są zastąpione przez tensor pola elektromagnetycznego. Odpowiadające im potencjały są wyrażone przez czteropotencjał, a oddziałujące z nimi ładunki i prądy – przez czterowektor gęstości prądu elektrycznego. To redukuje liczbę równań Maxwella do dwóch, ponieważ prawo Gaussa dla elektryczności można połączyć z prawem Ampère’a, a prawo Gaussa dla magnetyzmu – z prawem Faradaya.
STW pozwala też sformułować elektrodynamikę w sposób jeszcze prostszy, wolny od współrzędnych i indeksów – za pomocą form różniczkowych na czasoprzestrzeni[potrzebny przypis].
Grawitacja[edytuj | edytuj kod]
Po opublikowaniu STW rozwinęły się prace nad relatywistycznymi teoriami grawitacji, uwzględniającymi ograniczenie prędkości oddziaływań. Oprócz tego w 1907 Hermann Minkowski sformułował STW w języku płaskiej czasoprzestrzeni. Einstein zaakceptował pomysł Minkowskiego i zrozumiał, że relatywistyczną teorię grawitacji można sformułować za pomocą ogólniejszych, zakrzywionych czasoprzestrzeni.
Wreszcie w 1915 roku Einstein opracował, a w 1916 opublikował ogólną teorię względności – rozszerzającą STW o opis zjawisk zachodzących w obecności pola grawitacyjnego[6]. Zasada równoważności mówi, że układy odniesienia spadające swobodnie są lokalnie inercjalne. To pozwala na uogólnienie zasady względności z układów inercjalnych także na niektóre nieinercjalne – mianowicie te spadające swobodnie. Ogólna teoria względności opiera się nie tylko na zasadzie równoważności i uogólnieniu zasady względności z STW. Pozostałe filary to zasada korespondencji postulująca uogólnienie prawa powszechnego ciążenia oraz zasady zachowania[potrzebny przypis].
Fizyka kwantowa[edytuj | edytuj kod]
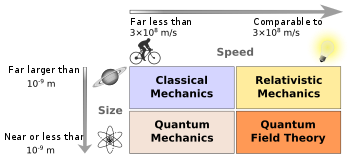
STW zastosowano nie tylko do klasycznej elektrodynamiki i grawitacji, ale również do mechaniki kwantowej. W 1916 roku Sommerfeld zastosował teorię Einsteina do modelu atomu Bohra, poprawiając jego zgodność z doświadczeniem. Dalsze prace przyszły po sformułowaniu właściwej mechaniki kwantowej w 1926 przez Heisenberga, Schrödingera i Borna. Już w 1926 sformułowano równanie Kleina-Gordona, a w 1928 – równanie Diraca. Dirac stworzył w ten sposób relatywistyczną mechanikę kwantową, a później sformułowano również kwantowe teorie pola.
Jednocześnie sam Einstein był sceptycznie nastawiony do kompletności mechaniki kwantowej i do jej pełnej zgodności z STW, proponując w 1935 roku paradoks EPR. STW jest trudna do pogodzenia z mechaniką Bohma, co jest jednym z powodów niepopularności tej interpretacji mechaniki kwantowej[potrzebny przypis].
Zobacz też[edytuj | edytuj kod]
Uwagi[edytuj | edytuj kod]
- ↑ Spekulowano o tym, że współautorką STW mogła być pierwsza żona Alberta Einsteina – Mileva Marić – jednak te hipotezy zostały odrzucone. Oprócz tego za współtwórcę STW podaje się czasami francuskiego matematyka Henri Poincarégo. Rozwinął on teorię eteru Lorentza i wprowadził wiele elementów późniejszej STW. Mógł mieć wpływ na prace Einsteina, jednak ostatecznie ich nie zaakceptował[potrzebny przypis].
- ↑ Einstein w latach 20., na wykładzie w Kioto, miał wspomnieć, że przy rozwijaniu STW wiedział o doświadczeniu Michelsona-Morleya. Później, w latach 50., udzielał wywiadu Shanklandowi, pytającemu m.in. o genezę STW. Einstein nie potrafił sobie przypomnieć, czy wtedy wiedział o tym doświadczeniu – sugerując, że nie. Ta druga opinia, sprzeczna z pierwszą, doprowadziła do licznych nieporozumień i badań nad genezą STW. Jednocześnie wskazała, że wyjaśnienie doświadczenia Michelsona-Morleya nie było główną motywacją Einsteina[potrzebny przypis].
- ↑ Czynnik pojawia się często w teorii względności i pochodzi jeszcze z teorii eteru Lorentza.
Przypisy[edytuj | edytuj kod]
- ↑ szczególna teoria względności, [w:] Encyklopedia PWN [dostęp 2022-11-28].
- ↑ a b c d e f g h i j k Trautman 1969 ↓, s. 586.
- ↑ Sokołowski 2015 ↓.
- ↑ What a drag: Arago’s Experiment (1810), dostęp 2017-11-11.
- ↑ Heller i Pabjan 2014 ↓, s. 39.
- ↑ a b c Trautman 1969 ↓, s. 585.
- ↑ John D. Norton, How Einstein did not discover, s. 254.
- ↑ Heller i Pabjan 2014 ↓, s. 40.
- ↑ Heller i Pabjan 2014 ↓, s. 41–42.
- ↑ a b Trautman 1969 ↓, s. 585–586.
- ↑ Heller i Pabjan 2014 ↓, s. 44.
- ↑ Heller i Pabjan 2014 ↓, s. 42–43.
- ↑ Heller i Pabjan 2014 ↓, s. 44–45.
- ↑ Heller i Pabjan 2014 ↓, s. 45–46.
- ↑ Dragan ↓.
Bibliografia[edytuj | edytuj kod]
- Andrzej Dragan: Niezwykle szczególna teoria względności. [dostęp 2017-07-12]. – przystępnie napisany skrypt STW (PDF).
- Michał Heller, Tadeusz Pabjan: Elementy filozofii przyrody. Kraków: Copernicus Center Press, 2014, s. 39–46. ISBN 978-83-7886-065-5.
- Leszek Sokołowski: Relatywizm i niezmienniki. Centrum Kopernika Badań Interdyscyplinarnych w Krakowie, oficjalny kanał na YouTube, 2015-12-09. [dostęp 2017-11-11].
- Andrzej Trautman: Względności teoria. W: Wielka encyklopedia powszechna PWN. Wyd. I. T. 12. Warszawa: Państwowe Wydawnictwo Naukowe, 1969, s. 585–586.
Linki zewnętrzne[edytuj | edytuj kod]
- Polskojęzyczne
- Andrzej Krasiński. Jak powstawała teoria względności. „Postępy Fizyki”. 54 (3), 2003. [zarchiwizowane z adresu].
- Jan Pluta, Podstawy STW, wazniak.mimuw.edu.pl, 2006-09-28, [dostęp 2017-11-14]
- Tomasz Sowiński, wykłady w Centrum Fizyki Teoretycznej PAN, oficjalny kanał na YouTube:
- Wprowadzenie do szczególnej teorii względności– część I, 2015-12-16, [dostęp 2017-11-11]
- Wprowadzenie do szczególnej teorii względności – część II, 2015-12-16, [dostęp 2017-11-11]
- Klasyczne paradoksy szczególnej teorii względności, 2016-01-25, [dostęp 2017-11-11]
- Andrzej Szymacha: Szczególna Teoria Względności – 100 lat później. 2005. [dostęp 2014-07-31]. [zarchiwizowane z tego adresu (2006-01-09)].
- Andrzej Kajetan Wróblewski, Fizyka około roku 1900, slajdy 127–171 [dostęp 2017-11-11].
- Andrzej Kajetan Wróblewski, Einstein dla laików – 100 lat Ogólnej Teorii Względności, wykład z serii „Zapytaj fizyka” na Wydziale Fizyki Uniwersytetu Warszawskiego, oficjalny kanał na YouTube, [dostęp 2017-11-11] – popularny wykład o podstawach STW i OTW
- Anglojęzyczne
- O elektrodynamice ciał w ruchu. Tłumaczenie angielskie pracy Einsteina
- zeskanowane rękopisy Alberta Einsteina. [dostęp 2014-07-31]. [zarchiwizowane z tego adresu (2012-02-05)]. (ang.).
- Michel Janssen, John Stachel, The optics and electrodynamics of moving bodies, 2004 [dostęp 2017-11-11].
- Andrzej Kajetan Wróblewski, Physics around 1900, slajdy 153–217 [dostęp 2017-11-11].
 Don Lincoln, What is relativity all about?, kanał Fermilabu na YouTube, 24 stycznia 2018 [dostęp 2023-05-22].
Don Lincoln, What is relativity all about?, kanał Fermilabu na YouTube, 24 stycznia 2018 [dostęp 2023-05-22].
- Inne


















































































