Efekt Coriolisa

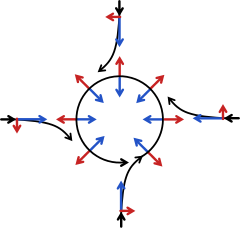
2. Dla obserwatora na tarczy kulka porusza się po zakrzywionym torze. Ruch ten można wyjaśnić jako efekt siły Coriolisa (rys. dolny)
Efekt Coriolisa, powszechnie siła Coriolisa – zjawisko występujące, gdy ciało porusza się w obracającym się układzie odniesienia.
Opis[edytuj | edytuj kod]
Załóżmy, że obserwator nieruchomy względem inercjalnego układu odniesienia obserwuje ciało, na które nie działa żadna siła. Zgodnie z I zasadą dynamiki, ciało to poruszać się będzie ruchem jednostajnym i prostoliniowym – jednak obserwator nieruchomy względem obracającego się nieinercjalnego układu odniesienia będzie widział zakrzywienie toru ruchu ciała. Zakrzywienie to zdaje się być wywołane jakąś siłą, nazwaną siłą Coriolisa. Jest to więc siła pozorna i działa jedynie na ciała poruszające się względem obracającego się nieinercjalnego układu odniesienia.
Badaniem tego zjawiska zajmował się francuski inżynier i matematyk Gaspard-Gustave Coriolis. Efektownym potwierdzeniem siły Coriolisa dla Ziemi jest zmiana płaszczyzny wahania wahadła Foucaulta. Samo zjawisko znali już w XVII wieku włoscy uczeni G.B. Riccioli i F.M. Grimaldi. Równanie je opisujące wyprowadził szwajcarski uczony Leonhard Euler w 1749 roku.
Siła Coriolisa wyrażona jest wzorem:
Z siłą tą wiąże się przyspieszenie Coriolisa[1]:
gdzie:
- – masa ciała,
- – jego prędkość,
- – prędkość kątowa układu,
- – iloczyn wektorowy.
Przyczyny i skutki[edytuj | edytuj kod]
Siła Coriolisa powoduje odchylenie od linii prostej toru ruchu ciała, poruszającego się w układzie obracającym się (np. Ziemi lub płaskiej tarczy). Ponieważ Ziemia obraca się z zachodu na wschód, zatem siła Coriolisa powoduje odchylenie w kierunku zachodnim toru ciała poruszającego się po powierzchni Ziemi ku równikowi (oddala od osi obrotu), a w kierunku wschodnim (przybliża do osi obrotu), gdy ciało porusza się w stronę bieguna, czyli ku miejscu przechodzenia osi obrotu Ziemi.
W drugim szczególnym przypadku na Ziemi siła Coriolisa powoduje odchylenie swobodnie spadających ciał w kierunku wschodnim. Dzieje się tak, gdyż ciało, przybliżając się do osi obrotu, zachowuje swoją dotychczasową prędkość liniową (która jest większa niż dla punktów położonych niżej, obracających się z tą samą prędkością kątową). Jeśli na równiku postawić wysoką wieżę i puścić z jej szczytu swobodnie kamień, to – przyciągany siłą grawitacji – będzie się on zbliżał do powierzchni, która porusza się z mniejszą prędkością liniową niż wierzchołek wieży; zatem spadający kamień „wyprzedzi” powierzchnię Ziemi. Ciała swobodnie spadające odchylają się na wschód wszędzie poza biegunami Ziemi.
Siła Coriolisa nie oddziałuje na ciała pozostające w spoczynku, jak również na ciała poruszające się równolegle do osi obrotu Ziemi (wówczas iloczyn wektorowy prędkości ciała i prędkości kątowej Ziemi równy jest 0).
Efekt na Ziemi[edytuj | edytuj kod]

Ziemia obraca się wokół swojej osi i dlatego dla ciał poruszających się po powierzchni Ziemi, w jej wodach lub atmosferze występuje efekt Coriolisa. Na północ od równika powoduje on zakrzywienie toru ruchu poruszających się obiektów w prawo (z punktu widzenia poruszającego się obiektu), a na południe – w lewo.
Efekt ten nie jest zazwyczaj odczuwalny, objawia się jedynie przy długotrwałych procesach lub w przypadku ciał poruszających się swobodnie na dużym obszarze (pasaty, prądy morskie). A oto przykłady jego wpływu (z punktu widzenia obserwatora poruszającego się wraz z obiektem – wiatrem, rzeką...):
- na półkuli północnej wiatr ma tendencję do skręcania w prawo, a na południowej w lewo,
- na półkuli północnej mocniej podmywane są prawe brzegi rzek, a na południowej lewe[2][3],
- na półkuli północnej cyklony poruszają się odwrotnie do ruchu wskazówek zegara, a na południowej zgodnie z nim,
- płaszczyzna, w której porusza się wahadło, ulega skręceniu na półkuli północnej w prawo, a na południowej w lewo.
Jeśli z określonego miejsca na półkuli północnej zacznie przemieszczać się ku biegunowi masa powietrza, to napływa ona nad obszary o malejącej prędkości liniowej i będzie w stosunku do nich napływać nie z południa, lecz z południowego zachodu. Z punktu widzenia obserwatora na Ziemi wygląda to, jakby na powietrze działała siła skierowana z zachodu na wschód. Tą pozorną siłą jest właśnie siła Coriolisa.
Efekt Coriolisa musi być także brany pod uwagę przez artylerzystów, osoby sterujące lotem samolotów, rakiet itp.
Przykłady[edytuj | edytuj kod]
- Ciało upuszczone ze szczytu wieży Eiffla (wysokość 273 m z najwyższego tarasu) spadnie przesunięte o 6,5 cm na wschód (nie uwzględniając innych sił)[a].
- Pocisk wystrzelony z 50 stopnia szerokości geograficznej północnej lecący z przeciętną prędkością poziomą 1800 m/s w kierunku południkowym (na północ lub na południe), w ciągu 20 sekund lotu (na 36 km) zboczy o około 40 metrów od celu, nie uwzględniając wpływu wiatru, ruchu obrotowego pocisku, zmiany sił działających na niego w wyniku zmiany kierunku ruchu[b].
Zobacz też[edytuj | edytuj kod]
- fale Rossby’ego
- lewoskrętność, prawoskrętność
- parametr Coriolisa
- siła Coriolisa-Stokesa
- siła odśrodkowa
- transwersalna siła bezwładności
Uwagi[edytuj | edytuj kod]
- ↑ Przy spadku swobodnym siła Coriolisa zmienia się w czasie, więc przesunięcie określa wzór (wyprowadzenie):
- – szerokość geograficzna.
- ↑ Przesunięcie przy poziomym ruchu wzdłuż południka określa wzór (źródło):
Przypisy[edytuj | edytuj kod]
- ↑ Siła Coriolisa, [w:] Encyklopedia PWN [dostęp 2021-07-22].
- ↑ (ang.) Dongsheng Yu, Analiza wpływu sił Coriolisa na przepływ w estuarium rzeki Jangcy, referat na sympozjum w Uniwersytecie Cheng Kung, Tajwan.
- ↑ N.V. Makarova, V.I. Makarov, T.V. Sukhanova, Ratio between erosion and tectonic processes in platforms and mountainous regions, „Moscow University Geology Bulletin”, vol. 63, nr 5 (2008).
Bibliografia[edytuj | edytuj kod]
- B. Jaworski i in., Kurs fizyki, t. 1, Państwowe Wydawnictwo Naukowe, Warszawa 1971.
- Andrzej Januszajtis, Fizyka dla politechnik, PWN, Warszawa 1977.










