Siła Lorentza

Kierunek działania siły Lorentza w zależności od ładunku cząstki

Wiązka elektronów poruszających się po orbicie kołowej w stałym polu magnetycznym

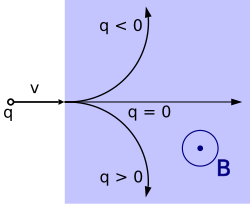
Siła Lorentza – siła, jaka działa na cząstkę obdarzoną ładunkiem elektrycznym, poruszającą się w polu elektromagnetycznym. Wzór podany został po raz pierwszy przez Hendrika Lorentza i dlatego nazwano go jego nazwiskiem.

Wzór określa, jak siła działająca na ładunek zależy od pola elektrycznego i pola magnetycznego (składników pola elektromagnetycznego):

$\mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),$

gdzie:

• $\mathbf {F}$ – wektor siły (w niutonach),
• $q$ – ładunek elektryczny cząstki (w kulombach),
• $\mathbf {E}$ – wektor natężenia pola elektrycznego (w woltach/metr),
• $\mathbf {B}$ – pseudowektor indukcji magnetycznej (w teslach),
• $\mathbf {v}$ – wektor prędkości cząstki (w metrach na sekundę),
• $\times$ – iloczyn wektorowy.

W przypadku, gdy terminem „siła Lorentza” określa się tylko samą składową magnetyczną tej siły, wzór na jej obliczanie zredukuje się do formuły następującej:

$\mathbf {F} =q(\mathbf {v} \times \mathbf {B} ).$

W ośrodkach ciągłych

Dla ośrodków ciągłych ładunek elektryczny wyraża się poprzez jego gęstość $\rho ,$ a natężenie prądu przez gęstość prądu $\mathbf {J} ,$ wówczas:

$\mathbf {F} =\int \limits _{V}(\rho \mathbf {E} +\mathbf {J} \times \mathbf {B} )dV.$

Składowa magnetyczna siły Lorentza dla przewodników z prądem nazywana jest siłą elektrodynamiczną.

Czterowektor siły Lorentza

Czterowektor siły Lorenzta w elektrodynamice klasycznej jest określony według wzoru:

$K^{\mu }=-qu_{\nu }F^{\mu \nu }=qu_{\nu }F^{\nu \mu },$

(1)

gdzie:

• $q$ ładunek cząstki, na którą działa pole elektromagnetyczne,
• $u_{\nu }=\eta _{\nu \mu }u^{\mu }$ jest to kowariantny czterowektor prędkości,
• $F^{\mu \nu }$ jest to tensor pola elektromagnetycznego,
• $\eta _{\mu \nu }$ jest to tensor metryczny Minkowskiego, przyjęliśmy tutaj sygnaturę tensora metrycznego Minkowskiego w postaci $(1,-1,-1,-1),$ bowiem przy sygnaturze przeciwnej, tzn.: $(-1,1,1,1),$ mamy wzór czterwektora siły w postaci:

$K^{\mu }=qu_{\nu }F^{\mu \nu }.$

(2)

Wykorzystując definicję tensora pola elektromagnetycznego można obliczyć część czasową i przestrzenną czterowektora siły w elektrodynamice klasycznej, zatem po wywodach mamy:

$K^{\mu }=\left({\frac {{\vec {p}}\cdot {\vec {F}}}{E}}\gamma ,{\frac {\gamma }{c}}{\vec {F}}\right),$

(3)

gdzie:

• ${\vec {F}}$ jest to wektor siły Lorentza,
• ${\vec {p}}$ jest to wektor pędu cząstki,
• $E$ jest to całkowita relatywistyczna energia cząstki,
• $\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$ jest to definicja współczynnika $\gamma ,$

gdzie:

• $v$ jest to szybkość cząstki,
• $c$ jest to prędkość fal elektromagnetycznych w szczególności światła.

Powyższa definicja czterowektora siły w elektrodynamice klasycznej jest zgodna (taka sama) w szczególnej teorii względności.

Siła Lorentza w szczególnej teorii względności

Zależność między siłą a pędem pozostaje prawdziwa również dla cząstek relatywistycznych:

$\mathbf {F} ={\frac {d\mathbf {p} }{dt}},$

$\mathbf {F} ={\frac {d\left(\gamma m\mathbf {v} \right)}{dt}}=m{\frac {d\left(\gamma \mathbf {v} \right)}{dt}}.$

Siłę Lorentza w szczególnej teorii względności opisuje zależność:

$\mathbf {F} =m{\frac {d\left(\gamma \mathbf {v} \right)}{dt}}=q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),$

gdzie:

$\gamma \equiv {\frac {1}{\sqrt {1-v^{2}/c^{2}}}}$

jest czynnikiem Lorentza, $v$ – prędkością cząstki, a $c$ to prędkość światła w próżni.

Praca siły

Szybkość zmiany energii (moc) wywołana ruchem cząstki w stałym polu wynosi:

${\frac {d\left(\gamma mc^{2}\right)}{dt}}=q\mathbf {E} \cdot \mathbf {v} .$

Oznacza to, że tylko pole elektryczne wykonuje pracę.

Ruch cząsteczki w polu o zmiennym natężeniu musi uwzględniać zjawisko powstawania pola elektrycznego w wyniku zmian pola magnetycznego i powstawania pola magnetycznego w wyniku zmian pola elektrycznego.

Zobacz też

• efekt Halla (klasyczny)
• trzecia siła

Bibliografia

• David J. Griffths, Podstawy elektrodynamiki, Wydawnictwo Naukowe PWN, Warszawa 2006.

Linki zewnętrzne

• Animacja siły Lorentza. bigs.de. [zarchiwizowane z tego adresu (2016-08-06)].