Wypukłość funkcji

Wypukłość i wklęsłość funkcji – własności funkcji mówiące o położeniu jej wykresu względem stycznej do niego w danym punkcie. Jeśli wykres znajduje się

• nad styczną – mówimy, że jest wypukła,
• pod styczną – mówimy, że jest wklęsła.

Definicja

Wypukłość

Funkcję rzeczywistą $f$ określoną na zbiorze wypukłym $C$ nazywamy wypukłą, jeżeli

$\forall _{x_{1},x_{2}\in C}\ \forall _{\alpha ,\beta \in [0,1],\,\alpha +\beta =1}\ f(\alpha x_{1}+\beta x_{2})\leqslant \alpha f(x_{1})+\beta f(x_{2}).$

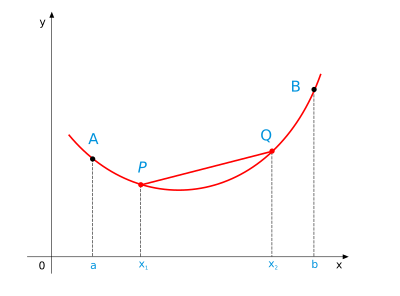
Jeśli $C$ jest przedziałem, to geometryczny sens powyższej nierówności jest następujący: łuk wykresu funkcji łączący dowolne dwa punkty $P,Q$ tego wykresu leży poniżej lub na cięciwie $PQ$.

Wklęsłość

Funkcję $f\colon C\to \mathbb {R}$ nazywamy wklęsłą w tym przedziale, jeżeli w powyższej definicji słowo poniżej zastąpimy przez powyżej, czyli innymi słowy zmienimy zwrot nierówności. Jeszcze inaczej: funkcja $f$ jest wklęsła, jeśli funkcja $-f$ jest wypukła.

Terminologia

Niewielka liczba autorów nazywa funkcje wypukłe w sensie powyższej definicji wklęsłymi i na odwrót; spotyka się też określenia wypukła w dół i wypukła w górę na funkcje wypukłą i wklęsłą odpowiednio.

Zastępując nierówności w definicji wypukłości (wklęsłości) przez nierówności ostre definiujemy funkcje ściśle wypukłe (ściśle wklęsłe)

Własności

Można pokazać, że funkcja wypukła – a zatem i wklęsła – na zbiorze otwartym jest ciągła. Założenie to jest istotne.

Funkcja wypukła jest kresem górnym rodziny funkcji liniowych mniejszych bądź równych od niej (punktowo).

Kryterium wypukłości funkcji ciągłych

Jeśli funkcja $f$ jest funkcją ciągłą określoną na przedziale $P\subset \mathbb {R}$ spełnia warunek

$\forall _{x,y\in P}\;f\left({\frac {x}{2}}+{\frac {y}{2}}\right)\leqslant {\frac {f(x)+f(y)}{2}}$

to funkcja jest wypukła na tym przedziale. Prawdziwa jest również implikacja odwrotna.

Funkcja różniczkowalna

Jeśli funkcja $f$ jest funkcją różniczkowalną określoną na przedziale otwartym, można podać równoważne definicje opierające się na pojęciu stycznej.

Wypukłość

Funkcja $f(x)$ jest wypukła w przedziale $(a,b)$ wtedy i tylko wtedy, gdy wykres funkcji leży ponad wykresem stycznej dla każdego punktu $x_{0}$ z przedziału $(a,b).$ W przypadku funkcji różniczkowalnej zapisuje się to wzorem

$\forall _{x,x_{0}\in (a,b)}\;f(x)-f(x_{0})\geqslant f'(x_{0})(x-x_{0}).$

Równanie stycznej do krzywej $y=f(x)$ w punkcie $x_{0}$ ma postać: $y=f(x_{0})+f'(x_{0})(x-x_{0}).$

Jeśli funkcja $f(x)$ jest dwukrotnie różniczkowalna na $(a,b),$ to aby była ona wypukła (wklęsła ku dołowi) w przedziale $(a,b),$ wystarczy żeby jej druga pochodna w tym przedziale była nieujemna: $\forall _{x\in (a,b)}\;f''(x)\geqslant 0.$

Wklęsłość

Funkcja $f(x)$ jest wklęsła w przedziale $(a,b)$ wtedy i tylko wtedy, gdy wykres funkcji leży pod wykresem stycznej dla każdego punktu $x_{0}$ z przedziału $(a,b).$ W przypadku funkcji różniczkowalnej zapisuje się to wzorem:

$\forall _{x,x_{0}\in (a,b)}\;f(x)-f(x_{0})\leqslant f'(x_{0})(x-x_{0}).$

Jeśli funkcja $f(x)$ jest dwukrotnie różniczkowalna na $(a,b),$ to aby była ona wklęsła (wypukła ku górze) (w przedziale $(a,b)$), wystarczy żeby druga pochodna w tym przedziale była niedodatnia: $\forall _{x\in (a,b)}f''(x)\leqslant 0.$

Punkt przegięcia

Jeżeli z jednej strony punktu $x_{0}$ funkcja jest wypukła zaś z drugiej wklęsła, to $x_{0}$ nazywamy punktem przegięcia krzywej.

O ile druga pochodna w punkcie $x_{0}$ istnieje, warunkiem koniecznym na to aby punkt $x_{0}$ był punktem przegięcia funkcji $f$ jest:

$f''(x_{0})=0.$

Nie jest to jednak warunek wystarczający, gdyż w punkcie $x_{0}$ musi nastąpić zmiana znaku drugiej pochodnej.

Przykład

Rozważmy funkcję rzeczywistą $f(x)=x^{4}.$ Jej druga pochodna $f''(x)=12x^{2}$ zeruje się jedynie w punkcie $x_{0}=0.$ W tym punkcie nie następuje jednak zmiana znaku drugiej pochodnej co oznacza, że funkcja $f$ nie ma punktów przegięcia. Ponadto druga pochodna jest nieujemna w całej dziedzinie, więc funkcja $f$ jest funkcją wypukłą w całej dziedzinie.

Zobacz też

• nierówność Jensena

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Convex Function, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2025-04-18].
• Convex function (of a real variable) (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2025-04-8].