Punkt przegięcia
| Niektóre z zamieszczonych tu informacji wymagają weryfikacji. Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu. |

Punkt przegięcia – niejednoznaczne pojęcie matematyczne, definiowane inaczej – i nierównoważnie – w analizie oraz geometrii. W obu dyscyplinach występują różne konwencje znaczeń:
- dla funkcji rzeczywistej o zmiennej rzeczywistej jest to pewien punkt w jej dziedzinie lub na wykresie. Zachodzi w nim zmiana wypukłości, tj. po jednej stronie przegięcia funkcja jest wypukła, a po drugiej – wklęsła[1][2]. Ta definicja jest niejednoznaczna przez różne użycie nazw „wypukłość” i „wklęsłość”; oprócz tego bywa zawężana dodatkowymi warunkami na zachowanie funkcji w tym miejscu. Przy niektórych z tych zawężeń – oraz innych definicjach, nieodwołujących się do wypukłości – punkt przegięcia wykresu staje się szczególnym przypadkiem sensu geometrycznego:
- dla ogólnych krzywych płaskich punkt przegięcia to taki, w którym istnieje styczna i „przechodzi” ona z jednej strony krzywej na drugą[3][4]. W sensie ścisłym i węższym[5]: w pewnym sąsiedztwie przegięcia krzywa zawiera się we wnętrzu kątów wierzchołkowych utworzonych przez styczną i normalną[6]. Można to też formalizować przez zmianę znaku krzywizny[7], choć wymaga to innych założeń o własnościach krzywej[potrzebny przypis].
Oprócz tego znaczenia z pierwszej grupy mają swoje warunki wystarczające jak:
- ekstremum pierwszej pochodnej we wnętrzu dziedziny[8],
- zmiana znaku drugiej pochodnej[9][10],
- zmiana znaku pewnych wyrażeń z pierwszą lub drugą pochodną w przegięciu,
- zerowanie się pochodnych kolejnych rzędów między pierwszym a pewnym rzędem nieparzystym, dla którego wartość pochodnej jest niezerowa[11][12]:
Kryteria te istnieją dzięki twierdzeniom o różniczkowalnych funkcjach wypukłych i wklęsłych. Przy pewnym zawężeniu pojęć te warunki wystarczające stają się równoważnymi; bywają wręcz używane jako definicje[11].
Pojęcie to wprowadził do matematyki prawdopodobnie Gilles de Roberval; posłużył się nim w 1636 roku, w liście do Pierre’a Fermata. O przegięciach pod innymi nazwami wspominali potem między innymi Gottfried Wilhelm Leibniz i Isaac Newton[13].
Przegięcia funkcji rzeczywistych[edytuj | edytuj kod]



Szeroka definicja przez wypukłość[edytuj | edytuj kod]
Niech będzie funkcją zmiennej rzeczywistej o wartościach rzeczywistych: gdzie Wtedy mówi się, że ma punkt przegięcia w wtedy i tylko wtedy, gdy w pewnym otoczeniu punktu jest po jednej z jego stron ściśle wypukła, a po drugiej – ściśle wklęsła[14]. Formalnie oznacza to, że istnieje liczba dla której funkcja
- a) jest ściśle wklęsła na przedziale i ściśle wypukła na przedziale
- b) odwrotnie – jest ona ściśle wypukła na i ściśle wklęsła na
Wypukłość i wklęsłość są definiowane różnie – i nierównoważnie – przez różnych autorów. W ogólności funkcja
- jest ściśle wklęsła na przedziale wtedy i tylko wtedy, gdy jest ciągła na przedziale i:
- lub (równoważna definicja[potrzebny przypis]):
- Podobnie funkcja jest ściśle wypukła na tym przedziale wtedy i tylko wtedy, gdy jest ciągła na tym przedziale i:
- lub (równoważna definicja):
Inne definicje[edytuj | edytuj kod]

Niektórzy matematycy definiują punkty przegięcia funkcji przez wypukłość i wklęsłość w sąsiedztwie, ale określone inaczej – za pomocą stycznych[1][15]. Wymaga to wzmocnienia założenia ciągłości o różniczkowalność[16]. Zdarza się też dodatkowy wymóg, by w tym sąsiedztwie przegięcia istniała także druga pochodna i to ciągła[17]; takie funkcje bywają nazywane klasą .
Nierzadko zakłada się też dodatkowe własności funkcji w samym punkcie jak:
- określoność w tym punkcie[14] (przyjmowanie w nim jakiejś wartości: );
- ciągłość[b]:
- istnienie w nim pochodnych jednostronnych spełniających pewne nierówności[2];
- istnienie w nim stycznej[18], czyli spełnianie jednego z dwóch warunków[19]:
- istnienie pochodnej właściwej lub niewłaściwej (tj. nieskończonej)[20]:
- istnienie jednostronnych pochodnych niewłaściwych:
- różniczkowalność[16] – istnienie pochodnej właściwej (tj. skończonej):
- istnienie drugiej pochodnej (podwójna różniczkowalność) i jej ciągłość[17][21]:
Czasem przegięcie funkcji jest definiowane bez wypukłości ani wklęsłości. Niektórzy odwołują się do własności związanych ze styczną w tym punkcie
- nieformalnie przegięcie to punkt przecinania stycznej[21]. To znaczenie obejmuje też funkcje bez zmiany wypukłości, w dodatku z wykresem po jednej stronie prostej normalnej – wbrew ogólnej definicji przegięcia krzywej płaskiej. Tak się może dziać w wypadku stycznych pionowych[5].
- Wykluczenie stycznych pionowych oznacza, że w przegięciu istnieje pochodna skończona Wtedy przebijanie stycznej to formalnie zmiana znaku funkcji gdzie to funkcja opisująca styczną w punkcie [c][20]. Ta definicja również bywa zawężana[d]. Wszystkie takie przegięcia są zgodne z definicją geometryczną (dla ogólnej krzywej płaskiej); mimo to mogą one nie zmieniać wypukłości funkcji, co opisano dalej.
Zdarza się jeszcze inna definicja – pozwalająca rozstrzygnąć, czy punkt jest przegięciem, za pomocą samych pochodnych w tym punkcie. Wymaga to co najmniej trzykrotnej różniczkowalności (istnienia )[11].
Przykłady nierównoważności[edytuj | edytuj kod]
Powyższe definicje nie są sobie równoważne – istnieją funkcje z punktami spełniającymi tylko niektóre z nich. Są przypadki zmiany wypukłości, w których[potrzebny przypis]:
- druga pochodna jest nieciągła;
- nie ma drugiej pochodnej – por. funkcja W punkcie istnieje przegięcie, bo pierwsza pochodna ma tam swoje minimum. Mimo to drugie pochodne jednostronne są tam różne więc obustronna druga pochodna nie istnieje;
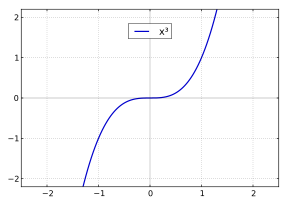
- nie ma pierwszej pochodnej właściwej (skończonej) – por. pierwiastek kubiczny (sześcienny);
- nie ma nawet niewłaściwej pierwszej pochodnej;
- nie ma stycznej[22];
- nie ma ciągłości;
- nie ma wartości w tym punkcie; por.
Istnieją też funkcje z punktami spełniającymi „geometryczną” definicję przegięcia (przez styczną), ale bez zmiany wypukłości w tym punkcie[20][2]:
Ta funkcja jest różniczkowalna w zerze ale jej pochodna jest tam nieciągła i nawet nie ma granic jednostronnych[23]. Warunek ciągłości pochodnej nie usuwa jednak takich przypadków. Nie robi tego nawet postulat dwukrotnej różniczkowalności z ciągłą drugą pochodną Istnieją funkcje tej klasy, które również przecinają swoją styczną bez zmiany wypukłości w tym punkcie[24]:
Warunki konieczne i wystarczające[edytuj | edytuj kod]


W przegięciach druga pochodna w ogólności nie musi istnieć, ale może przyjmować tylko zerową wartość [3][4]. Ten warunek konieczny nie jest jednak warunkiem wystarczającym:
- jeśli obie pochodne (pierwsza i druga) się zerują, to punkt może nie być przegięciem, lecz ekstremum[25] – por.
- jeśli druga pochodna się zeruje, a pierwsza nie, to punkt nie jest ekstremum, ale nie musi też być przegięciem; por. jedna z dalszych ilustracji.
Dla różnych klas funkcji można wskazać różne warunki wystarczające przegięcia:
- Jeśli funkcja ma obustronną pochodną w pewnym otoczeniu punktu wówczas warunkiem wystarczającym jest właściwe ekstremum lokalne pierwszej pochodnej w punkcie Ten warunek nie jest w ogólności konieczny – w sąsiedztwie przegięcia pochodna może w ogóle nie istnieć[26]. Mimo to, tak jak napisano wyżej, czasem zakłada się różniczkowalność badanej funkcji w całym przedziale – wprost lub przez definiowanie wypukłości za pomocą stycznych.
- Warunkiem wystarczającym istnienia punktu przegięcia jest też istnienie drugiej pochodnej funkcji równej zeru w punkcie oraz zmiana jej znaku w tym punkcie[4].
- Dla funkcji trzykrotnie różniczkowalnej warunkiem wystarczającym jest: W ogólności: jeśli w jakimś punkcie pierwsza nieznikająca (różna od zera) pochodna jest rzędu nieparzystego większego niż dwa, to jest tam przegięcie[27].
Rola przegięć[edytuj | edytuj kod]
Poszukiwanie przegięć to jeden z klasycznych elementów badania przebiegu zmienności funkcji rzeczywistych[14] Punkty te mogą się pojawić w analizie pochodnych, począwszy od pierwszej – mogą się znaleźć wśród punktów krytycznych badanej funkcji Przegięcia – tak jak lokalne ekstrema – mogą występować zarówno wśród:
- punktów nieróżniczkowalności (braku pochodnej)[14]; przy czym taki punkt może być jednocześnie i ekstremum, i przegięciem[22];
- punktów stacjonarnych, czyli miejsc zerowych pierwszej pochodnej Takie punkty stacjonarne bez ekstremum w przypadku jednowymiarowym mogą należeć do przegięć. Bywają nazywane punktami siodłowymi[28], przy czym te ostatnie są też definiowane inaczej – geometrycznie, jako punkty zerowej krzywizny[29]. Wtedy punkty siodłowe nie są szczególnym przypadkiem różniczkowalnych przegięć, lecz ich uogólnieniem na wiele wymiarów.
W ogólności przegięcie wykresu nie ma ścisłego związku z pierwszą pochodną. Jeśli w takich punktach ona istnieje, to może mieć dowolny znak i być nieskończona (niewłaściwa), co ilustrują wykresy obok. Przegięcia są bliżej związane z dalszymi pochodnymi – przez różne warunki konieczne lub wystarczające, opisane wyżej.
Przegięcia wielomianów[edytuj | edytuj kod]
Wielomian n-tego stopnia ma co najwyżej punktów przegięcia[potrzebny przypis]. Wynika to z połączenia trzech faktów:
- podwójna różniczkowalność wielomianów, dająca też ciągłą drugą pochodną (klasa ); przegięcia takich funkcji muszą spełniać warunek konieczny, jakim jest zerowanie się drugiej pochodnej
- wzór na pochodną wielomianu – dla pochodna zmniejsza stopień wielomianu o jeden. Przez to druga pochodna ma stopień niższy o dwa
- zasadnicze twierdzenie algebry mówi między innymi, że liczba pierwiastków rzeczywistych wielomianu rzeczywistego nie przekracza jego stopnia; tutaj liczba pierwiastków drugiej pochodnej nie przekracza
W szczególności funkcje kwadratowe – dla których – nie mają przegięć. Dotyczy to także wielomianów stopnia niższego niż dwa, czasem zwanych funkcjami liniowymi[potrzebny przypis].
Uogólnienie na inne krzywe płaskie[edytuj | edytuj kod]
Pojęcie punktu przegięcia może też zostać uogólnione na krzywe płaskie niebędące wykresami funkcji, zwłaszcza na krzywe z punktami regularnymi, tj. o unikalnej stycznej. Tak jak wspomniano, tutaj również występują różne konwencje:
- nieformalnie – w punkcie przegięcia krzywa przechodzi z jednej strony stycznej na drugą[30];
- w sensie ścisłym i węższym[5]: w pewnym sąsiedztwie przegięcia krzywa zawiera się we wnętrzu kątów wierzchołkowych utworzonych przez styczną i normalną[6];
- inna ścisła definicja mówi o rozdzielaniu punktów o krzywiźnie dodatniej i ujemnej[7], co wymaga zerowania się krzywizny w tym punkcie[31]. Tak rozumiane przegięcie jest szczególnym, jednowymiarowym przypadkiem punktu siodłowego lub – przy innych definicjach – jego odpowiednikiem.
W miarę zbliżania się do punktu przegięcia promień krzywizny wykresu funkcji dwukrotnie różniczkowalnej rośnie do nieskończoności. Mówi się skrótowo, że jest on w punkcie przegięcia nieskończony. Oznacza to, że w otoczeniu punktu przegięcia krzywa (w szczególności np. wykres funkcji) jest lepiej przybliżana linią prostą niż łukiem okręgu[potrzebny przypis].
Zobacz też[edytuj | edytuj kod]
Uwagi[edytuj | edytuj kod]
- ↑ W analizie czasem przyjmuje się, że przegięciem jest tu współrzędna odcięta tego punktu, czyli argument
- ↑ Taką definicję sugeruje Fichtenholz 1999 ↓, s. 264–266. Pisze wprost, że w punkcie przegięcia może nie być stycznej, co oznacza brak wymogu pochodnej, nawet niewłaściwej. Zarazem definiuje przegięcie jako punkt nie w dziedzinie, ale na krzywej, a krzywa bywa definiowana jako ciągły obraz przedziału liczbowego.
- ↑ to wielomian stopnia co najwyżej pierwszego, czasem zwany funkcją liniową.
- ↑ Różnica może być zapisana inaczej. Jeśli to:
- dla pewnego
Przypisy[edytuj | edytuj kod]
- ↑ a b Zaporożec 1967 ↓, s. 160.
- ↑ a b c d e Krych 2010 ↓, s. 171.
- ↑ a b punkt przegięcia, [w:] Encyklopedia PWN [dostęp 2022-01-16].
- ↑ a b c Żakowski 1972 ↓, s. 236.
- ↑ a b c d Fichtenholz 1999 ↓, s. 265.
- ↑ a b
 Point of inflection (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, 6 czerwca 2020 [dostęp 2022-01-16].
Point of inflection (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, 6 czerwca 2020 [dostęp 2022-01-16].
- ↑ a b Eric W. Weisstein, Inflection Point, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2022-01-16].
- ↑ Ryll i Skwarczyński 1995 ↓, s. 148.
- ↑
 Szymon Charzyński, Punkty przegięcia, kanał Khan Academy Po Polsku na YouTube, 5 maja 2014 [dostęp 2022-01-23].
Szymon Charzyński, Punkty przegięcia, kanał Khan Academy Po Polsku na YouTube, 5 maja 2014 [dostęp 2022-01-23].
- ↑ Wrzosek 2016 ↓, s. 148.
- ↑ a b c punkt, [w:] Encyklopedia PWN [dostęp 2022-01-27].
- ↑ Krych 2010 ↓, s. 220.
- ↑
 Jeff Miller i Siegmund Probst, Inflection point, [w:] Earliest Known Uses of Some of the Words of Mathematics (I) (ang.), MacTutor History of Mathematics archive, mathshistory.st-andrews.ac.uk [dostęp 2022-01-16].
Jeff Miller i Siegmund Probst, Inflection point, [w:] Earliest Known Uses of Some of the Words of Mathematics (I) (ang.), MacTutor History of Mathematics archive, mathshistory.st-andrews.ac.uk [dostęp 2022-01-16].
- ↑ a b c d e f
 Wypukłość. Badanie funkcji jednej zmiennej, [w:] Analiza matematyczna 1, wazniak.mimuw.edu.pl, 3 października 2021 [dostęp 2022-01-23].
Wypukłość. Badanie funkcji jednej zmiennej, [w:] Analiza matematyczna 1, wazniak.mimuw.edu.pl, 3 października 2021 [dostęp 2022-01-23].
- ↑ Wrona 1965 ↓, s. 356.
- ↑ a b Leksiński, Nabiałek i Żakowski 1995 ↓, s. 94.
- ↑ a b Leksińska i Leksiński 1978 ↓, s. 150.
- ↑
 Jeff Miller, Ambiguously Defined Mathematical Terms at the High School Level (ang.), 30 września 2018, zarchiwizowane z adresu [dostęp 2022-01-26].
Jeff Miller, Ambiguously Defined Mathematical Terms at the High School Level (ang.), 30 września 2018, zarchiwizowane z adresu [dostęp 2022-01-26].
- ↑ Fichtenholz 1999 ↓, s. 181.
- ↑ a b c Strzelecki 2018 ↓, s. 142.
- ↑ a b c Krysicki i Włodarski 1994 ↓, s. 187.
- ↑ a b Krych 2010 ↓, s. 172.
- ↑ Strzelecki 2018 ↓, s. 129.
- ↑ Fichtenholz 1999 ↓, s. 266.
- ↑ pochodna funkcji, [w:] Encyklopedia PWN [dostęp 2022-01-16].
- ↑ Banach 1957 ↓, s. 177.
- ↑ Królikowski i Steckiewicz 1964 ↓, s. 214.
- ↑ Eric W. Weisstein, Saddle Point, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2022-01-17].
- ↑ powierzchnia minimalna, [w:] Encyklopedia PWN [dostęp 2022-01-23].
- ↑ Punkt przegięcia, [w:] Encyklopedia Popularna PWN, Państwowe Wydawnictwo Naukowe, Warszawa 1986, ISBN 83-01-01-750-3, s. 641.
- ↑ Krysicki i Włodarski 2006 ↓, s. 95.
Bibliografia[edytuj | edytuj kod]
- Książki publikowane drukiem
- Stefan Banach: Rachunek różniczkowy i całkowy. Wyd. VI. Warszawa: Państwowe Wydawnictwo Naukowe, 1957.
- G.M. Fichtenholz: Rachunek różniczkowy i całkowy. Wyd. 12. T. 1. Warszawa: Wydawnictwo Naukowe PWN, 1999. ISBN 83-01-02175-6.
- Jerzy Królikowski, Celestyn Steckiewicz: Matematyka. Wzory, definicje i tablice. Wyd. VIII poprawione. Warszawa: Wydawnictwa Komunikacji i Łączności, 1964.
- Michał Krych: Analiza matematyczna dla ekonomistów. Wyd. I. Warszawa: Wydawnictwa Uniwersytetu Warszawskiego, 2010. ISBN 978-83-235-0776-5.
- Włodzimierz Krysicki, Lech Włodarski: Analiza matematyczna w zadaniach. Wyd. XXI. T. 1. Warszawa: Wydawnictwo Naukowe PWN, 1994. ISBN 83-01-01460-1.
- Włodzimierz Krysicki, Lech Włodarski: Analiza matematyczna w zadaniach. Wyd. 27. T. 2. Warszawa: Wydawnictwo Naukowe PWN, 2006. ISBN 978-83-01-14296-4.
- Franciszek Leja: Rachunek różniczkowy i całkowy ze wstępem do równań różniczkowych. Wyd. VI. Warszawa: Państwowe Wydawnictwo Naukowe, 1963, seria: Biblioteka Matematyczna, tom 2.
- Anna Leksińska, Wacław Leksiński: Elementy matematyki wyższej dla studentów i kandydatów na studia. Warszawa: Państwowe Wydawnictwo Naukowe, 1978, seria: Matematyka dla politechnik.
- Wacław Leksiński, Ireneusz Nabiałek, Wojciech Żakowski: Matematyka. Definicje, twierdzenia, przykłady, zadania. Wyd. V. Warszawa: Wydawnictwa Naukowo-Techniczne, 1995, seria: Podręczniki akademickie: elektronika, informatyka, telekomunikacja. ISBN 83-204-1892-5.
- Jerzy Ryll, Maciej Skwarczyński: Działania nieskończone [w:] Leksykon matematyczny. Warszawa: Wydawnictwo „Wiedza Powszechna”, 1995. ISBN 83-214-0783-8.
- Włodzimierz Wrona: Matematyka. Podstawowy wykład politechniczny, część I. Wyd. II poprawione. Warszawa: Państwowe Wydawnictwo Naukowe, 1965.
- Dariusz Wrzosek: Matematyka dla biologów. Wyd. II, zmienione. Warszawa: Wydawnictwa Uniwersytetu Warszawskiego, 2016. ISBN 978-83-235-0460-3.
- G.I. Zaporożec: Metody rozwiązywania zadań z analizy matematycznej. Piotr Kucharczyk (tłum.). Wyd. I. Warszawa: Wydawnictwa Naukowo-Techniczne, 1967.
- Wojciech Żakowski: punkt przegięcia, [w:] Mały słownik matematyczny. Warszawa: Wydawnictwo „Wiedza Powszechna”, 1972.
- Dokumenty cyfrowe
- Paweł Strzelecki, Analiza matematyczna I (skrypt wykładu) [online], 14 grudnia 2018 [dostęp 2022-01-27].
Linki zewnętrzne[edytuj | edytuj kod]
 Mariusz Śliwiński, Wklęsłość i wypukłość krzywej, math.edu.pl [dostęp 2022-07-02].
Mariusz Śliwiński, Wklęsłość i wypukłość krzywej, math.edu.pl [dostęp 2022-07-02].








![{\displaystyle y\!=\!{\sqrt[{3}]{x}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/622057ee961ff8fa44795cd2dace54ef6bb5b9bc)

















![{\displaystyle [u,v]\subseteq X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5066407eae68122b742832cb9bbc9c7a3d3b012)

























































