Przesunięcie ku czerwieni

Przesunięcie ku czerwieni, poczerwienienie, redshift – zjawisko fizyczne polegające na tym, że linie widmowe promieniowania elektromagnetycznego docierające z niektórych gwiazd lub galaktyk są przesunięte w stronę większych długości fali (mniejszych częstotliwości)[1] .
Z definicji przesunięcie ku czerwieni jest pomniejszonym o jeden stosunkiem długości fali odebranej z ciała niebieskiego do długości fali emitowanej. Jeżeli emitowana fala ma długość a obserwuje się falę o długości to związek pomiędzy tymi długościami można wyrazić wzorem
gdzie jest przesunięciem ku czerwieni.
Określenie przesunięcia ku czerwieni wprowadzono ze względu na fakt, iż światło widzialne o najdłuższej fali ma kolor czerwony i w kierunku tego krańca widma przesuwają się linie. Zamiennie mówi się też o poczerwienieniu światła lub widma gwiazdy. Pojęcie to jest na tyle zakorzenione w astronomii, iż również dla zakresu długofalowego widma (podczerwieni czy wręcz fal radiowych) mówi się o przesunięciu ku czerwieni, choć tak naprawdę linie widmowe w tych pasmach oddalają się od barwy czerwonej.
W kosmologii efekt poczerwienienia obserwowany jest dla źródeł światła leżących w znacznej odległości od Ziemi (odległych galaktyk). Przesunięcie to jest proporcjonalne do odległości danego obiektu od Ziemi i jest podstawowym argumentem za modelem rozszerzającego się wszechświata (prawo Hubble’a-Lemaître’a).
Przesunięcie ku czerwieni wykrywa się, analizując położenie linii widmowych pochodzących z danego obiektu. Analizy dokonuje się poprzez porównanie spektroskopowe światła gwiazdy i linii widmowych pierwiastków w laboratorium (np. wodoru).
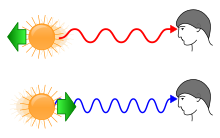

Przesunięcie ku czerwieni jest wywołane kilkoma przyczynami:
- Oddalanie się źródła światła. Podobne zjawisko zachodzi dla fal dźwiękowych i jest nazywane efektem Dopplera. W tym przypadku, ponieważ mamy do czynienia ze światłem, jest to relatywistyczny efekt Dopplera.
- Rozszerzanie się wszechświata. Poczerwienienie występuje w widmach odległych galaktyk jako konsekwencja ekspansji wszechświata – odleglejsze galaktyki mają większe przesunięcie ku czerwieni.
- Grawitacja – światło „pokonując” grawitację traci energię, czyli zwiększa długość fali. Przykładem jest efekt Sachsa-Wolfe’a. Grawitacyjne przesunięcie ku czerwieni występuje także w płaskiej czasoprzestrzeni, czyli przy braku grawitacji. We wszechświecie statycznym Einsteina natomiast czasoprzestrzeń jest zakrzywiona, ale nie występuje grawitacyjne przesunięcie ku czerwieni[3].
Analogicznie, przesunięcie ku fioletowi występuje, gdy obserwowane źródło światła zbliża się do obserwatora. Takie widma obserwuje się dla obiektów poruszających się w stronę Ziemi (np. Galaktyka Andromedy). Pole grawitacyjne również bywa powodem przesunięcia ku fioletowi[3].
Historia[edytuj | edytuj kod]
Historia odkrycia ma swój początek w XIX wieku i jest powiązana z efektem Dopplera. Christian Doppler wyjaśnił to zjawisko po raz pierwszy w roku 1842[4], a jego hipoteza została potwierdzona przez holenderskiego naukowca Christophorusa Buys-Ballot w 1845[5]. Doppler prawidłowo przewidział, iż ten fenomen można stosować w przypadku każdego rodzaju fal, ponadto zasugerował, że zróżnicowanie koloru gwiazd może być wynikiem ich ruchu względem Ziemi[6]. Zanim to zweryfikowano, odkryto iż kolory gwiazd miały związek z ich temperaturą, a nie ruchem.
Pierwsze przesunięcie ku czerwieni Dopplera zostało opisane przez francuskiego fizyka Armanda Fizeau w 1848 – wskazał on przesunięcie w liniach spektralnych gwiazd. Czasami efekt jest nazywany „efektem Dopplera-Fizeau”. W 1868 brytyjski astronom William Huggins jako pierwszy oszacował prędkość gwiazdy oddalającej się od Ziemi, używając wspomnianej metody[7].
W 1871 optyczne przesunięcie ku czerwieni potwierdzono, gdy zaobserwowano je w liniach Fraunhofera[8]. W 1887 Hermann Vogel i Julius Scheiner odkryli tzw. roczny efekt Dopplera – coroczną zmianę w przesunięciu Dopplera gwiazd, znajdujących się w pobliżu ekliptyki, spowodowane prędkością orbitalną Ziemi[9]. W 1901 Aristarch Biełopolski zweryfikował optyczne przesunięcie ku czerwieni za pomocą systemu rotujących luster[10].
Określenia „przesunięcie ku czerwieni” najwcześniej użył prawdopodobnie amerykański astronom Walter Sydney Adams w roku 1908, gdy wspomniał on o „dwóch metodach badania natury przesunięcia ku czerwieni”[11].
Wraz z obserwacjami, które rozpoczęto w 1912, Vesto Slipher odkrył, że większość galaktyk spiralnych, które wówczas uważano za mgławice spiralne, miała znaczące przesunięcia ku czerwieni[12]. Trzy lata później jego artykuł pojawił się w czasopiśmie „Popular Astronomy”[13]. W artykule stwierdził, iż znane wcześniej metody mogły służyć nie tylko do badań spektrum galaktyk, lecz również ich prędkości[14]. Slipher odnotował prędkości 15 mgławic, natomiast wszystkie – oprócz trzech – miały tzw. „prędkość dodatnią”. Następnie Edwin Hubble wykazał przewidzianą w 1927 roku przez Georges Lemaître zależność pomiędzy przesunięciami ku czerwieni tych „mgławic” oraz dystansem do nich, formułując prawo nazwane prawem Hubble’a-Lemaître’a[15]. Te obserwacje potwierdziły prace Aleksandra Friedmana z roku 1922, kiedy opracował on słynne równania Friedmana[16]. Obecnie są one uznawane jako mocny dowód na rozszerzanie się Wszechświata oraz na potwierdzenie teorii Wielkiego Wybuchu.
Pomiar oraz interpretacja[edytuj | edytuj kod]
Zmierzenie spektrum światła pochodzącego z jednego źródła (por. ilustrację na początku artykułu) jest możliwe. Aby określić przesunięcie ku czerwieni, poszukuje się takich elementów widma, jak linie absorpcyjne, linie emisyjne lub inne zmiany natężenia światła. Jeśli te parametry zostaną znalezione, można je porównać ze znanymi cechami w spektrum różnych związków chemicznych poprzez eksperymentowanie na związkach występujących na Ziemi. Bardzo powszechnym pierwiastkiem w kosmosie jest wodór. Spektrum pierwotnie pozbawionego cech światła padającego przez wodór pokaże sygnatury widmowe charakterystyczne dla wodoru, który wykazuje pewne cechy w regularnych odstępach czasu. Gdyby analizę ograniczyć tylko do linii absorpcyjnych, widmo wyglądałoby podobnie jak na ilustracji (u góry po prawej). Jeśli ten sam schemat występowania interwałów jest obecny w obserwowanym widmie z odległego źródła (lecz występuje przy przesuniętych długościach fal), wówczas także można zidentyfikować obecność tego pierwiastka. Jeśli ta sama linia widmowa zostanie zidentyfikowana w obu widmach – ale przy różnych długościach fal – wówczas można obliczyć przesunięcie ku czerwieni (zob. tabelę poniżej). Do określenia przesunięcia ku czerwieni obiektu tą metodą wymagana jest wartość częstotliwości lub zakresu długości fali.
Aby obliczyć przesunięcie ku czerwieni, potrzebna jest wartość długości fali taka, jaka zostałaby zmierzona przez obserwatora znajdującego się w sąsiedztwie źródła i poruszającego się wraz z nim. Ponieważ takiego pomiaru nie można wykonać bezpośrednio (wymagałoby to podróży do odległej gwiazdy będącej obiektem badań), stosuje się metodę wykorzystującą opisane linie widmowe. Przesunięć ku czerwieni nie można obliczyć w następujących przypadkach:
- poprzez obserwacje niezidentyfikowanych cech, których częstotliwość spoczynkowa jest nieznana,
- gdy rozważane widmo nie posiada żadnych cech,
- gdy występuje tzw. Szum biały (przypadkowe fluktuacje w widmie)[17].
Przesunięcie ku czerwieni (i przesunięcie ku fioletowi) można opisać jako względną różnicę między obserwowanymi a emitowanymi długościami (lub częstotliwościami) fal, emitowanych przez obiekt. W astronomii odwołanie do tej zmiany wykonuje się umownie za pomocą tzw. wielkości bezwymiarowej oznaczanej literą z. Jeśli λ reprezentuje długość fali, a f reprezentuje częstotliwość (należy zaznaczyć, że gdzie jest prędkością światła), wówczas z jest określone poniższymi równaniami[18]:
| Na podstawie długości fali | Na podstawie częstotliwości fali |
|---|---|
Po zmierzeniu wartości z, rozróżnienie między przesunięciem ku czerwieni a przesunięciem ku fioletowi jest po prostu kwestią tego, czy z jest dodatnie czy ujemne. Na przykład Dopplerowskie przesunięcia ku fioletowi są związane z obiektami poruszającymi się w stronę obserwatora (zbliżającymi się do niego). Analogicznie, Dopplerowskie przesunięcia ku czerwieni są związane z obiektami oddalającymi się od obserwatora. Podobnie, grawitacyjne przesunięcia ku fioletowi są związane ze światłem emitowanym ze źródła znajdującego się w słabszym polu grawitacyjnym, obserwowanym z silniejszego pola grawitacyjnego, podczas gdy grawitacyjne przesunięcie ku czerwieni implikuje przeciwne warunki.
Wzory[edytuj | edytuj kod]
Dla poszczególnych przestrzeni można wyprowadzić różne wzory na przesunięcie ku czerwieni, jak przedstawiono w poniższej tabeli. W każdym z przypadków, wielkość przesunięcia (wartość ) jest niezależna od długości fali.
Oznaczenia:
- – przesunięcie ku czerwieni,
- – prędkość (jeżeli obiekt oddala się od obserwatora, wartość jest dodatnia),
- – prędkość światła w próżni,
- – czynnik Lorentza,
- – czynnik skali,
- – stała grawitacji,
- – masa obiektu,
- – współrzędne Schwarzschilda,
- – komponenty tensoru metrycznego.
| Rodzaj przesunięcia | Przestrzeń | Wzór |
|---|---|---|
| Relatywistyczny efekt Dopplera | czasoprzestrzeń Minkowskiego (płaska czasoprzestrzeń) |
dla małych wartości dla ruchu, który odbywa się dokładnie w kierunku promieniowania |
| Kosmologiczne przesunięcie ku czerwieni |
czasoprzestrzeń FLRW (rozszerzający się wszechświat) |
|
| Grawitacyjne przesunięcie ku czerwieni |
dowolna stacjonarna czasoprzestrzeń (np. metryka Schwarzschilda) |
(dla metryki Schwarzschilda, ) |
Efekt Dopplera[edytuj | edytuj kod]
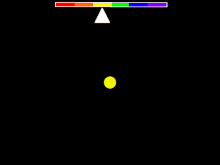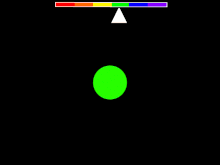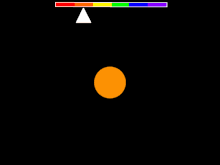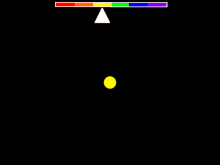
Jeżeli źródło światła oddala się od obserwatora, wówczas następuje przesunięcie ku czerwieni jeśli źródło zbliża się od obserwatora, wówczas następuje przesunięcie ku fioletowi Zależność ta występuje dla każdego rodzaju fal elektromagnetycznych, a jej naturę wyjaśnia efekt Dopplera. Tym samym, taki typ przesunięcia ku czerwieni jest nazywany dopplerowskim przesunięciem ku czerwieni. Jeżeli źródło oddala się od obserwatora z prędkością która jest dużo mniejsza od prędkości światła w próżni wówczas przesunięcie ku czerwieni wynosi:
- (gdy ),
gdzie jest prędkością światła w próżni. W klasycznym przypadku efektu Dopplera, częstotliwość źródła nie ulega zmianie, lecz ruch recesyjny powoduje złudzenie niższej częstotliwości.
Pełniejsza analiza dopplerowskiego przesunięcia ku czerwieni wymaga rozważenia efektów relatywistycznych, związanych z ruchem źródeł z prędkościami zbliżonymi do prędkości światła w próżni (w artykule relatywistyczny efekt Dopplera znajdują się kompleksowe obliczenia związane z tym efektem). W ogólnym ujęciu, obiekty poruszające się z prędkościami zbliżonymi do prędkości światła w próżni będą „doświadczać” odchyleń od powyższego wzoru ze względu na dylatację czasu opisaną w szczególnej teorii względności; można dokonać jej korekty, wprowadzając do klasycznego wzoru Dopplera czynnik Lorentza w następujący sposób (wyłącznie dla ruchu wzdłuż linii wzroku):
To zjawisko zaobserwowano po raz pierwszy podczas eksperymentu, przeprowadzonego w roku 1938 przez Herberta E. Ivesa oraz G.R. Stilwella – było to tzw. doświadczenie Ivesa-Stillwella[19].
Ponieważ czynnik Lorentza jest zależny tylko od wartości prędkości, przesunięcie ku czerwieni (powiązane z relatywistyczną korektą) będzie niezależne od kierunku poruszania się źródła. Dla porównania, główna część wzoru jest zależna od projekcji wektora ruchu źródła w kierunku pola widzenia, co daje różne wyniki dla różnych kierunków. Jeżeli jest kątem między kierunkiem ruchu względnego a kierunkiem emisji światła w stronę obserwatora[20] (kąt zerowy oznacza, iż źródło porusza się dokładnie w kierunku obserwatora), wzór opisujący relatywistyczny efekt Dopplera wygląda następująco:
natomiast dla ruchu wyłącznie wzdłuż linii wzroku równanie można uprościć do postaci:
Dla szczególnych przypadków, w których światło dociera do obserwatora pod kątem prostym do kierunku ruchu obiektu (z punktu widzenia obserwatora)[21], mówimy wówczas o poprzecznym przesunięciu ku czerwieni, a jego wartość wynosi:
Przesunięcie ku czerwieni następuje pomimo faktu, iż obiekt nie oddala się od obserwatora. Nawet gdy źródło porusza się w jego kierunku oraz występuje składowa poprzeczna względem ruchu, wówczas istnieje taka prędkość przy której dochodzi do niwelowania spodziewanego efektu przesunięcia ku fioletowi, natomiast przy prędkościach większych od nastąpi przesunięcie ku czerwieni źródła[22].
Rozszerzanie się Wszechświata[edytuj | edytuj kod]
Matematyczne pochodne[edytuj | edytuj kod]
Następstwa obserwacyjne rozszerzania się Wszechświata można uzyskać, stosując równania z ogólnej teorii względności, które opisują zasadę kosmologiczną jednorodnego i izotropowego Wszechświata.
Do wyznaczania efektu przesunięcia ku czerwieni używa się równania linii geodezyjnej dla fali świetlnej:
gdzie:
- – interwał czasoprzestrzeni,
- – interwał czasu,
- – interwał przestrzeni,
- – prędkość światła w próżni,
- – zależny od czasu kosmiczny czynnik skali,
- – zakrzywienie na jednostkę powierzchni.
Dla obserwatora obserwującego grzbiet fali świetlnej w pozycji i czasie grzbiet fali świetlnej jest emitowany w czasie w przeszłości oraz w odległej pozycji Całkując po czasie i przestrzeni, w której podróżuje fala świetlna, uzyskujemy równanie (oznaczone jako równanie nr 1):
Generalnie, długość fali światła jest różna dla dwóch innych pozycji i czasów, rozpatrywanych ze względu na zmieniające się właściwości metryki. Gdy fala zostanie wyemitowana, ma długość Następny grzbiet fali świetlnej jest emitowany w czasie:
Obserwator dostrzega następny grzbiet obserwowanej fali świetlnej o długości który przybywa w czasie
Ponieważ kolejny grzbiet fali jest ponownie emitowany z i jest obserwowany w zostaje utworzone równanie nr 2:
Prawe strony równań nr 1 oraz 2 są identyczne, co oznacza:
Wykonując poniższe przekształcenia
obliczamy, że
Dla bardzo małych zmian w czasie (w ciągu okresu jednego cyklu fali świetlnej) współczynnik skali jest w zasadzie stałą dzisiaj oraz ówcześnie. Dzięki temu uzyskujemy:
co można przekształcić następująco:
Korzystając z definicji przesunięcia ku czerwieni, przedstawionej powyżej, uzyskujemy następujące równanie:
W rozszerzającym się Wszechświecie, takim jak nasz, współczynnik skali jest funkcją monotonicznie rosnącą, a zatem jest dodatnie i zauważamy przesunięcie ku czerwieni w przypadku odległych galaktyk.
Rozróżnianie efektów kosmologicznych i lokalnych[edytuj | edytuj kod]
W przypadku kosmologicznych przesunięć ku czerwieni dodatkowe przesunięcia ku czerwieni Dopplera i przesunięcia w błękicie spowodowane osobliwymi ruchami galaktyk względem siebie powodują znaczne odchylenie względem standardowego prawa Hubble’a-Lemaître’a[23]. Wynikającą z tego sytuację można zilustrować rozszerzającym się „wszechświatem gumowym”, powszechną analogią kosmologiczną używaną do opisu rozszerzania się przestrzeni. Jeśli dwa obiekty są reprezentowane np. przez kulki z łożysk, a czasoprzestrzeń przez rozciągający się arkusz gumy, efekt Dopplera jest wywoływany przez toczenie kulek po arkuszu w celu wywołania szczególnego ruchu. Kosmologiczne przesunięcie ku czerwieni występuje, gdy wspomniane kulki są przyklejone do arkusza, a sam arkusz jest rozciągany[24][25][26].
Przesunięcia ku czerwieni galaktyk obejmują zarówno składową związaną z prędkością recesyjną wynikającą z ekspansji Wszechświata, jak i składową związaną ze szczególnym ruchem (przesunięcie Dopplera)[27].
Przesunięcie ku czerwieni spowodowane rozszerzaniem się wszechświata zależy od prędkości recesji w sposób określony przez model kosmologiczny wybrany do opisu rozszerzania się Wszechświata, który bardzo się różni od tego, jak przesunięcie ku czerwieni Dopplera zależy od prędkości lokalnej[28]. Opisując kosmologiczną ekspansję pochodzenia przesunięcia ku czerwieni, kosmolog Edward Robert Harrison powiedział: „Światło opuszcza galaktykę, która pozostaje w spoczynku w swoim lokalnym regionie przestrzeni i ostatecznie jest dostrzegane przez obserwatorów, którzy pozostają w spoczynku w swoim lokalnym regionie przestrzeni. Między galaktyką i obserwatorami, światło przemieszcza się przez rozległe obszary rozszerzającej się przestrzeni. W rezultacie wszystkie długości fal światła są rozciągane przez ekspansję przestrzeni. To takie proste…”[29]Steven Weinberg wyjaśnił: „Wzrost długości fali od emisji do absorpcji światła nie zależy od szybkości zmiany (w tym przypadku jest współczynnikiem skali Robertsona-Walkera) w czasie emisji lub absorpcji, ale zależy od wzrostu w całym okresie od emisji do absorpcji”[30].
W literaturze popularnej często używa się wyrażenia „Dopplerowskie przesunięcie ku czerwieni” zamiast „kosmologicznego przesunięcia ku czerwieni”, aby opisać przesunięcie ku czerwieni galaktyk zdominowanych przez ekspansję czasoprzestrzeni, ale kosmologicznego przesunięcia ku czerwieni nie stwierdza się za pomocą relatywistycznego równania Dopplera[31].
który zamiast tego charakteryzuje się szczególną teorią względności; zatem jest niemożliwe, podczas gdy ta zależność jest możliwa dla kosmologicznych przesunięć ku czerwieni, ponieważ przestrzeń między dwoma obiektami (takimi jak np. kwazar i Ziemia) może rozszerzać się szybciej niż prędkość światła[32]. W bardziej matematycznym znaczeniu, punkt widzenia, wg którego „odległe galaktyki oddalają się” i punkt widzenia, że „przestrzeń między galaktykami się rozszerza” są powiązane przez zmieniające się układy współrzędnych. Dokładne wyrażenie tej zależności wymaga zastosowania metryki Friedmana-Lemaître’a-Robertsona-Walkera.[33]
Gdyby Wszechświat kurczył się zamiast rozszerzać, widzielibyśmy odległe galaktyki z efektem przesunięcia ku fioletowi o wielkość proporcjonalną do ich odległości zamiast przesunięcia ku czerwieni[34].
Zobacz też[edytuj | edytuj kod]
Przypisy[edytuj | edytuj kod]
- ↑ przesunięcie ku czerwieni, [w:] Encyklopedia PWN [dostęp 2023-01-10].
- ↑ Uwaga: Ciało o dużej masie jest z lewej strony, masę ciała z prawej strony pominięto.
- ↑ a b Andrzej Okolow, Does time always slow down as gravity increases?, „arXiv”, 22 czerwca 2019, arXiv:1906.09405v1 [dostęp 2019-06-25] (ang.).
- ↑ Doppler, Christian: Beiträge zur fixsternenkunde. T. 69. Prague: G. Haase Söhne, 1846.
- ↑ Doppler Sonography: A Brief History. W: Maulik, Dev: Doppler Ultrasound in Obstetrics And Gynecology. 2005. ISBN 978-3-540-23088-5.
- ↑ O’Connor, John J, Robertson, Edmund F: Christian Andreas Doppler. University of St Andrews, 1998.
- ↑ Huggins, William. Further Observations on the Spectra of Some of the Stars and Nebulae, with an Attempt to Determine Therefrom Whether These Bodies are Moving towards or from the Earth, Also Observations on the Spectra of the Sun and of Comet II. „Philosophical Transactions of the Royal Society of London”. 158, s. 529–564, 1868.
- ↑ Reber, G. Intergalactic Plasma. „Astrophysics and Space Science”. 227, s. 93–96, 1995.
- ↑ A. Pannekoek: A History of Astronomy. Dover, 1961, s. 451. ISBN 0-486-65994-1.
- ↑ Bélopolsky, A. On an Apparatus for the Laboratory Demonstration of the Doppler-Fizeau Principle. „Astrophysical Journal”, s. 15, 1901.
- ↑ Adams, Walter S. Preliminary catalogue of lines affected in sun-spots. „Contributions from the Mount Wilson Observatory / Carnegie Institution of Washington”, s. 1–21, 1908. Carnegie Institution of Washington.
- ↑ Slipher, Vesto. The radial velocity of the Andromeda Nebula. „Lowell Observatory Bulletin”, s. 2.56–2.57, 1912.
- ↑ Slipher, Vesto. Spectrographic Observations of Nebulae. „Popular Astronomy”, s. 21–24, 1915.
- ↑ Slipher, Vesto. Spectrographic Observations of Nebulae. „Popular Astronomy”, s. 22, 1915.
- ↑ Hubble, Edwin. A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae. „Proceedings of the National Academy of Sciences of the United States of America”, s. 168–173, 1929.
- ↑ Friedman, A.A. Über die Krümmung des Raumes. „Zeitschrift für Physik”, s. 377–386, 1922.
- ↑ Zob. konferencję NASA z 25.05.2004 odnośnie do statelity Swift poszukującego rozbłysków gamma: „Pomiary widm promieniowania gamma uzyskane podczas głównego rozbłysku GRB okazały się mało wartościowe jako wskaźniki przesunięcia ku czerwieni ze względu na brak dobrze zdefiniowanych cech. Jednak w rezultacie obserwacji optycznych poświat rozbłysków otrzymano widma z możliwymi do zidentyfikowania liniami, co prowadzi do precyzyjnych pomiarów przesunięcia ku czerwieni”.
- ↑ W celu informacji nt. definiowania oraz interpretowania dużych wartości przesunięć ku czerwieni, zob. Extragalactic Redshifts.
- ↑ H. Ives, G. Stilwell. An Experimental study of the rate of a moving atomic clock. „J. Opt. Soc. Am.”. 28 (7), s. 215–226, 1938. DOI: 10.1364/josa.28.000215.
- ↑ Jurgen Freund: Special Relativity for Beginners. World Scientific, 2008, s. 120. ISBN 981-277-160-3.
- ↑ R. Ditchburn: Light. Dover, 1961, s. 329. ISBN 0-12-218101-8.
- ↑ Zob. „Photons, Relativity, Doppler shift”, University of Queensland.
- ↑ Pomiary szczególnych prędkości do 5 Mpc przy użyciu Kosmicznego Teleskopu Hubble’a zostały opisane w 2003 r. przez Karachentsev, i inni. Local galaxy flows within 5 Mpc. „Astronomy and Astrophysics”. 398 (2), s. 479–491, 2003. DOI: 10.1051/0004-6361:20021566. arXiv:astro-ph/0211011. Bibcode: 2003A&A...398..479K.
- ↑ Theo Koupelis, Karl F. Kuhn: In Quest of the Universe. Wyd. 5th. Jones & Bartlett wydawcas, 2007. ISBN 978-0-7637-4387-1.
- ↑ „Zupełnie słuszne jest interpretowanie równań względności w kategoriach rozszerzającej się przestrzeni. Błędem jest przesuwanie analogii zbyt daleko i nasycanie przestrzeni właściwościami fizycznymi, które nie są zgodne z równaniami względności” Geraint F. Lewis, Matthew J. Francis, Luke A. Barnes, Juliana Kwan i inni. Cosmological Radar Ranging in an Expanding Universe. „Monthly Notices of the Royal Astronomical Society”. 388 (3), s. 960–964, 2008. DOI: 10.1111/j.1365-2966.2008.13477.x. arXiv:0805.2197. Bibcode: 2008MNRAS.388..960L.
- ↑ Michal Chodorowski. Is space really expanding? A counterexample. „Concepts Phys”. 4 (1), s. 17–34, 2007. DOI: 10.2478/v10005-007-0002-2. arXiv:astro-ph/0601171. Bibcode: 2007ONCP....4...15C.
- ↑ Bedran,M.L. (2002)„A comparison between the Doppler and cosmological redshifts” Am.J.Phys. 70, s. 406–408.
- ↑ Edward Harrison. The redshift-distance and velocity-distance laws. „Astrophysical czasopismo, Part 1”. 403, s. 28–31, 1992. DOI: 10.1086/172179. Bibcode: 1993ApJ...403...28H. A pdf file can be found here [1].
- ↑ Edward Robert Harrison: Cosmology: The Science of the Universe. Wyd. 2nd. Cambridge University Press, 2000, s. 315. ISBN 978-0-521-66148-5.
- ↑ Steven Weinberg: Cosmology. Oxford University Press, 2008, s. 11. ISBN 978-0-19-852682-7.
- ↑ Odenwald & Fienberg 1993.
- ↑ „Dopuszcza się” istnienie prędkości większej niż prędkość światła, ponieważ ekspansja metryki czasoprzestrzeni jest opisywana przez ogólną teorię względności w kategoriach sekwencji układów inercjalnych (ważnych tylko lokalnie), w przeciwieństwie do globalnej metryki Minkowskiego. Rozszerzanie szybsze niż światło jest efektem zintegrowanym w wielu lokalnych ramkach inercyjnych i jest dozwolone, ponieważ nie jest zaangażowana żadna pojedyncza ramka inercyjna. „Ograniczenie prędkości” światła obowiązuje tylko lokalnie. See Michal Chodorowski. Is space really expanding? A counterexample. „Concepts Phys”. 4, s. 17–34, 2007. DOI: 10.2478/v10005-007-0002-2. arXiv:astro-ph/0601171. Bibcode: 2007ONCP....4...15C.
- ↑ M. Weiss, What Causes the Hubble Redshift?, wpis w FAQ Fizyki (1994), dostępnym na stronie Johna Baeza.
- ↑ Ta zależność byłaby prawdziwa tylko we wszechświecie, w którym nie ma szczególnych prędkości. W przeciwnym razie przesunięcia ku czerwieni łączą się jako






































































