Z Wikipedii, wolnej encyklopedii
Rozkład Rayleigha
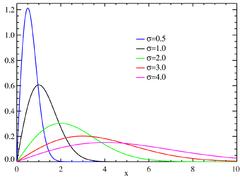
Gęstość prawdopodobieństwa
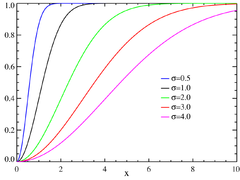
Dystrybuanta
Parametry
σ
>
0
{\displaystyle \sigma >0}
Nośnik
x
∈
[
0
;
∞
)
{\displaystyle x\in [0;\infty )}
Gęstość prawdopodobieństwa
x
exp
(
−
x
2
2
σ
2
)
σ
2
{\displaystyle {\frac {x\exp \left({\frac {-x^{2}}{2\sigma ^{2}}}\right)}{\sigma ^{2}}}}
Dystrybuanta
1
−
exp
(
−
x
2
2
σ
2
)
{\displaystyle 1-\exp \left({\frac {-x^{2}}{2\sigma ^{2}}}\right)}
Wartość oczekiwana (średnia)
σ
π
2
{\displaystyle \sigma {\sqrt {\frac {\pi }{2}}}}
Mediana
σ
ln
(
4
)
{\displaystyle \sigma {\sqrt {\ln(4)}}}
Moda
σ
{\displaystyle \sigma }
Wariancja
4
−
π
2
σ
2
{\displaystyle {\frac {4-\pi }{2}}\sigma ^{2}}
Współczynnik skośności
2
π
(
π
−
3
)
(
4
−
π
)
3
/
2
{\displaystyle {\frac {2{\sqrt {\pi }}(\pi -3)}{(4-\pi )^{3/2}}}}
Kurtoza
−
6
π
2
−
24
π
+
16
(
4
−
π
)
2
{\displaystyle -{\frac {6\pi ^{2}-24\pi +16}{(4-\pi )^{2}}}}
Entropia
1
+
ln
(
σ
2
)
+
γ
2
{\displaystyle 1+\ln \left({\frac {\sigma }{\sqrt {2}}}\right)+{\frac {\gamma }{2}}}
Funkcja tworząca momenty
1
+
σ
t
e
σ
2
t
2
/
2
π
2
(
erf
(
σ
t
2
)
+
1
)
{\displaystyle 1+\sigma t\,e^{\sigma ^{2}t^{2}/2}{\sqrt {\frac {\pi }{2}}}\left({\textrm {erf}}\left({\frac {\sigma t}{\sqrt {2}}}\right)\!+\!1\right)}
Funkcja charakterystyczna
1
−
σ
t
e
−
σ
2
t
2
/
2
π
2
(
erfi
(
σ
t
2
)
−
i
)
{\displaystyle 1\!-\!\sigma te^{-\sigma ^{2}t^{2}/2}{\sqrt {\frac {\pi }{2}}}\!\left({\textrm {erfi}}\!\left({\frac {\sigma t}{\sqrt {2}}}\right)\!-\!i\right)}
Rozkład Rayleigha – ciągły rozkład prawdopodobieństwa powstający jako rozkład długości wektora na płaszczyźnie, którego składowe są niezależnymi zmiennymi losowymi o rozkładzie normalnym . Jest rozkładem jednoparametrycznym i stanowi szczególny przypadek rozkładu Weibulla (kiedy parametr kształtu dla rozkładu Weibulla jest k=2, nazywany jest rozkładem Rayleigha).
Jest używany m.in. w elektronice . Odległość strumienia elektronów na kineskopie od celu (środka plamki luminoforu) jest funkcją niezależnych błędów o rozkładzie normalnym, związanych z odchylaniem poziomym i pionowym.
Rozkłady statystyczne
Rozkłady ciągłe
Rozkłady dyskretne