Masa spoczynkowa
Masa spoczynkowa (in. masa niezmiennicza lub po prostu masa) – wielkość fizyczna w fizyce relatywistycznej, charakteryzująca ciało bądź układ ciał, która nie zależy od układu odniesienia. W dowolnym układzie odniesienia, masa spoczynkowa jest wyznaczona przez energie i pędy wszystkich ciał. Jest to masa ciała mierzona w układzie odniesienia, w którym to ciało spoczywa.
Definicja[edytuj | edytuj kod]
Masa spoczynkowa ciała w dowolnym układzie odniesienia jest zdefiniowana jako:
Dla układu ciał jego masa spoczynkowa jest zdefiniowana jako:
W przypadku pojedynczego ciała w układzie spoczynkowym mamy i wtedy:
Dla cząstek bezmasowych (np. foton) spełnione jest równanie wiążące ich energię i pęd:
zatem zgodnie z definicją te cząstki mają masę spoczynkową równą zero (co uzasadnia nazwę cząstki bezmasowe).
Notacja czterowektorowa[edytuj | edytuj kod]
Czterowektor pędu ciała wyraża się wzorem:
gdzie więc:
Masę niezmienniczą można zapisać w tej notacji jako pierwiastek kwadratowy z:
Używając konwencji sumacyjnej można powyższe zapisać jako:
Dla układu ciał możemy obliczyć wypadkowy czterowektor pędu:
Dla tego układu:
Zastosowanie w fizyce cząstek elementarnych[edytuj | edytuj kod]
W fizyce cząstek elementarnych badanie rozkładu masy niezmienniczej jest standardową metodą poszukiwania nowych, nietrwałych cząstek. Wykorzystuje się fakt, że w rozpadzie cząstki zachowane są energia i pęd. Masa niezmiennicza układu cząstek powstałych w wyniku rozpadu jest więc równa masie spoczynkowej cząstki rozpadającej się. Metoda masy niezmienniczej polega na tym, że mając wiele przypadków możliwych rozpadów nowej cząstki, sporządzamy histogram masy niezmienniczej produktów. Jeżeli przypadki na histogramie grupują się wokół pewnej wartości, uznajemy, że istotnie obserwujemy zjawisko rozpadu, a wartość ta jest masą rozpadającego się obiektu.
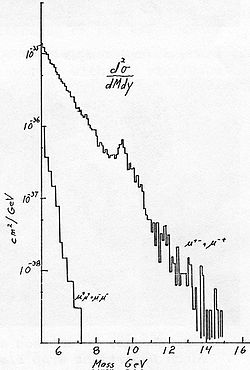
W praktyce często nie wiemy, które z obserwowanych produktów zderzenia pochodzą faktycznie z rozpadów poszukiwanej cząstki, a które powstały w pierwotnym zderzeniu, lub w rozpadach innych cząstek wtórnych. Dlatego sporządza się histogram masy niezmienniczej wszystkich wchodzących w grę kombinacji cząstek. Na takim histogramie poszukiwany sygnał będzie widoczny na tle pochodzącym od przypadkowych (nie pochodzących z rozpadu) kombinacji. W przykładzie na rysunku obok (rozkład masy niezmienniczej par mionów obserwowanych w eksperymencie E288) widzimy, na jednostajnie opadającym tle kombinacji przypadkowych, sygnał od par mionów pochodzących z rozpadu cząstki ϒ. Na podstawie tego wykresu zespół E288 ogłosił odkrycie nowej cząstki.
Innym zastosowaniem pojęcia masy niezmienniczej jest obliczenie maksymalnej masy obiektu, który może być wyprodukowany w zderzeniu cząstek o danych pędach i energiach: jest ona równa masie niezmienniczej układu przed zderzeniem. Rozpatrzmy na przykład proton o pędzie 400 GeV/c zderzający się z protonem spoczywającym. Przy tak wysokim pędzie energia protonu poruszającego się jest praktycznie równa pędowi (ściślej wynosi ok. 400,0011 GeV), energia protonu spoczywającego równa jest jego masie spoczynkowej (0,938 GeV). Całkowita energia cząstek przed zderzeniem wynosi więc 400,939 GeV, całkowity pęd 400 GeV/c, stąd masa niezmiennicza układu:
Tyle wynosi więc masa najcięższego obiektu, jaki można teoretycznie wyprodukować w takim zderzeniu.
Bibliografia[edytuj | edytuj kod]
- Ewa Skrzypczak, Zygmunt Szefliński: Fizyka jądra atomowego i cząstek elementarnych. Wyd. 2. Warszawa: PWN, 2002, s. 181. ISBN 83-01-13719-3.
















