Jednokierunkowa prędkość światła
Użycie terminu prędkość światła wymaga niekiedy rozróżnienia pomiędzy jednokierunkową i dwukierunkową prędkością światła. Prędkość jednokierunkowa pomiędzy źródłem a detektorem nie może zostać zmierzona niezależnie od metody synchronizacji zegarów źródła i detektora. Pomiar niezależny od synchronizacji możliwy jest jedynie na drodze w obie strony – od źródła do detektora i z powrotem. W ramach konwencji wybranej przez Einsteina (zobacz: synchronizacja standardowa) przyjmuje się, że prędkość jednokierunkowa wynosi tyle samo co dwukierunkowa. Postulat stałości jednokierunkowej prędkości światła w dowolnym inercjalnym układzie odniesienia jest podstawą szczególnej teorii względności, aczkolwiek wyniki wszelkich eksperymentów weryfikujących przewidywania tej teorii nie zależą od tego postulatu[1][2].
Zaproponowano eksperymenty mające na celu bezpośrednie przetestowanie stałości jednokierunkowej prędkości światła, jednak żaden z nich nie zakończył się powodzeniem[3]. Tego rodzaju eksperymenty pokazują w sposób bezpośredni, że synchronizacja metodą slow clock-transport jest równoważna synchronizacji standardowej. Aczkolwiek z tego nie wynika izotropia jednokierunkowej prędkości światła, ponieważ – jak pokazano – sama metoda slow clock-transport bazuje na tym założeniu[4]. W ogólności pokazano, że te wyniki są spójne z anizotropią jednokierunkowej prędkości światła pod warunkiem, że izotropia dwukierunkowej prędkości światła pozostaje zachowana[1][5].
W poniższym artykule pojęcie prędkość światła odnosi się ogólnie do prędkości rozchodzenia promieniowania elektromagnetycznego w próżni.
Dwukierunkowa prędkość światła[edytuj | edytuj kod]

Dwukierunkowa prędkość światła jest średnią prędkością światła na drodze od źródła do lustra i z powrotem. Ponieważ promień świetlny wraca do tego samego punktu, pomiar całego czasu wymaga jednego zegara ustawionego w miejscu startu. Z tego powodu dwukierunkowa prędkość światła może zostać obliczona niezależnie od metody synchronizacji zegarów. Każdy pomiar, w którym światło porusza się po drodze zamkniętej, jest uważany za pomiar dwukierunkowej prędkości światła.
Wiele testów szczególnej teorii względności, takich jak doświadczenie Michelsona-Morleya lub doświadczenie Kennedy’ego-Thorndike’a, wykazało w granicach pewnej dokładności, że w inercjalnych układach odniesienia dwukierunkowa prędkość światła jest izotropowa i niezależna od drogi zamkniętej, po której porusza się światło. Eksperymenty typu Michelsona-Morlaya nie wykorzystują zewnętrznego zegara do bezpośredniego pomiaru prędkości światła, ale porównują czasy, w których względnie prostopadłe odcinki są pokonywane przez rozszczepiony promień świetlny. Tego rodzaju eksperymenty są niekiedy nazywane testami anizotropii zegara, ponieważ ramiona interferometru mogą być interpretowane jako zegary świetlne o określonej częstotliwości[6].
Ponieważ w 1983 roku metr został zdefiniowany jako odległość pokonywana przez światło w próżni w czasie 1/299 792 458 sekundy[a], prędkość światła nie może być obecnie mierzona w jednostkach układu SI. Aczkolwiek w tej sytuacji długość metra może być eksperymentalnie porównywana z innymi jednostkami długości.
Jednokierunkowa prędkość światła[edytuj | edytuj kod]
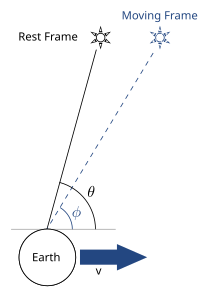
Chociaż średnia prędkość światła na drodze w dwóch kierunkach może zostać zmierzona, prędkość w jednym kierunku pozostaje niezdefiniowana bez określenia fizycznego sensu „jednoczesności” dwóch odległych zdarzeń. Przy pomiarze czasu, w jakim światło pokonuje określony odcinek, konieczne jest założenie, że czas startu promienia świetlnego jest mierzony w tej samej skali czasowej, co czas dotarcia promienia do końca odcinka. Wymaga to dwóch zsynchronizowanych zegarów na obydwu końcach odcinka lub możliwości natychmiastowego przesłania sygnału pomiędzy końcami odcinka. Nie są znane żadne metody pozwalające na natychmiastową transmisję informacji, z tego powodu każdy jednokierunkowy pomiar prędkości światła jest uzależniony od metody synchronizacji zegarów. Jest to kwestia konwencji. Transformacja Lorentza została zdefiniowana w taki sposób, że jednokierunkowa prędkość światła staje się niezależna od wyboru inercjalnego układu odniesienia[7].
Niektórzy autorzy, np. Mansouri i Sexl (1977)[8][9], jak również Will (1992)[10], argumentowali, że ten problem nie ma wpływu na testy izotropii jednokierunkowej prędkości światła, na przykład ze względu na zmiany kierunku względem preferowanego układu (eteru) Σ. Wspomniani autorzy opierają swoje analizy na pewnej interpretacji RMS w odniesieniu do eksperymentów w których światło pokonuje jednokierunkową drogę oraz eksperymentów wykorzystujących slow clock-transport. Co więcej, Will dodał, że teorie eteru mogą zostać uzgodnione z teorią względności tylko poprzez wprowadzenie hipotezy ad hoc[10].
Natomiast inni autorzy, tacy jak Zhang (1995, 1997)[1][11] i Anderson (1998)[2], pokazali, że ta interpretacja jest niepoprawna. Na przykład Anderson zwracał uwagę, że konwencja równoczesności musi zostać rozpatrzona już w preferowanym układzie, więc wszystkie założenia odnośnie do izotropii jednokierunkowej prędkości światła i innych prędkości w tym układzie są również konwencjonalne. W związku z tym RMS pozostaje użyteczną ramą teoretyczną w zakresie analizy testów lorentzowskiej niezmienniczości oraz izotropii dwukierunkowej, ale nie jednokierunkowej prędkości światła. Ponadto, bazując na uogólnieniu transformacji Lorentza dopuszczającym anizotropię jednokierunkowej prędkości światła, Zhang i Anderson wykazali, że wszystkie zjawiska oraz wyniki doświadczalne kompatybilne z transformacją Lorentza i izotropią jednokierunkowej prędkości światła muszą być również kompatybilne z transformacjami zachowującymi stałość i izotropię dwukierunkowej prędkości światła (nawet w przypadkach dopuszczających anizotropię jednokierunkowej prędkości światła).
Synchronizacja zegarów[edytuj | edytuj kod]
Sposób synchronizacji rozdzielonych przestrzennie zegarów może mieć wpływ na pomiar wszelkich zależnych od czasu wielkości, takich jak pomiary prędkości lub przyśpieszeń. W eksperymentach testujących izotropię konwencja równoczesności dwóch przestrzennie rozdzielonych zdarzeń często nie jest jawnie ustalana, ale wprowadzana (implicite) w transformacji współrzędnych lub w postaci zakładanych praw fizyki[2].
Synchronizacja standardowa[edytuj | edytuj kod]
Ta metoda synchronizacji bazuje na założeniu, że jednokierunkowa prędkość światła równa jest dwukierunkowej prędkości światła. Jeżeli sygnał wysłany z punktu A w czasie dociera do punktu B w czasie i powraca do A w czasie to wówczas stosując niniejszą konwencję:
Slow clock-transport[edytuj | edytuj kod]
Łatwo pokazać, że jeżeli dwa zegary zostaną zsynchronizowane w tym samym punkcie przestrzeni A, następnie jeden z nich zostanie wprawiony w ruch po drodze zamkniętej na odcinku AB i z powrotem, zegary te nie będą dłużej zsynchronizowane w punkcie A (z uwagi na dylatację czasu). Fakt ten był wielokrotnie sprawdzany doświadczalnie i ma bliski związek z paradoksem bliźniąt[12][13].
Natomiast stopień rozsynchronizowania zegarów przy ich wzajemnym przesuwaniu jest tym mniejszy, im mniejsza jest ich prędkość względna. Z tego wynika, że dwa zegary mogą pozostać zsynchronizowane z dowolnie dużą dokładnością pod warunkiem, że będą przesuwane dostatecznie wolno. Jeśli przyjmiemy, że przy tego rodzaju przesunięciu oba zegary pozostają zsynchronizowane (z pewną dokładnością) cały czas (nawet w czasie, gdy są rozdzielone), to tego rodzaju metoda może zostać wykorzystana do synchronizacji rozdzielonych przestrzennie zegarów. W granicy prędkości przesuwania zegarów dążącej do zera ta metoda jest teoretycznie i eksperymentalnie równoważna synchronizacji standardowej[4].
Aczkolwiek wpływ dylatacji czasu nie może zostać pominięty z punktu widzenia innego układu odniesienia S poruszającego się względem obydwu zegarów. Takie zegary pozostaną zsynchronizowane we własnych układach, ale nie w układzie S. To zjawisko nazywane względną równoczesnością zdarzeń występuje również przy zastosowaniu synchronizacji standardowej[14]. W związku z tym, sprawdzenie równoważności tych dwóch sposobów synchronizacji jest istotne i pewne eksperymenty potwierdziły ją z wysoką dokładnością.
Jeżeli założymy, że jednokierunkowa prędkość światła jest anizotropowa, współczynnik dylatacji czasu przyjmie formę z parametrem κ pomiędzy –1 a 1[15]. Pociąga to nowy czynnik liniowy co oznacza, że dylatacja czasu w takim przypadku nie może być ignorowana dla małych prędkości i synchronizacja metodą slow clock-transport nie wykryje tej anizotropii. Zatem jest ona równoważna synchronizacji Einsteina.
Synchronizacje niestandardowe[edytuj | edytuj kod]
Jak pokazał Hans Reichenbach i Adolf Grünbaum, synchronizacja standardowa jest tylko szczególnym przypadkiem znacznie szerszej klasy możliwych synchronizacji, dla których stałość dwukierunkowej prędkości światła jest zachowana, ale niezmienniczość jednokierunkowej prędkości światła nie musi być zachowana. Formuła synchronizacji standardowej została zmodyfikowana poprzez zastąpienie ½ parametrem ε[4]:
ε może przyjmować wartości z przedziału (0,1). Pokazano, że klasa powyższych synchronizacji jest empirycznie równoważna uogólnieniu transformacji Lorentza (zobacz: uogólnienie transformacji Lorentza dopuszczające anizotropię jednokierunkowej prędkości światła).
W związku z dowiedzioną eksperymentalnie równoważnością synchronizacji standardowej oraz synchronizacji metodą slow clock-transport, która wymaga wiedzy o dylatacji czasu poruszającego się zegara, synchronizacje niestandardowe również muszą jej dotyczyć. Faktycznie, zwracano uwagę, że dylatacja czasu zależy od konwencjonalności jednokierunkowych prędkości użytych we wzorze wyrażającym dylatacje[16]. Dylatacja czasu może zostać zmierzona po zsynchronizowaniu dwóch oddalonych zegarów A i B za pomocą trzeciego poruszającego się na ich linii zegara C. Zmiana konwencji synchronizacji A i B wpływa na zmianę dylatacji czasu zegara C (jak przy pomiarze jednokierunkowej prędkości światła). Taka sama konwencjonalność występuje również przy pomiarze dylatacji czasu z wykorzystaniem efektu Dopplera[17]. Tylko w przypadku, gdy dylatacja czasu jest mierzona na drodze zamkniętej, wynik nie jest uzależniony od konwencji synchronizacji i może zostać jednoznacznie zmierzony (tak jak w przypadku dwukierunkowej prędkości światła). Dylatacja czasu na drodze zamkniętej została zmierzona w doświadczeniu Hafelea-Keatinga oraz w testach dylatacji czasu poruszających się cząstek elementarnych, takich jak eksperyment Baileya (1977)[18]. Zatem tzw. paradoks bliźniąt występuje we wszystkich transformacjach zachowujących stałość dwukierunkowej prędkości światła.
Dynamika i inercjalne układy odniesienia[edytuj | edytuj kod]
Argumentowano przeciwko konwencjonalności jednokierunkowej prędkości światła, odnosząc się do bliskiego związku tej koncepcji z dynamiką, prawami ruchu i sposobem zdefiniowania inercjalnego układu odniesienia[4]. Salmon opisał kilka rodzajów tego typu argumentów bazujących na zasadzie zachowania pędu, z której wynika, że dwa jednakowe ciała, które są jednakowo przyśpieszane w przeciwnych kierunkach, powinny poruszać się z takimi samymi jednokierunkowymi prędkościami[19]. Podobnie Ohanian argumentował, że inercjalne układy odniesienia są zdefiniowane w taki sposób, aby prawa Newtona były zachowane w pierwszym przybliżeniu. W związku z tym, ponieważ prawa ruchu przewidują izotropię jednokierunkowej prędkości poruszających się ciał na skutek takiego samego przyśpieszenia i ponieważ eksperymentalnie wykazano równoważność synchronizacji standardowej i metody slow clock-transport, wydaje się konieczne i bezpośrednio zmierzone, że jednokierunkowa prędkość światła jest izotropowa w inercjalnym układzie odniesienia. W przeciwnym razie zarówno pojęcie inercjalnego układu odniesienia, jak i prawa ruchu musiałyby przyjąć znacznie bardziej skomplikowaną formę obejmującą anizotropię współrzędnych[20][21].
Natomiast inni autorzy twierdzili, że nie ma zasadniczej sprzeczności pomiędzy powyższymi argumentami a konwencjonalnością jednokierunkowej prędkości światła[4]. Salmon argumentował, że zasada zachowania pędu w swojej standardowej formie zakłada izotropię jednokierunkowej prędkości światła od samego początku, co wiąże się praktycznie z taką samą konwencjonalnością, jak w wypadku jednokierunkowej prędkości światła, więc użycie tego jako argumentu opiera się na błędnym kole[19]. W odpowiedzi do Ohaniana, Macdonald i Martinez argumentowali, że nawet pomimo bardziej skomplikowanej formy praw fizyki pojawiającej się przy przyjęciu niestandardowej synchronizacji, one wciąż stanowią spójną metodę opisu. Argumentowali również, że nie jest konieczne definiowanie inercjalnego układu odniesienia w terminach praw Newtona, ponieważ możliwe są inne sposoby[22][23]. Co więcej, Iyer i Prabhu wprowadzili rozróżnienie pomiędzy „izotropowym układem inercjalnym” ze standardową synchronizacją a „anizotropowym układem inercjalnym” z niestandardową synchronizacją[24].
Eksperymenty, w których próbowano zmierzyć jednokierunkową prędkość światła[edytuj | edytuj kod]
Eksperymenty, w których zakładano wykorzystanie jednokierunkowego sygnału świetlnego[edytuj | edytuj kod]
Eksperyment Greavesa, Rodrigueza i Ruiz-Camachoa[edytuj | edytuj kod]
W opublikowanym w październiku 2009 roku wydaniu „American Journal of Physics” Greaves, Rodriguez i Ruiz-Camacho donieśli o nowej metodzie pomiaru jednokierunkowej prędkości światła[25]. W czerwcu 2013 w tym samym czasopiśmie Hankins, Rackson i Kim opisali swoją wersje eksperymentu Greaves’a, w której otrzymali wyższą dokładność wyniku[26]. Doświadczenie polega na pomiarze czasu przelotu światła lasera przy pomocy ruchomego detektora podłączonego do aparatury za pomocą przewodu wprowadzającego stałe opóźnienie sygnału. Stała proporcjonalność czasu do odległości, jaką pokonuje światło, oznacza stałość jednokierunkowej prędkości światła.
J. Finkelstein twierdził, że eksperyment Greaves’a w rzeczywistości mierzy jedynie prędkość w obydwie strony (dwukierunkową prędkość światła). Zwracał uwagę, że w założeniu o stałym opóźnieniu sygnału w przewodzie biegnącym od detektora zawiera się implicite konwencja synchronizacji zegarów. Z tego powodu takie eksperymenty mierzą tak naprawdę średnią prędkość sygnału na odcinku od źródła (lasera) do detektora i sygnału powrotnego, transmitowanego przy pomocy przewodu z powrotem w okolice lasera. Kilku innych fizyków zgłosiło podobne zastrzeżenia[27].
W listopadowym wydaniu „Indian Journal of Physics” z 2012 roku Md.F. Ahmed opublikował obszerny przegląd jednokierunkowych i dwukierunkowych eksperymentów testujących izotropię prędkości światła[28].
Eksperymenty, w których światło pokonuje jednokierunkową drogę[edytuj | edytuj kod]

Wiele eksperymentów mających na celu pomiar jednokierunkowej prędkości światła lub jej zmianę w zależności od kierunku było (a czasem nadal są) wykonywane dla światła pokonującego jednokierunkową drogę[29]. Twierdzono, że tego rodzaju eksperymenty mierzą jednokierunkową prędkość światła w sposób niezależny od konwencji synchronizacji zegarów. Natomiast pokazano, że w rzeczywistości mierzą one jedynie dwukierunkową prędkość światła, ponieważ wyniki uzyskane w ramach tych doświadczeń są spójne z uogólnioną transformacją Lorentza, obejmującą synchronizację z anizotropią jednokierunkowej prędkości światła przy zachowaniu izotropii dwukierunkowej prędkości światła (zobacz: jednokierunkowa prędkość światła i uogólniona transformacja Lorentza)[1].
Tego rodzaju doświadczenia potwierdziły zgodność metody slow clock-transport i synchronizacji standardowej[2]. Pomimo że część autorów twierdziła, że jest to wystarczające do udowodnienia izotropii jednokierunkowej prędkości światła[9][10], zostało pokazane, że tego rodzaju doświadczenia nie mogą, w jakimkolwiek wyraźnym sensie, zmierzyć (an)izotropii jednokierunkowej prędkości światła, chyba że inercjalny układ odniesienia i współrzędne zostaną zdefiniowane od samego początku w taki sposób, że współrzędne czasu i przestrzeni, jak również slow clock-transport, będą opisywane w sposób izotropowy[2] (zobacz: dynamika i inercjalne układy odniesienia oraz jednokierunkowa prędkość światła). Niezależnie od tej różnicy zdań, zaobserwowana zgodność pomiędzy tymi dwoma metodami synchronizacji jest ważna z punktu widzenia przewidywań szczególnej teorii względności, ponieważ transportowany zegar podlega dylatacji czasu (która jest zależna od synchronizacji) w niezwiązanym z nim układzie odniesienia (zobacz: slow clock-transport oraz synchronizacje niestandardowe).
Eksperyment JPL[edytuj | edytuj kod]
Eksperyment JPL został przeprowadzony przez NASA w 1990 roku w Jet Propulsion Laboratory. Polegał na pomiarze czasu propagacji sygnału świetlnego w światłowodowym łączu na odcinku 21 km pomiędzy dwoma maserami wodorowymi. Próbowano wykryć anizotropię spowodowaną zmianą pozycji Ziemi na orbicie[30]. W 1992 roku wyniki eksperymentu zostały przeanalizowane przez Clifforda Willa, który stwierdził, że rzeczywiście zmierzono jednokierunkową prędkość światła[10].
W 1997 roku eksperyment został ponownie przeanalizowany przez Zhanga, który pokazał, że w rzeczywistości została zmierzona jedynie dwukierunkowa prędkość światła[31].
Pomiar Rømera[edytuj | edytuj kod]
Pierwszy w historii pomiar prędkości światła został wykonany przez Olea Christensena Rømera. Metoda Rømera polegała na obserwacji ruchów księżyców Jowisza w różnych porach roku, co pozwalało na oszacowanie czasu, w jakim światło przebiega odległość równą średnicy orbity Ziemi. Zhang wykazał, że metoda Rømera nie pozwala na wyznaczenie jednokierunkowej prędkości światła, niezależnie od konwencji synchronizacji zegarów, ponieważ system księżyców Jowisza pełni w pomiarze Rømera rolę analogiczną do powoli przesuwanego zegara[32].
Australijski fizyk Karlov również wykazał, że Rømer dokonywał pomiaru prędkości światła przy niejawnym założeniu, że prędkość światła w obydwu kierunkach jest taka sama[33][34].
Inne doświadczenia porównujące synchronizacje Einsteina i slow clock-transport[edytuj | edytuj kod]
| Eksperyment | Rok | ||
|---|---|---|---|
| Doświadczenie Mössbauera | lata 60. XX w. | Promieniowanie gamma wysyłano z obwodu obracającej się tarczy w kierunku jej środka. Oczekiwano, że ewentualna anizotropia prędkości światła spowoduje przesunięcie dopplerowskie. | |
| Vessot i inni[35] | 1980 | Porównanie czasu przelotu sygnału w obie strony podczas misji Gravity Probe A. | |
| Riis i inni[36] | 1988 | Porównanie częstotliwości dwufotonowej absorpcji w szybkim strumieniu cząstek z częstotliwością stacjonarnego absorbera. Kierunek wiązki zmieniano względem gwiazd stałych. | |
| Nelson i inni[37] | 1992 | Porównanie częstotliwości masera wodorowego i impulsów światła laserowego. Długość ścieżki, na której wykonywano pomiar, to 26 km. | |
| Wolf & Petit[38] | 1997 | Porównanie czasów mierzonych przez masery wodorowe na Ziemi i czasów mierzonych przez cezowe i rubidowe zegary na pokładach 25 satelitów GPS. |
Eksperymenty, które można przeprowadzić, dotyczące jednokierunkowej prędkości światła[edytuj | edytuj kod]

Chociaż nie jest możliwe zmierzenie jednokierunkowej prędkości światła niezależnie od konwencji synchronizacji zegarów, istnieje możliwość wykonania pomiarów zmian jednokierunkowej prędkości światła, np. w zależności od ruchu źródła. Przykładem jest eksperyment Sittera z gwiazdą podwójną (1913), powtórzony również przez K. Brechera (1977)[39], w którym analizowano promieniowanie X emitowane w układzie gwiazd podwójnych, a także doświadczenie Alvägera (1963)[40] wykonane w warunkach naziemnych. Wszystkie te eksperymenty wykazały (w granicach pewnych dokładności), że wynik pomiaru jednokierunkowej prędkości światła w inercjalnym układzie odniesienia jest niezależny od prędkości źródła. W tego rodzaju eksperymentach synchronizacja rozdzielonych przestrzennie zegarów nie jest potrzebna, ponieważ mierzona jest jedynie zmiana prędkości.
Obserwacje promieniowania pochodzącego z odległych zjawisk astronomicznych takich jak rozbłyski gamma pokazały, że prędkość fotonów jest taka sama bez względu na energie[41]. Efekty tego typu były wielokrotnie analizowane w ramach Standard-Model Extension i są spójne z przewidywaniami teorii względności.
Eksperymenty analizowane w ramach Standard-Model Extension, dotyczące jednokierunkowej i dwukierunkowej prędkości światła[edytuj | edytuj kod]
Podczas gdy powyższe eksperymenty zostały przeanalizowane z użyciem uogólnionej transformacji Lorentza, takiej jak np. w Robertson-Mansouri-Sexl framework, wiele współczesnych testów doświadczalnych bazuje na Standard-Model Extension (SME). Jest to teoria obejmująca wszystkie możliwe naruszenia niezmienniczości Lorentza, nie tylko w szczególnej teorii względności, ale również w modelu standardowym i ogólnej teorii względności. (An)izotropia jednokierunkowej oraz dwukierunkowej prędkości światła została opisana za pomocą zestawu współczynników (macierzy 3x3) [42].
Serie eksperymentów przeprowadzanych od 2002 roku miały na celu przetestowanie wszystkich tych współczynników, przy użyciu m.in. symetrycznych i asymetrycznych rezonatorów optycznych. Do roku 2013 żadne naruszenia niezmienności Lorentza nie zostały wykryte, co więcej dowiedziono górnego ograniczenia dla naruszeń wszystkich parametrów na poziomie: i
Natomiast Kostelecky zwrócił uwagę na częściowo konwencjonalny charakter tych wielkości, twierdząc, że tego rodzaju odchylenia prędkości światła mogą zostać usunięte poprzez odpowiednie redefinicje pola i transformacji współrzędnych. Jednakże to nie pozwala na usunięcie naruszeń niezmienniczości Lorentza per se, ponieważ takie redefinicje przesuwają jedynie naruszenie do innego sektora SME. Z tego powodu eksperymenty analizowane w ramach SME pozostają poprawnymi testami niezmienniczości Lorentza[42].
Teorie, w których jednokierunkowa prędkość światła nie jest równa dwukierunkowej prędkości światła[edytuj | edytuj kod]
Teorie równoważne szczególnej teorii względności[edytuj | edytuj kod]
Teoria eteru Lorentza[edytuj | edytuj kod]

W 1904 i 1905 roku Hendrik Lorentz i Henri Poincaré zaproponowali teorię wyjaśniającą efekty związane z ruchem obiektów względem eteru jako wynik zmiany długości obiektów fizycznych (skrócenie Lorentza) i szybkości działania poruszających się zegarów. Podczas ruchu względem eteru przedmioty powinny ulegać skróceniu w kierunku ruchu, natomiast zegary ulegać spowolnieniu. Zatem w tej teorii powoli przesuwane zegary nie pozostają zsynchronizowane, chociaż efekt ten nie może zostać empirycznie wykryty. Równania opisujące teorie Lorentza znane są pod nazwą transformacji Lorentza. W 1905 roku te same transformacje stały się podstawowymi równaniami szczególnej teorii względności Einsteina, który zaproponował równoważną teorię bez odwoływania się do koncepcji eteru.
W teorii Lorentza jednokierunkowa prędkość światła jest równa dwukierunkowej tylko w układzie eteru, w innych układach taka równość nie zachodzi ze względu na stałość prędkości światła względem eteru. Natomiast różnica pomiędzy jednokierunkową i dwukierunkową prędkością światła jest niemożliwa do zaobserwowania z powodu wpływu ruchu na działanie zegarów i skrócenie długości. Z powyższego powodu, również synchronizacja Einsteina-Poincarégo może zostać zastosowana w tym modelu, wówczas jednokierunkowa prędkość światła staje się izotropowa we wszystkich układach odniesienia.
Nawet pomimo tego, że teoria Lorentza jest empirycznie równoważna szczególnej teorii względności, nie jest dłużej stosowana z powodów filozoficznych oraz z powodu rozwoju ogólnej teorii względności.
Uogólnienia transformacji Lorentza dopuszczające anizotropię jednokierunkowej prędkości światła[edytuj | edytuj kod]
Konwencja synchronizacji zaproponowana przez Reichenbacha i Grünbauma, nazywana przez nich ε-synchronizacją, została w późniejszym czasie rozwinięta przez autorów takich jak Edwards (1963)[43], Winnie (1970)[16], Anderson i Stedman (1977), którzy przeformułowali transformacje Lorentza w sposób nie wpływający na fizyczne przewidywania teorii[1][2]. Na przykład Edwards zastąpił postulat Einsteina mówiący, że jednokierunkowa prędkość światła jest stała w każdym układzie inercjalnym, postulatem:
Dwukierunkowa prędkość światła w próżni mierzona w dwóch poruszających się względem siebie układach (inercjalnych) jest taka sama niezależnie od jakichkolwiek założeń dotyczących jednokierunkowej prędkości światła[43].
Średnia prędkość światła na drodze w obydwie strony pozwala więc na empiryczną weryfikowalność dwukierunkowej prędkości światła, natomiast jednokierunkowa prędkość świtała w przeciwnych kierunkach przyjmuje wartości:
gdzie κ może przyjmować wartości z przedziału (0,1). W skrajnych przypadkach, gdy κ jest bliskie wartości 1, światło może poruszać się w jednym kierunku prawie natychmiastowo, pod warunkiem, że średnia prędkość na całej drodze w obydwie strony wynosi c. Za Edwardsem, Winniem i Andersonem uogólnienie transformacji Lorentza przyjmuje postać[2]:
gdzie κ i κ' to wektory synchronizacji w układach odpowiednio S i S′. Powyższa transformacja pokazuje, że jednokierunkowa prędkość światła jest konwencjonalna we wszystkich układach odniesienia, przy czym dwukierunkowa prędkość światła pozostaje niezmiennicza. Zastosowanie κ = 0 prowadzi do standardowej transformacji Lorentza z synchronizacją Einsteina. Jak wykazali Edwards, Winnie i Mansouri-Sexl, poprzez odpowiednie przegrupowanie parametrów synchronizacji można otrzymać nawet pewien rodzaj „absolutnej równoczesności”, odtwarzając w ten sposób podstawowe założenia teorii eteru Lorentza. W jedynym „preferowanym” układzie jednokierunkowa prędkość światła jest izotropowa, podczas gdy wszystkie inne układu przejmują wielkości z „preferowanego” układu za pomocą „synchronizacji zewnętrznej”[8].
Wszystkie przewidywania wyprowadzone z takiej transformacji są empirycznie równoważne standardowej transformacji Lorentza; jedyna różnica polega na innym niż u Einsteina zdefiniowaniu równoczesności rozdzielonych przestrzennie zdarzeń[42].
Teorie, które nie są równoważne szczególnej teorii względności[edytuj | edytuj kod]
Teorie testowe[edytuj | edytuj kod]
Rozwinięto wiele teorii pozwalających na oszacowanie stopnia w jakim wyniki doświadczalne różnią się od przewidywań teorii względności. Tego rodzaju teorie nazywane są teoriami testowymi, należy do nich m.in. Robertson and Mansouri-Sexl framework (RMS)[8]. Jak dotąd wszystkie wyniki doświadczalne zgadzają się z przewidywaniami szczególnej teorii względności w granicach niepewności pomiaru.
Innym rodzajem teorii tego rodzaju jest Standard-Model Extension (SME), obejmujący szeroki zbiór parametrów charakteryzujących możliwe naruszenia niezmienniczości Lorentza w szczególnej teorii względności, ogólnej teorii względności i w modelu standardowym. Niektóre z tych parametrów dotyczą anizotropii dwukierunkowej i jednokierunkowej prędkości światła. Zwracano uwagę, że ewentualne naruszenia izotropii prędkości światła mogłyby zostać usunięte poprzez redefinicje pola i transformacji współrzędnych. Aczkolwiek nie pozwala to na usunięcie naruszeń niezmienniczości Lorentza per se, ponieważ takie redefinicje przesuwają jedynie naruszenie do innego sektora SME (zobacz: Eksperymenty analizowane w ramach Standard-Model Extension, dotyczące jednokierunkowej i dwukierunkowej prędkości światła)[42].
Teorie eteru[edytuj | edytuj kod]
Przed 1887 rokiem powszechnie sądzono, że fala świetlna rozchodzi się ze stałą prędkością względem hipotetycznego ośrodka zwanego eterem. W układzie obserwatora poruszającego się względem eteru powinno to powodować niewielką różnicę w dwukierunkowej prędkości światła (ze względu na kierunek odcinka pokonywanego przez promień świetlny w stosunku do ruchu względem eteru). W 1887 roku doświadczenie Michelsona-Morleya pokazało, że mierzona wartość dwukierunkowej prędkości światła jest stała, bez względu na kierunek pomiaru i prędkość względem eteru. W tamtych czasach oczywistym wyjaśnieniem wyniku tego eksperymentu była hipoteza dylatacji czasu i kontrakcji długości obiektów poruszających się względem eteru.
Preferowany układ odniesienia[edytuj | edytuj kod]
Preferowany układ odniesienia to taki układ odniesienia, w którym prawa fizyki przyjmują szczególną formę. Możliwość wykonania pomiaru, pokazującego, że jednokierunkowa prędkość światła jest różna od dwukierunkowej prędkości światła, pozwala na wyróżnienie jednego układu odniesienia. Jest nim ten układ odniesienia, w którym dwukierunkowa prędkość światła jest równa jednokierunkowej prędkości światła.
W szczególnej teorii względności Einsteina wszystkie inercjalne układy odniesienia są równoważne i nie istnieje układ preferowany. Istnieją teorie, takie jak teoria eteru Lorentza, które są empirycznie i matematycznie równoważne szczególnej teorii względności, ale wprowadzają preferowany układ odniesienia. W tego rodzaju teoriach, aby zapewnić zgodność z doświadczeniem, preferowany układ odniesienia musi być niewykrywalny. Innymi słowy, preferowany układ odniesienie istnieje jedynie teoretycznie, jako nieobserwowalna własność teorii; w praktyce, wszystkie inercjalne układy odniesienia pozostają empirycznie równoważne, tak jak w szczególnej teorii względności.
Uwagi[edytuj | edytuj kod]
- ↑ 17th General Conference on Weights and Measures (1983), Resolution 1.
Przypisy[edytuj | edytuj kod]
- ↑ a b c d e Zhang 1997 ↓.
- ↑ a b c d e f g Anderson R., Vetharaniam I., Stedman G.E., Conventionality of synchronisation, gauge dependence and test theories of relativity, „Physics Reports”, 3–4, 295, 1998, s. 93–180, DOI: 10.1016/S0370-1573(97)00051-3, Bibcode: 1998PhR...295...93A (ang.).
- ↑ Michael Tooley: Time, tense, and causation. Oxford University Press, 2000, s. 350. ISBN 978-0-19-825074-6. (ang.).
- ↑ a b c d e Janis A., Conventionality of Simultaneity [online], 2010 (ang.).
- ↑ Jong-Ping Hsu, Yuan-Zhong Zhang, Lorentz and Poincaré Invariance: 100 Years of Relativity, World Scientific, 2001, ISBN 978-981-02-4721-8 (ang.).
- ↑ Will C.M, Special Relativity: A Centenary Perspective, [w:] T. Damour i inni red., Poincare Seminar 2005, Basel: Birkhauser, 2005, s. 33–58, DOI: 10.1007/3-7643-7436-5_2, Bibcode: 2006eins.book...33W, arXiv:gr-qc/0504085 (ang.).
- ↑ Zhang 1997 ↓, s. 24.
- ↑ a b c Mansouri R., Sexl R.U., A test theory of special relativity. I: Simultaneity and clock synchronization, „Gen. Rel. Gravit.”, 8 (7), 1977, s. 497–513, DOI: 10.1007/BF00762634, Bibcode: 1977GReGr...8..497M (ang.).
- ↑ a b Mansouri R., Sexl R.U., A test theory of special relativity: II. First order tests, „Gen. Rel. Gravit.”, 8 (7), 1977, s. 515–524, DOI: 10.1007/BF00762635, Bibcode: 1977GReGr...8..515M (ang.).
- ↑ a b c d Will, Clifford M. Clock synchronization and isotropy of the one-way speed of light. „Physical Review D”. 45 (2), s. 403–411, 1992. DOI: 10.1103/PhysRevD.45.403. Bibcode: 1992PhRvD..45..403W. (ang.).
- ↑ Zhang, Yuan Zhong. Test theories of special relativity. „General Relativity and Gravitation”. 27 (5), s. 475–493, 1995. DOI: 10.1007/BF02105074. Bibcode: 1995GReGr..27..475Z. (ang.).
- ↑ Joseph C. Hafele, Richard E. Keating, Around-the-World Atomic Clocks: Predicted Relativistic Time Gains, „Science”, 177 (4044), 1972, s. 166–168, DOI: 10.1126/science.177.4044.166, PMID: 17779917, Bibcode: 1972Sci...177..166H (ang.).
- ↑ C.O. Alley, Introduction to some fundamental concepts of general relativity and to their required use in some modern timekeeping systems, „NASA Goddard Space Flight Center, Proc. of the 13th Ann. Precise Time and Time Interval (PTTI) Appl. and Planning Meeting”, 1982, s. 687–724 (ang.).
- ↑ Synchronization by slow clock-transport. W: Giulini, Domenico: Special Relativity: A First Encounter. 100 years since Einstein. Oxford University Press, 2005. ISBN 0-19-162086-6. (ang.).
- ↑ Anderson, Vetharaniam. Conventionality of synchronisation, gauge dependence and test theories of relativity. „Physics Reports”. 295 (3–4), s. 93–180, March 1998. DOI: 10.1016/S0370-1573(97)00051-3. Bibcode: 1998PhR...295...93A.
- ↑ a b Winnie J.A.A. Special Relativity without One Way Velocity Assumptions. „Philosophy of Science”. 37 (2), s. 81–99, 223–38, 1970. DOI: 10.1086/288296. JSTOR: 186029. (ang.).
- ↑ Debs Talal A., Redhead Michael L.G., The twin „paradox” and the conventionality of simultaneity, „American Journal of Physics”, 64 (4), 1996, s. 384–392, DOI: 10.1119/1.18252, Bibcode: 1996AmJPh..64..384D (ang.).
- ↑ J. Bailey i inni, Measurements of relativistic time dilatation for positive and negative muons in a circular orbit, „Nature”, 268 (5618), 1977, s. 301–305, DOI: 10.1038/268301a0, Bibcode: 1977Natur.268..301B (ang.).
- ↑ a b Wesley C. Salmon. The Philosophical Significance of the One-Way Speed of Light. „Noûs”. 11 (3), s. 253–292, 1977. DOI: 10.2307/2214765. JSTOR: 221476. (ang.).
- ↑ Ohanian, Hans C. The role of dynamics in the synchronization problem. „American Journal of Physics”. 72 (2), s. 141–148, 2004. DOI: 10.1119/1.1596191. Bibcode: 2004AmJPh..72..141O. (ang.).
- ↑ Ohanian, Hans C. Reply to „Comment(s) on 'The role of dynamics in the synchronization problem’,” by A. Macdonald and A.A. Martínez. „American Journal of Physics”. 73 (5), s. 456–457, 2005. DOI: 10.1119/1.1858449. Bibcode: 2005AmJPh..73..456O. (ang.).
- ↑ MacDonald, Alan. Comment on „The role of dynamics in the synchronization problem,” by Hans C. Ohanian. „American Journal of Physics”. 73 (5), s. 454–455, 2004. DOI: 10.1119/1.1858448. Bibcode: 2005AmJPh..73..454M. (ang.).
- ↑ Martínez, Alberto A. Conventions and inertial reference frames. „American Journal of Physics”. 73 (5), s. 452–454, 2005. DOI: 10.1119/1.1858446. Bibcode: 2005AmJPh..73..452M. (ang.).
- ↑ Iyer Chandru, Prabhu G.M., A constructive formulation of the one-way speed of light, „American Journal of Physics”, 78 (2), 2010, s. 195–203, DOI: 10.1119/1.3266969, Bibcode: 2010AmJPh..78..195I, arXiv:1001.2375 (ang.).
- ↑ 111Greaves E.D., Rodríguez An Michel, Ruiz-Camacho J. A one-way speed of light experiment. „American Journal of Physics”. 77 (10), s. 894–896, 2009. DOI: 10.1119/1.3160665. Bibcode: 2009AmJPh..77..894G. (ang.).
- ↑ Hankins A., Rackson C., Kim W.J., Photon charge experiment, „Am. J. Phys.”, 81 (6), 2013, s. 336–441 (ang.).
- ↑ Finkelstein J., One-way speed of light?, „American Journal of Physics”, 8, 78, 2009, s. 877, DOI: 10.1119/1.3364868, Bibcode: 2009arXiv0911.3616F, arXiv:0911.3616 (ang.).
- ↑ Md.F. Ahmed i inni, A Review of One-Way and Two-Way Experiments to Test the Isotropy of the Speed of Light, „Indian Journal of Physics”, 86 (9), 2012, s. 835–848, DOI: 10.1007/s12648-012-0112-4, Bibcode: 2012InJPh..86..835A, arXiv:1011.1318v2 (ang.).
- ↑ Schleif Roberts, Relativity FAQ – One-Way Tests of Light-Speed Isotropy [online], 2006 (ang.).
- ↑ Timothy P. Krisher i inni, Test of the isotropy of the one-way speed of light using hydrogen-maser frequency standards, „Physical Review D”, 42 (2), 1990, s. 731–734, DOI: 10.1103/PhysRevD.42.731, Bibcode: 1990PhRvD..42..731K (ang.).
- ↑ Zhang 1997 ↓, s. 148–150.
- ↑ Zhang 1997 ↓, s. 91–94.
- ↑ Karlov L. Does Romer’s method yield a unidirectional speed of light?. „Australian Journal of Physics”. 23, s. 243–253, 1970. DOI: 10.1071/PH700243. Bibcode: 1970AuJPh..23..243K. (ang.).
- ↑ V.N. Matveev, O.V. Matvejev, Simulation of Kinematics of Special Theory of Relativity, „arXiv.org”, arXiv:1201.1828 [physics.gen-ph] (ang.).
- ↑ R.F.C. Vessot i inni, Test of relativistic gravitation with a space-borne hydrogen maser, „Physical Review Letters”, 45 (29), 1980, s. 2081–2084, DOI: 10.1103/PhysRevLett.45.2081, Bibcode: 1980PhRvL..45.2081V (ang.).
- ↑ Erling Riis i inni, Test of the Isotropy of the speed of light using fast-beam laser spectroscopy, „Physical Review Letters”, 60 (11), 1988, s. 81–84, DOI: 10.1103/PhysRevLett.60.81, Bibcode: 1988PhRvL..60...81R (ang.).
- ↑ Nelson R.A. i inni, Experimental comparison of time synchronization techniques by means of light signals and clock transport on the rotating earth, „Proceedings of the 24th PTTI meeting”, 24, 1992, s. 87–104 [dostęp 2018-11-10] [zarchiwizowane z adresu 2017-02-23] (ang.).
- ↑ Wolf Peter, Petit Gérard. Satellite test of special relativity using the global positioning system. „Physical Review A”. 56 (6), s. 4405–4409, 1997. DOI: 10.1103/PhysRevA.56.4405. Bibcode: 1997PhRvA..56.4405W. (ang.).
- ↑ Brecher K., Is the speed of light independent of the velocity of the source, „Physical Review Letters”, 17, 39, 1977, s. 1051–1054, DOI: 10.1103/PhysRevLett.39.1051, Bibcode: 1977PhRvL..39.1051B (ang.).
- ↑ Alväger T., Nilsson A., Kjellman J., A Direct Terrestrial Test of the Second Postulate of Special Relativity, „Nature”, 197 (4873), 1963, s. 1191, DOI: 10.1038/1971191a0, Bibcode: 1963Natur.197.1191A (ang.).
- ↑ Giovanni Amelino-Camelia, Astrophysics: Burst of support for relativity, „Nature”, 462 (7271), 2009, s. 291–292, DOI: 10.1038/462291a, PMID: 19924200, Bibcode: 2009Natur.462..291A (ang.).
- ↑ a b c d Kostelecký V. Alan, Mewes, Matthew. Signals for Lorentz violation in electrodynamics. „Physical Review D”. 66 (5), s. 056005, 2002. DOI: 10.1103/PhysRevD.66.056005. arXiv:hep-ph/0205211. Bibcode: 2002PhRvD..66e6005K. (ang.).
- ↑ a b Edwards W.F. Special Relativity in Anisotropic Space. „American Journal of Physics”. 31 (7), s. 482–489, 1963. DOI: 10.1119/1.1969607. Bibcode: 1963AmJPh..31..482E. (ang.).
Bibliografia[edytuj | edytuj kod]
- Yuan-Zhong Zhang, Special Relativity and Its Experimental Foundations, World Scientific, 1997, ISBN 978-981-02-2749-4 [dostęp 2017-09-29] [zarchiwizowane z adresu 2012-05-19].
Linki zewnętrzne[edytuj | edytuj kod]
 Why No One Has Measured The Speed Of Light, kanał Veritasium na YouTube, 31 października 2020 [dostęp 2024-02-14].
Why No One Has Measured The Speed Of Light, kanał Veritasium na YouTube, 31 października 2020 [dostęp 2024-02-14].- Mathpages: Conventional Wisdom, Round Trips and One-Way Speeds, Teaching Special Relativity
- Allen Janis, Conventionality of Simultaneity, [w:] Stanford Encyclopedia of Philosophy, CSLI, Stanford University, 21 lipca 2018, ISSN 1095-5054 [dostęp 2018-08-03] (ang.).
- Rizzi, Guido, Ruggiero, Matteo Luca, Serafini, Alessio. Synchronization Gauges and the Principles of Special Relativity. „Foundations of Physics”. 34 (12), s. 1835–1887, 2004. DOI: 10.1007/s10701-004-1624-3. arXiv:gr-qc/0409105. Bibcode: 2004FoPh...34.1835R.
- Sonego, Sebastiano, Pin, Massimo. Foundations of anisotropic relativistic mechanics. „Journal of Mathematical Physics”. 50 (4), s. 042902–042901–042902–28, 2008. DOI: 10.1063/1.3104065. arXiv:0812.1294. Bibcode: 2009JMP....50d2902S.





















![{\displaystyle {\begin{aligned}d{\tilde {t}}'&={\tilde {\gamma }}\left[1+\kappa \cdot {\tilde {\mathbf {v} }}/c-\kappa '\cdot {\tilde {\mathbf {v} }}'/c\right]d{\tilde {t}}-\left(\kappa '+{\tilde {\gamma }}{\tilde {\mathbf {v} }}'\right)\cdot d{\tilde {\mathbf {x} }}/c\\&\;\;\;-\left[{\tilde {\gamma }}\left(1+\kappa \cdot {\tilde {\mathbf {v} }}/c\right)-1\right]{\frac {\kappa '\cdot {\tilde {\mathbf {v} }}}{{\tilde {\mathbf {v} }}^{2}c}}{\tilde {\mathbf {v} }}\cdot d{\tilde {\mathbf {x} }}+{\tilde {\gamma }}\kappa \cdot {\tilde {\mathbf {v} }}\left(\kappa \cdot d{\tilde {\mathbf {x} }}\right)/c,\\d{\tilde {\mathbf {x} }}'&=-{\tilde {\gamma }}{\tilde {\mathbf {v} }}d{\tilde {t}}+d{\tilde {\mathbf {x} }}+\left[{\tilde {\gamma }}\left(1+\kappa \cdot {\tilde {\mathbf {v} }}/c\right)-1\right]{\frac {{\tilde {\mathbf {v} }}\cdot d\mathbf {x} }{{\tilde {\mathbf {v} }}^{2}}}{\tilde {\mathbf {v} }}-{\tilde {\gamma }}{\tilde {\mathbf {v} }}\left(\kappa \cdot d{\tilde {\mathbf {x} }}\right)/c,\\{\tilde {\gamma }}&=\gamma \left(1-\kappa \cdot \mathbf {v} /c\right),\\{\tilde {\mathbf {v} }}&={\frac {\mathbf {v} }{1-\kappa \cdot \mathbf {v} /c}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7756028b920d7315f0060860365887e7fb691ec)

