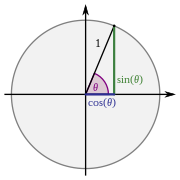
Tożsamości trygonometryczne – podstawowe zależności pomiędzy funkcjami trygonometrycznymi.
Wzór

jest prawdziwy dla dowolnej liczby rzeczywistej (a nawet zespolonej, przy przyjęciu ogólniejszych definicji). Tożsamość ta uznawana jest za podstawową tożsamość trygonometryczną. Zwana często jedynką trygonometryczną bądź trygonometrycznym twierdzeniem Pitagorasa.
Istnieją również dwie inne wariacje tego wzoru:


Funkcje trygonometryczne są okresowe 











Równości
![{\displaystyle {\begin{aligned}&\sin x=\cos \left({\frac {\pi }{2}}-x\right)&&\cos x=\sin \left({\frac {\pi }{2}}-x\right)\\[.2em]&\operatorname {tg} x=\operatorname {ctg} \left({\frac {\pi }{2}}-x\right)&&\operatorname {ctg} x=\operatorname {tg} \left({\frac {\pi }{2}}-x\right)\\[.2em]&\sec x=\operatorname {cosec} \left({\frac {\pi }{2}}-x\right)&&\operatorname {cosec} x=\sec \left({\frac {\pi }{2}}-x\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd95bdb88e651940e908933f83dcad199334479)
nazywa się związkami pomiędzy funkcjami a ich kofunkcjami. Kofunkcją sinusa jest cosinus, cosinusa sinus, tangensa cotangens itd.
Funkcje trygonometryczne można układać w pary według kofunkcji lub według odwrotności. Odwrotnością sinusa jest cosecans, cosinusa secans, tangensa cotangens (i oczywiście na odwrót):
![{\displaystyle {\begin{aligned}&\sin x={\frac {1}{\operatorname {cosec} x}}&&\operatorname {cosec} x={\frac {1}{\sin x}}\\[.5em]&\cos x={\frac {1}{\sec x}}&&\sec x={\frac {1}{\cos x}}\\[.5em]&\operatorname {tg} x={\frac {1}{\operatorname {ctg} x}}&&\operatorname {ctg} x={\frac {1}{\operatorname {tg} x}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c997a622134bd906219470948bb3121aa2633ce5)




Wzory na dwukrotność kąta otrzymuje się przez podstawienie  we wzorach na funkcje sumy kątów.
we wzorach na funkcje sumy kątów.












Ogólnie:
![{\displaystyle {\begin{aligned}\sin nx&=\sum _{i=0}^{\infty }(-1)^{i}\cdot {n \choose 2i+1}\cos ^{n-2i-1}x\sin ^{2i+1}x\\[2pt]&=\sum _{i=0}^{\lfloor {\frac {n}{2}}\rfloor }(-1)^{i}\cdot {n \choose 2i+1}\cos ^{n-2i-1}x\sin ^{2i+1}x\\&=n\cos ^{n-1}x\sin x-{n \choose 3}\cos ^{n-3}x\sin ^{3}x+{n \choose 5}\cos ^{n-5}x\sin ^{5}x-{n \choose 7}\cos ^{n-7}x\sin ^{7}x+\dots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/714e1218d101c47c2664961856dd7d3326ba7738)
![{\displaystyle {\begin{aligned}\cos nx&=\sum _{i=0}^{\infty }(-1)^{i}\cdot {n \choose 2i}\cos ^{n-2i}x\sin ^{2i}x\\[2pt]&=\sum _{i=0}^{\lfloor {\frac {n}{2}}\rfloor }(-1)^{i}\cdot {n \choose 2i}\cos ^{n-2i}x\sin ^{2i}x\\&=\cos ^{n}x-{n \choose 2}\cos ^{n-2}x\sin ^{2}x+{n \choose 4}\cos ^{n-4}x\sin ^{4}x-{n \choose 6}\cos ^{n-6}x\sin ^{6}x+\dots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eb40d217ed38a880497203d0468cb9a544202f5)

































Funkcje trygonometryczne wyrażone przy pomocy tangensa połowy kąta
[edytuj | edytuj kod]


Powyższe tożsamości znalazły zastosowanie w tzw. podstawieniu uniwersalnym, stosowanym przy obliczaniu całek typu  gdzie
gdzie  jest funkcją wymierną zmiennych
jest funkcją wymierną zmiennych  Stosuje się podstawienie:
Stosuje się podstawienie:



 Osobny artykuł: Wzór Eulera.
Osobny artykuł: Wzór Eulera.




Wzory te pozwalają łatwo przekształcać wyrażenia trygonometryczne, poprzez przejście na postać zespoloną (cztery ostatnie wzory), uproszczenie i powrót na postać trygonometryczną (pierwszy wzór).

Wzór de Moivre’a

lub ogólniej:
![{\displaystyle [r(\cos x+i\sin x)]^{n}=r^{n}(\cos nx+i\sin nx)\qquad n\in \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/76357c43423817aec6638c42c3dfecbcfbbcfde5)
 Paweł Lubowiecki, Funkcje trygonometryczne cz. IV Tożsamości trygonometryczne, Wojskowa Akademia Techniczna im. Jarosława Dąbrowskiego, kanał „Uczelnia WAT” na YouTube, 30 stycznia 2024 [dostęp 2024-09-07].
Paweł Lubowiecki, Funkcje trygonometryczne cz. IV Tożsamości trygonometryczne, Wojskowa Akademia Techniczna im. Jarosława Dąbrowskiego, kanał „Uczelnia WAT” na YouTube, 30 stycznia 2024 [dostęp 2024-09-07].















![{\displaystyle {\begin{aligned}&\sin x=\cos \left({\frac {\pi }{2}}-x\right)&&\cos x=\sin \left({\frac {\pi }{2}}-x\right)\\[.2em]&\operatorname {tg} x=\operatorname {ctg} \left({\frac {\pi }{2}}-x\right)&&\operatorname {ctg} x=\operatorname {tg} \left({\frac {\pi }{2}}-x\right)\\[.2em]&\sec x=\operatorname {cosec} \left({\frac {\pi }{2}}-x\right)&&\operatorname {cosec} x=\sec \left({\frac {\pi }{2}}-x\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd95bdb88e651940e908933f83dcad199334479)
![{\displaystyle {\begin{aligned}&\sin x={\frac {1}{\operatorname {cosec} x}}&&\operatorname {cosec} x={\frac {1}{\sin x}}\\[.5em]&\cos x={\frac {1}{\sec x}}&&\sec x={\frac {1}{\cos x}}\\[.5em]&\operatorname {tg} x={\frac {1}{\operatorname {ctg} x}}&&\operatorname {ctg} x={\frac {1}{\operatorname {tg} x}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c997a622134bd906219470948bb3121aa2633ce5)




















![{\displaystyle {\begin{aligned}\sin nx&=\sum _{i=0}^{\infty }(-1)^{i}\cdot {n \choose 2i+1}\cos ^{n-2i-1}x\sin ^{2i+1}x\\[2pt]&=\sum _{i=0}^{\lfloor {\frac {n}{2}}\rfloor }(-1)^{i}\cdot {n \choose 2i+1}\cos ^{n-2i-1}x\sin ^{2i+1}x\\&=n\cos ^{n-1}x\sin x-{n \choose 3}\cos ^{n-3}x\sin ^{3}x+{n \choose 5}\cos ^{n-5}x\sin ^{5}x-{n \choose 7}\cos ^{n-7}x\sin ^{7}x+\dots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/714e1218d101c47c2664961856dd7d3326ba7738)
![{\displaystyle {\begin{aligned}\cos nx&=\sum _{i=0}^{\infty }(-1)^{i}\cdot {n \choose 2i}\cos ^{n-2i}x\sin ^{2i}x\\[2pt]&=\sum _{i=0}^{\lfloor {\frac {n}{2}}\rfloor }(-1)^{i}\cdot {n \choose 2i}\cos ^{n-2i}x\sin ^{2i}x\\&=\cos ^{n}x-{n \choose 2}\cos ^{n-2}x\sin ^{2}x+{n \choose 4}\cos ^{n-4}x\sin ^{4}x-{n \choose 6}\cos ^{n-6}x\sin ^{6}x+\dots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eb40d217ed38a880497203d0468cb9a544202f5)

















































![{\displaystyle [r(\cos x+i\sin x)]^{n}=r^{n}(\cos nx+i\sin nx)\qquad n\in \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/76357c43423817aec6638c42c3dfecbcfbbcfde5)