Trygonometria

Wszystkie funkcje trygonometryczne kąta θ mogą zostać geometrycznie skonstruowane w odniesieniu do okręgu ze środkiem w punkcie O

Trygonometria (łac. trigonometria) – dział matematyki z pogranicza geometrii płaskiej i analizy, badający:

• związki miarowe między bokami i kątami trójkątów;
• funkcje trygonometryczne, początkowo definiowane przez trójkąty, a później też w inny sposób; badania te bywają nazywane goniometrią, przy czym termin ten ma też inne znaczenia.

Trygonometria bada zarówno trójkąty na płaszczyźnie, jak i te sferyczne, przez co wyróżnia się trygonometrię płaską i sferyczną.

Nauka ta istnieje od starożytności. Rozwijali ją uczeni starogreccy, islamscy oraz średniowiecznej i nowożytnej Europy, m.in. na potrzeby astronomii. Stała się standardowym elementem kursów matematyki w szkołach średnich; przykładowo należy do podstawy programowej polskich liceów i techników, także w zakresie podstawowym.

Historia

Ogólny zarys

Trygonometria powstała najpóźniej w starożytnej Grecji w okresie hellenistycznym na potrzeby geodezji, astronomii i ich zastosowań do nawigacji, np. żeglugi. Stosunki boków w trójkątach badali także matematycy indyjscy oraz kontynuujący ich prace uczeni chińscy i islamscy, którzy zaprowadzili te wyniki do Europy. Tam nazwano tę dyscyplinę, podano wykresy funkcji trygonometrycznych, zdefiniowano je dla dowolnych argumentów rzeczywistych oraz opracowano szeregi pozwalające obliczać wartości tych funkcji bez fizycznego pomiaru trójkątów. W XVIII wieku udało się też sprowadzić funkcje trygonometryczne do nieskończonych iloczynów, ułamków łańcuchowych oraz powiązać je z funkcją wykładniczą za pomocą wzoru Eulera. Rozwój trygonometrii został w ten sposób ukoronowany, jednak później znajdowano dla niej coraz nowsze zastosowania; przykładowo w XIX wieku powstała analiza harmoniczna.

Rola trygonometrii nie ogranicza się do praktycznego przewidywania odległości i miar kątów:

• tożsamości trygonometryczne znalazły zastosowania w algebrze, np. jako uzupełnienie wzorów Cardana na pierwiastki równania kubicznego;
• z trygonometrii skorzystała też teoria liczb; w XVIII wieku Johann Heinrich Lambert za pomocą jednego ze wzorów na funkcję tangens udowodnił, że liczba pi (π) jest niewymierna. W XIX i XX wieku podano nowe wzory na tę stałą zawierające funkcje cyklometryczne; obliczanie jej coraz szybciej i z rosnącą precyzją ma pewne znaczenie teoretyczne, np. pozwala sprawdzać pewne hipotezy na jej temat.

Egipt i Babilon

Tabliczka Plimpton 322

W starożytnym Egipcie i Babilonie od wieków znano twierdzenia dotyczące stosunków boków trójkątów podobnych. Jednak społeczeństwa przed Grekami prawdopodobnie nie wynalazły idei miary kąta i w konsekwencji badały tylko boki trójkąta.

Niektórzy badacze uważają, że starożytni Babilończycy zapisali pismem klinowym na tabliczce Plimpton 322, powstałej ok. 1800–1900 lat p.n.e., tablicę sekansów. Jednakże według innych interpretacji mogły to być tablice trójek pitagorejskich albo rozwiązanie równania kwadratowego.

Starożytna Grecja

Cięciwa łuku utworzonego przez dany kąt

Średniowieczne przedstawienie Klaudiusza Ptolemeusza

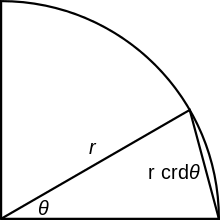
Matematycy starożytnej Grecji znali pojęcie cięciwy. Dla danego okręgu i jego części (łuku) cięciwa jest prostą, która przecina okrąg na końcach łuku. Symetralna odcinka cięciwy mieszczącego się wewnątrz koła przechodzi przez jego środek i dzieli łuk (i tym samym kąt) na pół. Połowa długości cięciwy to dla okręgu jednostkowego sinus połowy kąta, czyli ${\mbox{crd}}\ \theta =2\sin {\tfrac {\theta }{2}}.$ Wiele z twierdzeń trygonometrycznych było znanych starożytnym Grekom, jednak w postaci odpowiedników operujących długościami łuków i cięciw, a nie miarami kątów i stosunkami długości boków trójkąta.

Jakkolwiek w dziełach Euklidesa i Archimedesa nie było trygonometrii w ścisłym tego słowa znaczeniu, są jednak twierdzenia zaprezentowane w geometrycznej formie, które stanowią odpowiedniki pewnych trygonometrycznych praw i wzorów. Na przykład propozycje XII i XIII z Księgi II Elementów są tożsame ze wzorem cosinusów odpowiednio dla kątów rozwartych i ostrych. Twierdzenia dotyczące długości cięciw są natomiast zastosowaniem wzoru sinusów. Jedno z twierdzeń Archimedesa jest zaś odpowiednikiem wzoru na sinus sumy i różnicy kątów. Matematycy za czasów Arystarcha z Samos dla celów obliczeniowych używali m.in. twierdzenia mówiącego, iż (we współczesnej notacji) ${\tfrac {\sin \alpha }{\sin \beta }}<{\tfrac {\alpha }{\beta }}<{\tfrac {\operatorname {tg} \alpha }{\operatorname {tg} \beta }}$ dla $0^{\circ }<\beta <\alpha <90^{\circ }$.

Pierwsze tablice trygonometryczne zostały prawdopodobnie skompilowane przez Hipparcha (180–125 p.n.e.). Hipparch jako pierwszy ułożył tablice odpowiadających sobie długości cięciwy i łuku dla różnych kątów.

Jakkolwiek nie wiadomo dokładnie, kiedy zaczęto używać podziału kąta pełnego na 360 stopni, przypuszczalnie nastąpiło to wkrótce po napisaniu przez Arystarcha z Samos dzieła O rozmiarach i odległościach Słońca i Księżyca ok. 260 p.n.e., gdyż mierzył on kąty w ułamkach kąta prostego. Prawdopodobnie podział kąta pełnego na 360 stopni spopularyzował się głównie dzięki Hipparchowi i jego tablicy cięciw. Hipparch mógł podchwycić ideę takiego podziału u Hipsikla, który wcześniej dzielił dobę na 360 części, zapewne wzorując się na babilońskich astronomach. W starożytnej astronomii ekliptyka została podzielona na 12 „znaków zodiaku” lub 36 dekanów. Roczny cykl około 360 dni można było otrzymać, dzieląc każdy znak na 30 części i każdy dekan na 10 części. To dzięki używanemu w Babilonii sześćdziesiątkowemu systemowi liczbowemu każdy stopień został podzielony na 60 minut kątowych, a każda minuta na 60 sekund kątowych.

Menelaos z Aleksandrii (ok. 100 n.e.) napisał trzy księgi pod tytułem Sphaerica. W Księdze I sformułował dla trójkątów sferycznych odpowiedniki twierdzeń dotyczących trójkątów na płaszczyźnie. Sformułował również twierdzenie nieposiadające odpowiednika na płaszczyźnie euklidesowej, mówiące, że dwa trójkąty sferyczne są przystające, jeśli odpowiednie ich kąty mają równe miary (utożsamiał przy tym symetryczne wersje trójkątów sferycznych). Menelaos zauważył także, że suma kątów wewnętrznych trójkąta sferycznego jest zawsze większa od 180°. Księga II Sphaerica dotyczyła zastosowań geometrii sferycznej do astronomii. Księga III zawierała „twierdzenie Menelausa”.

Później Klaudiusz Ptolemeusz (ok. 90 – ok. 168 n.e.) rozbudował w swoim dziele Almagest koncepcję „cięciw na okręgu” Hipparcha. Trzynasta księga Almagestu była znaczącą starożytną pracą w dziedzinie trygonometrii. Jedno z jej twierdzeń jest dziś znane jako twierdzenie Ptolemeusza. Szczególny przypadek twierdzenia Ptolemeusza pojawia się także w Propozycji XCIII dzieła Euklidesa. Twierdzenie Ptolemeusza prowadzi do równoważnika wzorów na sinus i cosinus sumy i różnicy, choć oczywiście wyrażonych w języku cięciw, a nie funkcji. Ptolemeusz wyprowadził później ekwiwalent wzoru

$\sin ^{2}{\tfrac {x}{2}}={\tfrac {1-\cos x}{2}}.$

Ptolemeusz używał tych wyników do stworzenia tablic trygonometrycznych, choć nie wiadomo, czy nie były one wyprowadzone z dzieła Hipparcha.

Ani tablice Hipparcha, ani Ptolemeusza nie przetrwały do czasów współczesnych, choć dzięki wzmiankom u innych autorów nie ma wątpliwości, że istniały.

Średniowieczne Indie

Posąg Aryabhaty

Kolejny istotny postęp w trygonometrii został dokonany w Indiach. Indyjski matematyk i astronom Aryabhata (476–550 n.e.) w swoim dziele Aryabhata-Siddhanta po raz pierwszy zdefiniował sinus w znanej dzisiaj formie związku między połową kąta i połową cięciwy, a także cosinus, sinus versus i arcus sinus. Jego dzieła zawierają najwcześniejsze tablice trygonometryczne, które przetrwały do dzisiaj, z wartościami funkcji sinus i sinus versus co 3.75° stopnia od 0° do 90°, z dokładnością do czterech miejsc znaczących. Jego nazwy na sinus i cosinus stały się podstawą nazw używanych dzisiaj (zobacz Definicja na okręgu jednostkowym i etymologia nazw funkcji trygonometrycznych).

Inni hinduscy matematycy rozwinęli później pracę Aryabhaty. W VI wieku n.e. Varahamihira używał wzorów:

$\sin ^{2}x+\cos ^{2}x=1,$

$\sin x=\cos \left({\tfrac {\pi }{2}}-x\right),$

${\tfrac {1-\cos(2x)}{2}}=\sin ^{2}x.$

W VII wieku Bhaskara I stworzył wzór pozwalający na przybliżone obliczanie sinusa dla kąta ostrego bez tablic (z błędem mniejszym od 1,9%):

$\sin x\approx {\tfrac {16x(\pi -x)}{5\pi ^{2}-4x(\pi -x)}},\qquad 0\leqslant x\leqslant {\tfrac {\pi }{2}}.$

W końcu VII wieku, Brahmagupta wyprowadził wzór:

$1-\sin ^{2}x=\cos ^{2}x=\sin ^{2}\left({\tfrac {\pi }{2}}-x\right)$

oraz tzw. wzór interpolacyjny Brahmagupty:

$f(a+xh)\approx f(a)+x\left({\tfrac {\Delta f(a)+\Delta f(a-h)}{2}}\right)+{\tfrac {x^{2}\Delta ^{2}f(a-h)}{2}},$

który pozwolił mu na stablicowanie wartości sinusa.

Świat islamu

Al-Chuwarizmi sportretowany na radzieckim znaczku pocztowym

Prace matematyków hinduskich zostały później przetłumaczone i rozszerzone w świecie muzułmańskim przez arabskich i perskich matematyków. W IX wieku Muhammad ibn Musa al-Chuwarizmi obliczył dokładne tablice sinusa i cosinusa i pierwsze w historii tablice tangensa.

W X wieku islamscy matematycy używali wszystkich sześciu funkcji trygonometrycznych z secansem i cosecansem włącznie, co wiadomo dzięki pracy autorstwa Abu al-Wafa. Abu al-Wafa stworzył tablice sinusa z krokiem 0,25° i dokładnością 8 cyfr dziesiętnych, a także dokładne tablice tangensa. Zauważył również tożsamość:

$\sin 2x=2\sin x\cos x.$

Wszystkie te wczesne wyniki trygonometryczne powstawały głównie w związku z pracami astronomicznymi, pierwsze traktaty wyłącznie o trygonometrii opublikowali zapewne Bhāskara Acārya i Nasir ad-Din Tusi w XIII wieku. Nasir ad-Din Tusi sformułował i udowodnił twierdzenie sinusów, sklasyfikował też sześć różnych przypadków prostokątnych trójkątów sferycznych.

W XIV wieku Ghijas ad-Din Kaszi stworzył tablice sinusa z dokładnością do czterech cyfr sześćdziesiątkowych (odpowiednik 8 miejsc dziesiętnych) dla każdego stopnia z dodatkowymi poprawkami do obliczania wartości dla każdej minuty kątowej. Uług Beg (XV wiek) także podał dokładne tablice sinusa i tangensa sięgające 8 miejsc dziesiętnych.

Średniowieczne Chiny

Guo Shoujing (1231–1316)

Tablice sinusów Aryabhaty zostały przetłumaczone na chiński i umieszczone w klasycznym dziele Kaiyuan Zhan Jing, skompilowanym w 718 roku w okresie dynastii Tang. Jakkolwiek Chińczycy celowali w innych dziedzinach matematyki, takich jak stereometria, czy algebra, to wczesne formy trygonometrii nie rozpowszechniły się tak szybko jak w przypadku Greków, Hindusów i muzułmanów. Powoli ten stan zaczął się zmieniać w okresie dynastii Song (960–1279), kiedy chińscy matematycy zaczęli kłaść większy nacisk na potrzeby geometrii sferycznej. Na przykład Shen Kuo (1031–1095) używał funkcji trygonometrycznych do rozwiązywania problemów matematycznych z cięciwami i łukami. Jak twierdzą historycy L. Gauchet i Joseph Needham, inny matematyk, Guo Shoujing (1231–1316) używał trygonometrii sferycznej w kalkulacjach kalendarzowych i astronomicznych.

Renesansowa Europa

Regiomontanus był prawdopodobnie pierwszym europejskim matematykiem, który traktował trygonometrię jako oddzielną dyscyplinę matematyczną. Napisał w 1464 De triangulis omnimodus, a później Tabulae directionum.

Funkcję secans w Europie wprowadził Mikołaj Kopernik w dziele De revolutionibus orbium coelestium (1543), choć arabscy matematycy używali jej prawdopodobnie już w IX wieku.

Francesco Maurolico w 1555 używał zapisu sinus, w 1583 J. Finck użył określeń tangens oraz sekans. Edmund Gunter w 1620 roku użył słowa cotangens, w 1624 roku wprowadził oznaczenie sin x oraz tan x, a w 1636 cosi x oraz słowo cosinus (zamiast complementi sinus). François Viète w 1590 znalazł wzór na $\cos nx$.

W 1595 Bartłomiej Pitiscus użył po raz pierwszy terminu „trygonometria” w swoim dziele Trigonometria: sive de solutione triangulorum Tractatus brevis et perspicuus (1595, Heidelberg).

Opus palatinum de triangulis autorstwa Retyka, było prawdopodobnie pierwszą definicją funkcji trygonometrycznych w terminach trójkątów prostokątnych zamiast okręgów jednostkowych; ta praca została dokończona przez Valentina Otho, studenta Rheticusa w roku 1596.

Isaac Newton w 1665 znalazł rozwinięcie funkcji sinus i cosinus w szereg, a Leonhard Euler w 1734 rozwinięcie funkcji sinus w iloczyn nieskończony.

W XVII wieku Isaac Newton i James Stirling stworzyli wzór interpolacyjny Newtona-Stirlinga dla funkcji trygonometrycznych.

W 1770 Johann Heinrich Lambert znalazł reprezentację tangensa w postaci ułamka łańcuchowego.

Historia analizy trygonometrycznej

Leonhard Euler (1707–1783) – szwajcarski matematyk, który udowodnił pewne własności funkcji trygonometrycznych, m.in. ich związek z funkcją wykładniczą nazywany wzorem Eulera.

Madhava (około roku 1400) stworzył podwaliny analizy matematycznej funkcji trygonometrycznych, odkrywając rozwinięcie funkcji w szeregi nieskończone. Badał on koncepcje szeregów potęgowych oraz pewnego szeregu, nazwanego później w Europie szeregiem Taylora i obliczył rozwinięcia sinusa, cosinusa, tangensa i cotangensa. Używając aproksymacji sinusa i cosinusa szeregiem Taylora, stworzył tablice sinusa z 12 miejscami znaczącymi i cosinusa z 9 miejscami znaczącymi. Podał także rozwinięcie π w szereg potęgowy. Jego prace były rozwijane przez jego następców ze szkoły astronomicznej w Kerala aż do XVI wieku.

Introductio in analysin infinitorum Leonharda Eulera z 1748 roku stworzyło grunt dla analitycznego traktowania funkcji trygonometrycznych w Europie, definiując je jako nieskończone szeregi i wprowadzając „wzór Eulera”. Euler używał skrótów zbliżonych do dzisiejszych: sin., cos., tang., cot., sec., i cosec.

James Gregory, a następnie Brook Taylor badali szeregi, znane dziś jako szeregi Taylora. Ten ostatni znalazł rozwinięcia i aproksymacje wszystkich sześciu funkcji trygonometrycznych. Duże znaczenie na tym polu miały również prace Colina Maclaurina.

Zobacz też

• równanie trygonometryczne
• trygonometryczne wzory redukcyjne
• twierdzenie cosinusów, twierdzenie tangensów – twierdzenia przydatne przy rozwiązywaniu zadań dotyczących trójkątów

Bibliografia

• Carl B. Boyer: A History of Mathematics. Wyd. Second Edition. John Wiley & Sons, Inc., 1991. ISBN 0-471-54397-7.
• J.J. O’Connor, E.F. Robertson: Madhava of Sangamagramma. [w:] MacTutor History of Mathematics Archive [on-line]. 2000. (ang.).
• J.J. O’Connor, E.F. Robertson: Trigonometric functions. [w:] MacTutor History of Mathematics Archive [on-line]. 1996. (ang.).
• L. Gauchet: Note Sur La Trigonométrie Sphérique de Kouo Cheou-King. 1917.
• George G. Joseph: The Crest of the Peacock: Non-European Roots of Mathematics. Wyd. 2. Londyn: Penguin Books, 2000. ISBN 0-691-00659-8.
• Joseph Needham: Science and Civilization in China: tom 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd., 1986.
• Ian G. Pearce: Madhava of Sangamagramma. [w:] MacTutor History of Mathematics Archive [on-line]. 2002. [dostęp 2009-03-24]. [zarchiwizowane z tego adresu (2006-05-05)]. (ang.).
• R.P. Kostecki: Krótka historia matematyki

Linki zewnętrzne

• Geometria – trygonometria, Khan Academy, kanał „KhanAcademyPoPolsku” na YouTube [dostęp 2025-10-28].
• Eric W.E.W. Weisstein Eric W.E.W., Trigonometry, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2023-06-01].