Rozkład Pareto

Rozkład Pareto

Gęstość prawdopodobieństwa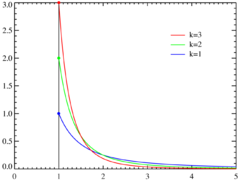 Gęstość prawdopodobieństwa rozkładu Pareto dla różnych k  oraz xm = 1. Oś odciętych odpowiada parametrowi x. Dla k dążącego do nieskończoności rozkład zbiega do δ(x − xm) gdzie δ to delta Diraca.
Dystrybuanta Dystrybuanta rozkładu Pareto dla różnych k  oraz xm = 1. Oś odciętych odpowiada parametrowi x.
Parametry	$x_\mathrm{m}>0\,$ parametr skali (liczba rzeczywista) $k>0\,$ parametr kształtu (liczba rzeczywista)
Nośnik	$x \in [x_\mathrm{m}; +\infty)\!$
Gęstość prawdopodobieństwa	$\frac{k\,x_\mathrm{m}^k}{x^{k+1}}\!$
Dystrybuanta	$1-\left(\frac{x_\mathrm{m}}{x}\right)^k\!$
Wartość oczekiwana (średnia)	$\frac{k\,x_\mathrm{m}}{k-1}\!$ dla $k>1$
Mediana	$x_\mathrm{m} \sqrt[k]{2}$
Moda	$x_\mathrm{m}\,$
Wariancja	$\frac{x_\mathrm{m}^2k}{(k-1)^2(k-2)}\!$ dla $k>2$
Współczynnik skośności	$\frac{2(1+k)}{k-3}\,\sqrt{\frac{k-2}{k}}\!$ dla $k>3$
Kurtoza	$\frac{6(k^3+k^2-6k-2)}{k(k-3)(k-4)}\!$ dla $k>4$
Entropia	$\ln\left(\frac{k}{x_\mathrm{m}}\right) - \frac{1}{k} - 1\!$
Funkcja generująca momenty	nieokreślona
Funkcja charakterystyczna	$k(-ix_\mathrm{m}t)^k\Gamma(-k,-ix_\mathrm{m}t)\,$
Odkrywca	Vilfredo Pareto

Rozkład Pareto, od nazwiska włoskiego ekonomisty Vilfredo Pareto, jest ciągłym rozkładem prawdopodobieństwa, spełniającym potęgowe prawo skalowania, występującym m.in. w naukach społecznych, geofizyce, i aktuariacie. Poza ekonomią jest czasem nazywany rozkładem Bradforda.

Pareto oryginalnie używał tego rozkładu do opisu alokacji dóbr w społeczeństwie, gdyż jak zauważył większa część bogactwa dowolnego społeczeństwa jest w posiadaniu niewielkiego procenta jego członków.

Idea ta jest czasem wyrażana jako tzw. zasada Pareto, mówiąca, że 20% populacji posiada 80% bogactwa. Konkretne wartości mogą być jednak inne w zależności od parametrów rozkładu.

Rozkład Pareto występuje też w wielu innych sytuacjach, w szczególności:

• Częstości występowania słów w długich tekstach (kilka słów jest używanych często, wiele słów rzadko).
• Rozmiary osiedli ludzkich (mało dużych miast, dużo małych wsi)
• Wielkości plików przesyłanych protokołem TCP w internecie (dużo małych plików, mało dużych plików).
• Klastry kondensatu Bosego-Einsteina w okolicach zera Kelwina.
• Pojemność złóż ropy naftowej (mało dużych pól naftowych, dużo małych pól)
• Czas wykonywania procesu obliczeniowego przez superkomputer (niewiele długich procesów, dużo krótkich)
• Rozmiar ziarenek piasku
• Rozmiar meteorytów
• Liczba gatunków w rodzaju (intuicyjnie: Im większy rodzaj, tym większa skłonność badaczy do podzielenia go na dwa mniejsze dla lepszego oddania indywidualnych cech zawierających się w nim gatunków)
• Powierzchnia spalona podczas pożaru lasu
• Rozmiar finansowej odpowiedzialności ubezpieczyciela w związku z wypadkami losowymi jego klientów przy ubezpieczeniu OC, AC oraz od wypadków przy pracy.

Zobacz też

• zasada Pareto