Deltoid

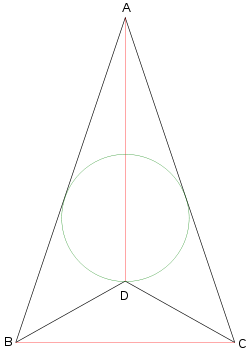
Deltoid – czworokąt mający oś symetrii, która przechodzi przez dwa jego wierzchołki. Oś symetrii zawiera przekątną łączącą te wierzchołki i jednocześnie jest symetralną drugiej przekątnej. Wśród czterech boków deltoidu są dwie pary sąsiednich boków o tej samej długości.
Niektórzy autorzy żądają też, aby deltoid był wypukły[1][2]. Według niektórych, np. Jana Zydlera[3] deltoid dodatkowo nie może mieć wszystkich boków równych[4]. Większość źródeł nie tworzy jednak takich wyjątków i uważa romb za szczególny przypadek deltoidu[2][5][6][7].
Własności[edytuj | edytuj kod]
W deltoidzie kąty między bokami różnej długości są równe. Każdy deltoid wypukły jest sumą (mnogościową) dwóch trójkątów równoramiennych. W deltoid wypukły można wpisać okrąg.
Pole powierzchni deltoidu jest połową iloczynu długości jego przekątnych[8]. Jest także równe iloczynowi długości dwóch sąsiednich boków deltoidu o różnych długościach i sinusa kąta między nimi:
Przypisy[edytuj | edytuj kod]
- ↑ Matematyka, Warszawa: Wydawnictwa Szkolne i Pedagogiczne, 1990 (Encyklopedia szkolna), s. 35, ISBN 83-02-02551-8.
- ↑ a b Eric W. Weisstein, Kite, [w:] MathWorld, Wolfram Research (ang.).
- ↑ Zydler, Jan: Geometria, red. nauk. Adela Świątek. Wydawnictwo Prószyński i S-ka, Warszawa 1997. ISBN 83-7180-155-6. Dostępna także tutaj.
- ↑ Geometria – Matematyka – Wirtualny Wszechświat. www.wiw.pl. [dostęp 2017-11-22].
- ↑ Reinhardt, Soeder: Atlas matematyki, Prószyński i S-ka Warszawa
- ↑ Bronsztejn, Siemiendiajew: Matematyka, poradnik encyklopedyczny, PWN Warszawa 1976
- ↑ deltoid, [w:] Encyklopedia PWN [dostęp 2008-01-07].
- ↑ Wybrane wzory matematyczne, Warszawa: Centralna Komisja Egzaminacyjna, 2015, s. 10, ISBN 978-83-940902-1-0.

