Rozkład geometryczny

Rozkład geometryczny
Funkcja rozkładu prawdopodobieństwa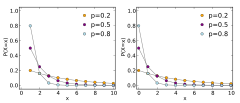
Dystrybuanta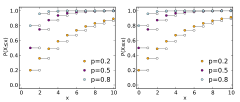
Parametry	$0<p\leq 1$ prawdopodobieństwo sukcesu (liczba rzeczywista)
Nośnik	$k\in \{1,2,3,\dots \}\!$
Funkcja rozkładu prawdopodobieństwa	$(1-p)^{k-1}\,p\!$
Dystrybuanta	$1-(1-p)^{k}\!$
Wartość oczekiwana (średnia)	${\frac {1}{p}}\!$
Mediana	$\left\lceil {\frac {-\log(2)}{\log(1-p)}}\right\rceil \!$ niejednoznaczna gdy $-\log(2)/\log(1-p)\in \mathbb {Z}$
Moda	$1\;$
Wariancja	${\frac {1-p}{p^{2}}}\!$
Współczynnik skośności	${\frac {2-p}{\sqrt {1-p}}}\!$
Kurtoza	$6+{\frac {p^{2}}{1-p}}\!$
Entropia	$-{\frac {1-p}{p}}\log _{2}(1-p)-\log _{2}p\!$
Funkcja tworząca momenty	${\frac {pe^{t}}{1-(1-p)e^{t}}}\!$
Funkcja charakterystyczna	${\frac {pe^{it}}{1-(1-p)\,e^{it}}}\!$
Odkrywca	William Feller (1950)

Rozkład geometryczny – dyskretny rozkład prawdopodobieństwa opisujący prawdopodobieństwo zdarzenia, że proces Bernoulliego odniesie pierwszy sukces dokładnie w k-tej próbie. k musi być liczbą naturalną dodatnią. Rozkład ten oznacza się zwykle symbolem Geo(p).

Zmienna losowa X ma więc rozkład Geo(p) jeśli

$P(X=k)=(1-p)^{k-1}p\,$

Zauważmy, że jeśli X ma rozkład Geo(p), to $P(X>k)=(1-p)^{k}$. Zatem jej dystrybuanta jest zadana wzorem $F_{X}(k)=P(X\leq k)=1-(1-p)^{k}$ dla liczb naturalnych k.

Uwaga: Niekiedy zamiast badać w której próbie odniesiemy pierwszy sukces, badamy ile prób z rzędu kończy się porażką. Wówczas tak zdefiniowane k jest o jeden mniejsze, więc we wszystkich wzorach należy dodać do niego 1.

Rozkład geometryczny to szczególny przypadek ujemnego rozkładu dwumianowego dla r = 1.

Ciągłym odpowiednikiem rozkładu geometrycznego jest rozkład wykładniczy.

Momenty

Funkcja tworząca prawdopodobieństwo zmiennej losowej X o rozkładzie Geo(p) jest zadana wzorem

$f(t)=\sum _{k=1}^{\infty }t^{k}(1-p)^{k-1}p={\frac {pt}{1-(1-p)t}}$

Z tego otrzymujemy

$\mathrm {E} (X)=f'(1)={\frac {p}{(1-(1-p)t)^{2}}}|_{t=1}={\frac {1}{p}}$

oraz

$\mathrm {E} (X(X-1))=f''(1)={\frac {2(1-p)}{p^{2}}}$

z czego otrzymujemy

$\mathrm {var} (X)=f''(1)+f'(1)-(f'(1))^{2}={\frac {2(1-p)}{p^{2}}}+{\frac {1}{p}}-{\frac {1}{p^{2}}}={\frac {1-p}{p^{2}}}$

Wyższe momenty główne $m_{k}$ rozkładów Geo(p) mogą być wyznaczone za pomocą funkcji generującej momenty. Spełniają one następującą zależność rekurencyjną:

$m_{k+1}=(1-p)\left(\left({\frac {1}{p}}+{\frac {1}{1-p}}\right)m_{k}-{\frac {dm_{k}}{dp}}\right)$

Momenty centalne $\mu _{a}$ rozkładów Geo(p) mogą być wyznaczone za pomocą funkcji generującej momenty centralne. Spełniają one następującą zależność rekurencyjną:

$\mu _{a+1}=(1-p)\left({\frac {a}{p^{2}}}\mu _{a-1}-{\frac {d\mu _{a}}{dp}}\right)$

Inne własności

Rozkład geometryczny jest bezpamięciowym: jeśli X ma rozkład Geo(p) i k, l są liczbami naturalnymi, to

$P(X>k+l|X>k)={\frac {P(X>k+l,X>k)}{(X>k)}}={\frac {P(X>k+l)}{(X>k)}}=$

${\frac {(1-p)^{k+l}}{(1-p)^{k}}}=(1-p)^{l}=P(X>l).$

Związki z innymi rozkładami

1. Jeśli $X_{1},\ldots ,X_{r}$ są niezależne i mają rozkład Geo(p), to ich suma $X_{1}+\ldots +X_{r}$ ma ujemny rozkład dwumianowy NB(r,p)
2. Jeśli $X_{1},\ldots ,X_{r}$ są niezależne i mają rozkład Geo(p) to zmienna losowa $Y=\min(X_{1},\ldots ,X_{r})$ ma rozkład geometryczny z parametrem $1-(1-p)^{r}$

Zobacz też

• rozkład hipergeometryczny